Линейная сложность последовательностей

Всякая конечная и периодическая бесконечная последовательности могут рассматриваться как ЛРП, вырабатываемая некоторым ЛРС. Поэтому некоторые свойства последовательности могут быть выражены через характеристики соответствующего ЛРС.

Пусть Р^т — векторное пространство размерности т над полем Р и X= {jf,}, i = 0, 1, … — последовательность над Р^т. Многочлен Р (Х) над полем Р, заданный (8.3), называется аннулирующим многочленом последовательности если верно рекуррентное соотношение.

при любом j > п, где и — нуль пространства Р^пг. Многочлен, ассоциированный с многочленом /(.г), также аннулирует последовательность XМножество всех аннулирующих многочленов последовательности Xобозначим Р_х_>[Х]. Минимальный многочлен последовательности X(обозначение ш_х^(Х)) — это ненулевой аннулирующий многочлен наименьшей степени.

Линейной сложностью или линейным размахом последовательности X (обозначение А (Х__>)) называют степень минимального многочлена т_х^(Х), г. е. А (Х__>) = degт_х_^(Х). Равносильным образом А (А'__>) определяется как порядок п самой короткой ЛРП, способной породить последовательность Xпри начальном векторе (х₀,…, х_п__х). Говоря нестрого, линейная сложность последовательности — это порядок «самого компактного» линейного рекуррентного закона, которому подчинены все знаки последовательности. Линейная сложность последовательности {и,…, и) любой дайны полагается равной 0.

Рассмотрим определяющие свойства линейной сложности последовательностей.

Теорема 8.9. Для любой последовательности Xнад Р^т:

• а) Р_х^[Х — идеал кольца Р[А,];
• б) т_х__>(Х) определен однозначно и делит любой многочлен f (x) е Р_х^[Х];
• в) если t — длина периода чисто периодической последовательности X то А/ — 1 е Р_х^Х.

М а) множество Р_х_>[Х] замкнуто относительно сложения и умножения на константы поля Р, иначе, если f (X), …,/.(X) е Р_х_>[А.], то рекуррентное соотношение (8.6) выполнено для любой линейной комбинации этих многочленов.

Если f (X) е Р_х^[Х], то (8.6) выполнено для многочлена f (X)X^f при любом t е N. Тогда f (X)g (X) е Р_х^[Х для любого g (X) е Р[Х] в силу замкнутости Р_х^[Х] относительно сложения и умножения на константы поля Р. Следовательно, Р_х^[Х] — идеал;

б) пусть т (Х) и р (Х) — различные минимальные многочлены последовательности Х_>, тогда ненулевой многочлен (т (X) — р (Х)) е Р_х^[Х] и имеет в силу унитарности многочленов т (X) и р (Х) степень меньше, чем degm (A.), что противоречит минимальности многочлена т (X).

Пусть т_х^(Х) не делит многочлен /(X) е Р_Х-> |Х|. Разделим f (X) на т_х_+(Х) с остатком: f (X) = m_x_>(X)q (X) + г (Х), где degr (X) < degw_x__>(X). По теореме 8.9а г (Х) е Р_х_+Х], что противоречит минимальности многочлена т_х^(X);

в) если длина периода последовательности Xравна t, то для всех j > t выполнено рекуррентное соотношение Xj — Xj__t = и, т. е. (А/ - 1) е P_xJX}. ?

Следствие. т_х^(Х) делит X^е — 1 и не делит X^k — 1 при любом & < t. D>

Высокая линейная сложность последовательности не означает ее безусловную пригодность для криптографических приложений. Например, близкая к вырожденной последовательность вида (а, а, b) длины /, где a, b е Р^т, а Ф Ь, имеет линейный размах, равный либо / - 1 (если ar = b при некотором г е Р), либо /.

Для последовательностей над полем Р линейная сложность эффективно определяется с помощью алгоритма Берлекемпа — Месси. Суть алгоритма заключается в подборе подходящего минимального многочлена последовательности путем индуктивного построения ряда многочленов, каждый из которых учитывает закономерности в последовательности более полно, чем предыдущий многочлен. Построение минимального многочлена последовательности Х_>, который является последним в построенном ряду, требует порядка А²(Х_+) операций поля Р.

Сложность алгоритма Берлекемпа — Месси для случайных последовательностей характеризуется с помощью введенного в [23] понятия профиля линейной сложности последовательности. Профилем линейной сложности последовательности Xназывается последовательность {А/}, / > О, где А/ есть линейная сложность отрезка {х₀, …, X/}. Известно, что для случайной идеальной последовательности Xнад полем порядка k математическое ожидание линейной сложности А/ близко к / / 2, а дисперсия ограничена константой, значение которой убывает с ростом порядка поля. Для линейной сложности последовательностей верны свойства.

Утверждение 8.9. Если mj (X) — минимальный многочлен последовательности Xj_> над P^mXj = 1, г, и X= Х_х^ • … • Х_г_^_у то т_х^(Х) = HOK (/w_t(A,),…, т_у(к)).

Л В соответствии с теоремой 8.9а многочлен НОК(т_х(Х), …, т_г(Х)) аннулирует Xj_> при j = 1, …, г, и, следовательно, аннулирует XПоэтому ««*->(*•) IHOKKCA.),… т,(к)).

Если т_х_>(к) ф НОЩт^Х),т_у(к)), то один из многочленов т_{(Х),…, т,.(Х) не делит т_х^(Х). Пусть не делит т_Л(Х). Тогда, но теореме 8.9а т_х^(X) не аннулирует Х_{^> следовательно, не аннулирует Х_>, что противоречит его определению. ?

Утверждение 8.10. Пусть Х_{_>_у …, Х_г_> — последовательности над Р^т с минимальными многочленами т_Л(Х)> …, т,.(Х), Y= с_хХ_х_> + … + с, Х_г^ - последовательность с минимальным многочленом т_у^(Х), где с_{, …с,.еР {0}. Тогда т_у_+(Х) делит HOK (nii (X),…, m_r(X)). D>

Нижняя граница линейной сложности последовательности = X_t_> + + Х₂_> дана в [19]:

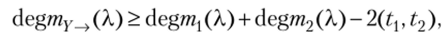
где t_x и t₂ — длины периодов последовательностей Х_х^ и Х₂_> соответственно. В частности, если (?_1? t₂) = 1 и (X — 1) I т_х(Х)т₂(Х), то degт_у^(Х) = degт_Л(Х) + + deg т₂(Х).

Если последовательность = {г/,} — почленное произведение последовательностей = {Xjj} над нолем Р [29], j = 1, г, т.с. г/, = x_n.jc_ir для i = О, 1, то Л (У_>) < Л (Х₁^)…Л (Х_Г^). Эта оценка достижима [4], если Р — поле простого порядка и т_л{Х), …, т_г(Х) — примитивные многочлены над Р попарно взаимно простых степеней.