Различимость состояний и входов

Одним из центральных вопросов теории конечных автоматов является минимизация автомата, точнее, для данного автомата, А возможность и сложность построения автомата В с меньшим внутренним алфавитом, реализующего то же множество автоматных отображений. В связи с этим важно сравнить поведение автомата в различных состояниях.

Реакцией состояния s (или автоматным отображением при начальном состоянии s или реакцией и.а. A_s) называется порожденное состоянием s отображение f_s: X* —> У*, где/₅(да) = f*(s, w). Реакция состояния s автономного автомата есть соответствующая состоянию s выходная последовательность. Реакция автомата А (или множество автоматных отображений), обозначаемая [Л] — это множество реакций всех состояний автомата: [А] = [fs е 5}.

Состояния s и z из S эквивалентны (k-эквивалентны), если одинаковы их реакции (па любое слово w е Х^к). Данные отношения рефлексивны, симметричны и транзитивны.

Автоматы Мили эквивалентны, если одинаковы их реакции. Эквивалентные автоматы Мили однородны: из равенства отображений следует совпадение областей определения и областей значений. Автомат Мили А называется сокращенным, если не эквивалентны любые два его состояния.

Наличие сокращенного автомата для данного автомата определяет следующая теорема.

Теорема 9.2 (Хаффман — Мили). Если sп> 1, то для эквивалентности состояний автомата Мили достаточно, чтобы совпали их реакции на входные слова длины не более п — 1.

Ч Обозначим через R_k разбиение множества S на классы^{-эквивалентных} состояний и через Ъ,_к — число блоков в разбиении R_k, k = 1,2,… В силу определения (k + 1^{эквивалентные} состояния являются и^{-эквивалентными.} Следовательно, каждый класс (k + 1)-эквивалентности целиком содержится в некотором классе^{-эквивалентности} и разбиение R_k+X является продолжением разбиения R_k.

Утверждение 9.1 (промежуточное). Если R_k+X = R_k, то = R_k для всех j > k, т. е.^{-эквивалентные} состояния просто эквивалентны.

А Достаточно показать для i > k, что из R= R_M следует R_i+X = R_i+2. Если состояния 5 и г автомата (г + 1)-эквивалентны, то fs, xzv) = f*(z_y xw) для всех х е X w we X. Отсюда, используя определение отображения /*, имеем: f (s_y x) f*(h (s, x), w) = f (z, x)f*(h (z, x)_yw). Это равенство равносильно двум следующим:

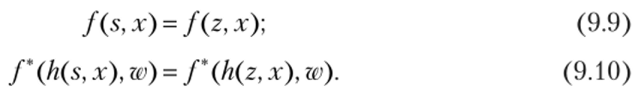
Из равенства (9.10) имеем, что /-эквивалентны состояния h (s, x) и h (z_yx). Но поскольку Rj = i?,₊₁, то эти состояния (/ + 1)-эквивалентны, тогда f*(h (s, х), *ш) = f*(h (z, х), гш) для всех х_у а е X и е X. Из последнего равенства и равенства (9.9) следует: /(5, x)f*(h (s, х), гга) = /(2, x)f*(h (z_y х), гш). Значит, состояния 5 и 2 автомата (/' + 2)-эквивалентны, т. е. /?_/+1 = Д_/+2.? Утверждение 9.2 (промежуточное). Если Rj Ф R_i+{y то ^ > /, i = 1, 2,…

^ (Индукция по /). Пусть г = 1 и R_x Ф R₂. Если ^ = 1, то любые состояния 5 и 2 автомата 1-эквивалентные, в том числе состояния h (s_y х) и h (z_y х) при любомхg X. Значит, при любыхx_ywe Xверны формулы (9.9) и (9.10), и состояния s и 2 автомата 2-эквивалентны по теореме 9.1. Отсюда R_{ = R₂, что противоречит условиям. Следовательно, > 1 и для i = 1 доказано.

Пусть утверждение доказано для i = k_y и /?*₊₁ * Т?_А,₊₂. Из последнего неравенства следуют неравенства /?, Ф R_M для / = 1, …, k_y противное противоречит утверждению 9.1. По предположению индукции это значит, что > i для всех i = 1,…, k. Если ?_{к+{ y}Tok_к< ^₊₁ < k + 1, отсюда ^ = ?*₊₁ = = А + 1, что противоречит условию ^ R_k+Xy значит, ^₊₁ > k + 1. ?

Для автомата А с п состояниями R_я-1 = R_n, иначе из утверждения 9.2 имеем > п — 1, т. е. = и = так как в R_n нс более п классов. Отсюда и из утверждения 9.1 получаем, что (п — 1^{эквивалентные} состояния являются просто эквивалентными. ?

Замечание. Для распознавания эквивалентности состояний автомата Мили с п состояниями значение достаточной длины слов, равное п — 1, неулучшаемо. О.

Следствие 1. Проблема эквивалентности состояний автомата Мили алгоритмически разрешима. D>

Следствие 2. Автоматы Мили Ли В соответственно спит состояниями эквивалентны, если совпадают их реакции на все входные слова длины, не большей п -г т — 1. Вследствие этого проблема эквивалентности автоматов Мили алгоритмически разрешима.

А Эквивалентные автоматы однородны, тогда положим А = (X, S, У, h,/), В = (X, S', У, h/'), где 5п5^,= 0. Рассмотрим автомат С = А и В. Для распознавания эквивалентности автоматов А и В достаточно показать, что для каждого состояния se S автомата А в автомате В найдется эквивалентное состояние s' е S', и наоборот. Следовательно, задача свелась к распознаванию эквивалентности состояний автомата С. По теореме 9.2 для этого достаточно рассмотреть входные последовательности длины, не большей п + т — 1. ?

Замечание. Значение достаточной длины слов, равное п + т- 1, неулучшаемо. >

Теорема 9.3 (о сокращении). Для каждого автомата Мили может быть эффективно построен эквивалентный сокращенный автомат.

А Сокращенный автомат строится из исходного автомата объединением всех эквивалентных состояний исходного автомата и отождествлением этого класса с состоянием сокращенного автомата. Действие функций переходов и выходов на классах совпадает с действием функций исходного автомата на любых представителях классов. По теореме 9.2 построение выполнимо за конечное число шагов. ?

Для некоторых приложений важна способность конечного автомата отображать различные входные слова в различные выходные слова. Входные слова v, w е X* неразличимы автоматом А (для автомата А), если f*(s, vu) = = f*(s, wu) для любого s е S и любого и е X*. В противном случае v и w различимы автоматом А. В частности, входные слова различных длин различимы автоматом Мили. Автомат А различает входы, если любые два различных входных слова различимы автоматом А.

Лемма 9.1. Входные слова v и w неразличимы автоматом А для любого s е S состояния ks, v) и ks, w) эквивалентны, и fs, v) = fs, w).

Ч Пусть входные слова v и w неразличимы автоматом А, и s любое. Тогда для всех и g X* справедливо: fs, v) fhs, v), и) = f*(s, vu) = f*(s, wu) = = fs, w) f*(h*(s, w), и). Отсюда имеем требуемое равенство, и состояния h*(s, v) и h*(s, w) эквивалентны.

Обратное утверждение доказывается аналогично. ?

Теорема 9.4 (Чен). Если S = п > 1, и любые два входных слова длины п^2п — 1 различимы автоматом А, то автомат А различает входы.

Следствие. Проблема распознавания различимости входов автоматом Мили алгоритмически разрешима. О.