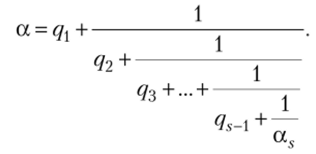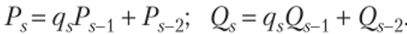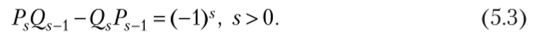Непрерывные дроби. 
Криптографические методы защиты информации. 
Часть 1. Математические аспекты

Пусть, а е R и q_{ = |а|, тогда при нецелом, а имеем: а = q_x + 1 / а₂, где а₂ > 1. Точно так же при нецелых а₂, а₅₋₁ имеем: а₂ = q₂ + 1 / а₃, а₃ > 1;… a,_i = + 1 / a_sf a_s > 1. Отсюда получаем разложение в непрерывную дробь:

Если, а иррациональное, то и а₅ иррациональное при любом 5, и процесс построения непрерывной дроби может быть неограниченно продолжен. Если же, а рациональное, а = а / Ь_} то данный процесс конечен и может быть выполнен с помощью алгоритма Евклида. Действительно,.

Тогда а / b = q_{ + а /b = q_x ±— -. Числа q_x> q₂называются.

^.

?з +••• +—.

Чп

• 1
• (как в алгоритме Евклида) неполнъши частными, а дроби 5₉ = q_{ + —,

Ч2

• 1
• 5₃= ц_х ±—,… называются подходящими дробями.

q₂+ —

Чз

Числители и знаменатели подходящих дробей образуются по рекур;

q jР 1.

рентному закону. Полагая Р₀= 1, Qn = 0, имеем: 5″ = — = —, б₂ = q_x + — =.

1 Qt Ч2

= ^{r/2 = ^Pl+P° =, 83= + _{= =}1_{ивобщем}}

2-l + 0 <7₂Qi⁺Qo Qi (^ch⁺1 / .

случае 5_V = ^^s^^s~^{l +} ^^s~² = —. Значит,.

<7,Q,-i+Q,-2 Qe.

Вычисление есть процесс заполнения таблицы, заполненной частично:

Последние два столбца пишутся, лишь когда, а — несократимая дробь а / b и Ъ > 0.

Пример 5.2. Вычисление подходящих дробей Разложим число 105/38. Алгоритм Евклида дает ряд неполных частных: q_{ = 2, q₂ = 1, 4 = 4, <7₅ = 2. Тогда заполняем таблицу, сначала q_b q₂, <73, <74, <75, Pq> Qo> затем Pj, Q|, затем Р₂, Q₂, ^{и Т}-Л;

Получаем подходящие дроби 6, = 2 /1, б₂ = 3 / 1,6₃ = 11 / 4, б₄ = 47 /17, б₅ = 105 / 38. D>

Р Р

Рассмотрим разность соседних подходящих дробей: 8_S — 5_S__X = ——-— =.

Q.s Qs-i.

= —-—, где A_s= P_SQ_S_ 1 — Q_sP_s-_i. Подставляя вместо P_s и Q_s. их выражение QsQs-1.

из рекуррентных формул и упрощая, получаем: h_s = -h_s__х. Поскольку h_{ = = q_l ? 0 — 1 • 1 = -1, то h_s = (-l)^s. Тогда.

Отсюда (при s = п) получаем, что в соответствии с расширенным алго;

(-1)'.

ритмом Евклида подходящие дроби несократимы и 8″. — 8^ =-, s > 1.

QsQs-i.

Заметим, что I, а — 8_Л_, | <-и, а лежат между 8_s_j и 8_Ч. (одно из чисел.

QsQs-i

больше а, другое — меньше).