Элементы теории вероятностей и математической статистики

Предметом математической науки — теории вероятностей — являются закономерности сложных явлений, характеризующие случайные (заранее точно не известно, какие) события и величины. При этом под случайным событием подразумевается возникновение такого специфического набора обстоятельств, который в конкретном случае может произойти или не произойти; под случайной величиной — переменная, способная принимать любое значение из области, определенной распределением соответствующих вероятностей; под вероятностью — действительное число в интервале от 0 до 1, относящееся к случайному событию и отражающее меру возможности его наступления или степень соответствующей субъективной уверенности.

Среди случайных событий выделяют: а) практически достоверные, вероятность которых весьма близка единице; б) практически невозможные, если их вероятность близка нулю; в) независимые, когда появление одного из событий не изменяет вероятности возникновения других; г) противоположные, если одно из двух событий обязательно произойдет в данном случае; д) совместные и несовместные, когда для первых возможно одновременное появление в конкретных условиях, а для вторых это исключено. Что касается случайных величин, то их принято делить на дискретные (способные принимать только целочисленные значения) и непрерывные — с любыми значениями из некоторого конечного или бесконечного интервала.

В основе теории вероятностей лежат три аксиомы, определяющие значения вероятности Р (*) появления случайного события (*), а также ее соотношения для противоположных событий и произведения двух совместных:

1) вероятность появления случайного события X представляет собой действительное число, удовлетворяющее следующим условиям:

2) вероятность невозникновения (обозначается X) случайного события X равна дополнению до единицы вероятности его возникновения —.

3) вероятность P (XY) одновременного появления совместных случайных событий X и Y равна произведению вероятности одного на условную (обозначают */*, понимая под звездочками буквенные коды соответствующих событий) вероятность другого —.

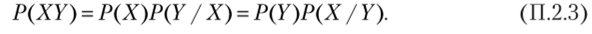
Случайная величина считается заданной, если известен закон ее распределения, под которым понимают соотношение, устанавливающее связь между возможными значениями случайной величины X_i и соответствующими вероятностями Р_г Известны три формы представления подобного закона.

1. Таблично-графическая — в вид о ряда распределения и соответствующего ему многоугольника, пример которых приведен на рис. П. 2.1.

Рис. П. 2.1. Пример ряда (а) и многоугольника (б) распределения.

2. Функция распределения F (x), называемая интегральным законом и численно равная вероятности того, что случайная величина X может быть меньше или равной ее конкретному значению хг.

Данная функция является универсальной характеристикой случайной величины, так как: а) существует для двух ее типов — дискретных и непрерывных; б) может задаваться графически (рис. П. 2.2, а); в) обладает следующими важными свойствами:

• • является неубывающей функцией своего аргумента, т. е. для любых х₂ > х_х справедливо неравенство F (x₂) > F (xi);
• • для х, равной минус бесконечности, данная функция равна нулю — F (-oo) = 0;
• • для x_t равной плюс бесконечности, эта функция равна единице — ?F (+°°) = 1;
• • вероятность попадания случайной величины на отрезок Ах = х₂ — х_{ равна

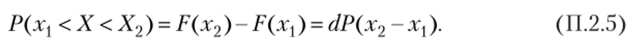
3. Плотность распределения (вероятностей), являющаяся первой производной (если существует) от функции распределения случайной величины:

Эту плотность также называют дифференциальным законом распределения, а связи между Р (х), F (x) и /(х) имеют следующий вид:

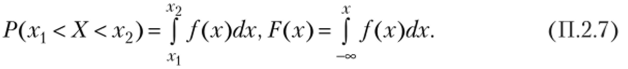
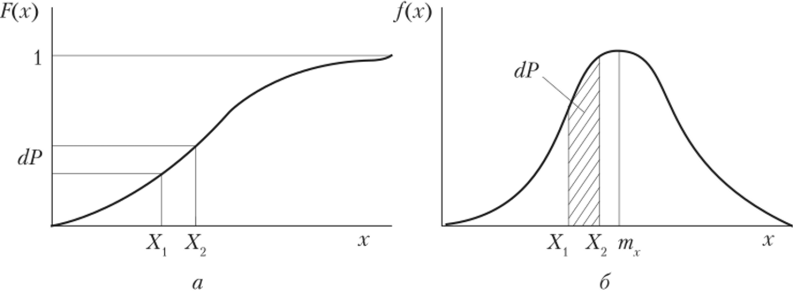
Рис. П. 2.2. Графики функции (а) и плотности (б) распределения Данный способ задания случайной величины обладает другими важными свойствами (часть из которых наглядно подтверждается рис. П. 2.2, б):

• а) плотность вероятности является неотрицательной функцией — f (x) > 0;
• б) определенный интеграл в бесконечных пределах от /(х) равен единице, что означает также равенство этой величине всей площади под ее графиком.

Помимо законов задания случайной величины широко применяются их числовые значения, характеризующие среднеориентировочное значение, разброс относительно него и другие свойства распределения случайной величины. При этом самым важным таким параметром является математическое ожидание, рассчитываемое по следующим формулам:

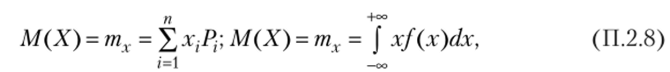
где Pj, f (x) — вероятности принятия конкретных значений х_{ дискретной случайной величиной X и плотность вероятности — непрерывной.

Второй полезной для практики числовой характеристикой случайной величины служит ее дисперсия, которая имеет следующий вид:

Что касается математической статистики, то ее предметом служат эмпирические количественные данные о массовых случайных явлениях, рассматриваемых теорией вероятностей, а методами — такие регистрация, описание, анализ и интерпретация этих сведений, которые отражают их реальные закономерности. Ее основными категориями считаются:

• • генеральная совокупность — множество всех реально известных предметов какого-либо типа;
• • выборка — часть генеральной совокупности, на основе изучения которой получают суждения, но всему множеству предметов;

• • оценивание — определение по выборке числовых значений (оценок) параметров распределения предметов, относящихся ко всей генеральной совокупности;
• • статистика — функция, полученная, но выборочным данным.

При оценивании числовых характеристик требуется, чтобы выборка была репрезентативной (представительной), т. е. обладала признаками, присущими всей генеральной совокупности, а оценка — удовлетворяла требованиям состоятельности. Последнее означает: а) отсутствие разницы между истинным значением искомого параметра и математическим ожиданием сто оценки; б) минимальную величину дисперсии такой оценки, что обеспечивает их сходимость по вероятности при росте объема выборки.

В основе процедуры статистического оценивания лежит так называемый закон больших чисел, представляющий собой две теоремы:

• 1) теорему Чебышева, утверждающую, что при неограниченном увеличении числа испытаний, являющихся независимыми, равноточными и свободными от систематических ошибок, среднее арифметическое от результатов измерения их параметров стремится по вероятности к математическому ожиданию измеряемой величины;
• 2) теорему Бернулли, являющуюся частным случаем предыдущей и констатирующую, что частота наблюдений случайного события стремится в аналогичных условиях к вероятности его возникновения.

В целом закон больших чисел является аксиоматикой математической статистики, закладывающей основу для интерпретации выборочного среднеарифметического математическим ожиданием случайной величины, а частоты появления случайных событий — их вероятностью.

Что касается основных задач математической статистики и распространенных способов их решения, то с определенной условностью все они могут быть разделены на следующие три группы:

• 1) оценивание параметров (числовых характеристик) предполагаемого закона распределения конкретной случайной величины. Данная задача решается при допущении о соответствии эмпирического распределения одному из известных статистических (нормальному, равномерному, экспоненциальному и т. д.), а ее примером можно считать оценивание математического ожидания и дисперсии случайной величины;
• 2) определение закона распределения случайной величины по совокупности ее эмпирических данных. Эта задача часто решается выравниванием или сглаживанием построенной с их помощью ломаной кривой (например, той, которая показана на рис. П. 2.1, б). На практике наиболее часто это достигается ее аппроксимацией одним из известных статистических распределений или аналитической зависимостью, называемой регрессией и представляющей собой алгебраический многочлен, удобный для описания параметров соответствующего явления;
• 3) проверка статистических гипотез (предположений) относительно характера распределения случайной величины или соотношения между ее параметрами и какими-то другими числовыми характеристиками. Данная задача связана с двумя предыдущими — как по причинам появления (ограниченность имеющихся статистических данных и ошибки в их значениях),

так и, но прикладной ценности (систематизирует имеющуюся информацию и повышает достоверность полученного на ее основе результата). Чаще всего она решается путем проверки возможности а) аппроксимировать какой-либо эмпирический график одним из известных теоретических распределений, 6) считать равными однотипные числовые характеристики, полученные на основе фиксированных выборочных данных на разных объектах или на одном и том же, но в разые моменты времени.