Спрос и теория потребительского выбора

Основой поведения потребителей является уже упоминавшаяся нами полезность потребления. При этом принято различать предельную и общую полезность.

Предельная полезность (MU — Marginal Utility) есть та полезность, которую потребитель извлекает из очередной дополнительной единицы блага.

Сумма предельных полезностей дает общую полезность (TU— Total Utility):

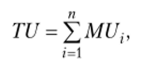
где MUi — предельная полезность потребления i-й единицы блага:

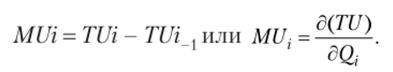
Если речь идет о наборе потребительских товаров, то предельная полезность товара может быть рассчитана как частная производная от функции общей полезности товарного набора по объему потребления i-го товара:

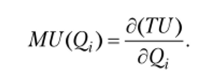
Характеризуя функцию общей полезности, необходимо отметить следующие ее свойства.

Функция общей полезности имеет возрастающий характер, т. е. каждая дополнительная единица блага увеличивает общую полезность (до некоторой точки насыщения).

Па рис. 1.12 приведены функции общей и предельной полезности. Каждая следующая единица блага приносит меньшее увеличение общей полезности, чем предыдущая (см. заштрихованные области на рис. 1.12). Иными словами, по мере увеличения количества потребляемого блага его предельная полезность имеет тенденцию к уменьшению (закон убывающей предельной полезности)^[1].

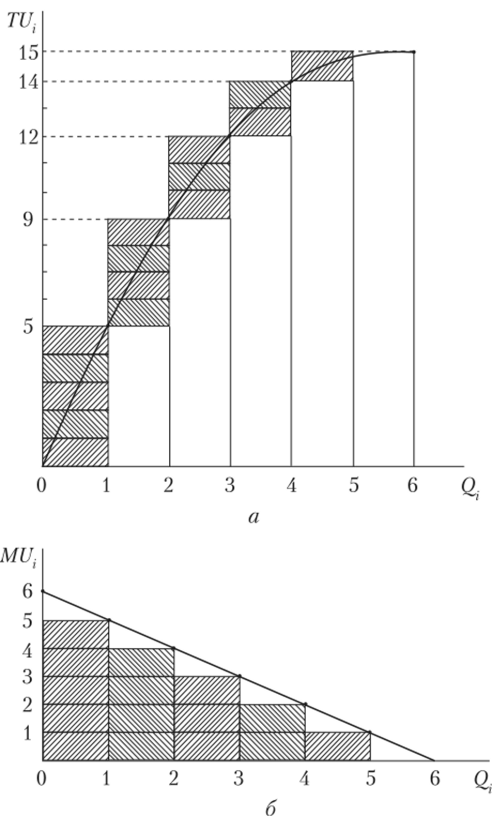
Рис. 1.12. Функции общей (а) и предельной (б) полезностей.

Анализируя графические модели функций общей и предельной полезностей, нетрудно убедиться в следующем: если полезность выражать в денежных единицах, то линия предельной полезности есть не что иное, как линия функции спроса на данный товар.

Понятие предельной полезности позволяет дать наиболее глубокое объяснение закону спроса. Поскольку каждая последующая единица блага приносит все меньшую дополнительную (предельную) полезность, потребитель, оценивая ее в денежных единицах, склонен за дополнительную единицу блага платить меньшую цену. Иными словами, покупатель выражает желание увеличить объем спроса только при снижении цены. Именно поэтому кривая индивидуального спроса на товар имеет нисходящий характер (отрицательный наклон).

Попытаемся теперь ответить на вопрос: в каких объемах потребителю выгоднее приобретать интересующие его товары, если ему известны их предельные полезности? Содержательно задача определения оптимального объема покупок выглядит следующим образом: при фиксированной цене товаров (Р_}) и известной величине бюджетного ограничения (В) надо определить оптимальные объемы покупок (Qf^pt), при которых значение функции общей полезности максимально¹, а стоимость всех покупок не превышает бюджета:

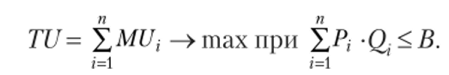
Решить данную экономико-математическую модель можно при помощи метода множителей Лагранжа^[2][3].

Условием экстремума целевой функции общей полезности в этом случае является равенство отношений:

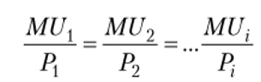
Отсюда следует, что товар пользуется повышенным спросом до тех пор, пока его предельная полезность, приходящаяся на одну затраченную денежную единицу, не становится равной предельной полезности других товаров на одну денежную единицу.

Иными словами: потребитель может максимизировать полезность, разделив свой бюджет так, чтобы последний рубль, израсходованный на приобретение каждого вида товаров, приносил бы одинаковое количество добавленной, или предельной, полезности (второй закон Госсена).

Рассмотренный кардиналистский подход к оптимизации поведения потребителя основывается на предположении возможности количественного измерения полезности. Но большинство экономистов считает, что потребитель не может с точностью сказать, сколько единиц полезности он получил от того или иного набора товаров, т. е. данное предположение является нереалистичным.

Поэтому в противоположность кардиналистскому был выдвинут ординалистский (порядковый) подход, не предполагающий необходимости количественного измерения полезности. Этот подход основан на возможности сравнения и упорядочения потребительских предпочтений (больше, меньше, равно). Вопрос о том, на сколько каких-либо единиц полезности один товар или набор товаров предпочтительнее другого, в данном случае не ставится. Таким образом, задача максимизации полезности сводится здесь к задаче выбора потребителем наиболее предпочтительного товара (набора товаров), доступного для него.

Система вкусов и предпочтений потребителя двух товаров может быть представлена на плоскости наглядно в виде кривой безразличия (рис. 1.13). Кривая безразличия (U) — линия, каждая точка которой представляет собой такую комбинацию двух товаров, что потребителю безразлично, какую из них выбирать. Кривая безразличия является нисходящей. Это означает, что если объем одного товара в наборе увеличивается, то объем другого товара будет сокращаться.

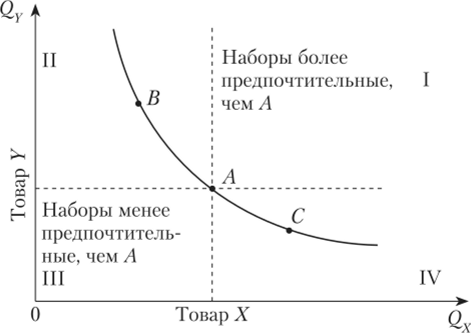
Рис. 1.13. Определение кривой безразличия.

Чтобы описать предпочтения потребителя по всем возможным наборам товаров X и Y, необходимо представить семейство кривых безразличия, которое иногда называют картой безразличия. Каждая кривая безразличия показывает в этом случае наборы товаров, к которым потребитель относится одинаково. В то же время каждая кривая безразличия соответствует определенной величине общей полезности. Очевидно, что кривые безразличия не могут пересечься.

Кривая безразличия отражает все возможные компромиссы при выборе потребителем того или иного набора товаров (рис. 1.14).

Из приведенной графической модели следует: чем большим количеством одного товара (например, X) потребитель располагает, тем меньшим количеством другого товара (в нашем случае У) он готов пожертвовать,.

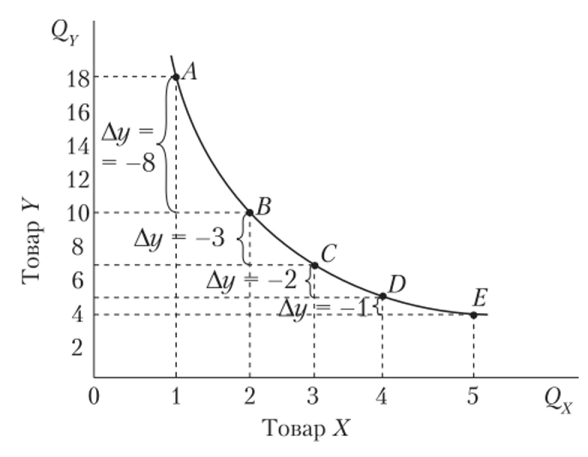
Рис. 1.14. Выбор набора товаров на кривой безразличия.

чтобы получить товара X еще больше. Эта модель отражает, таким образом, тот очевидный факт, что большинство потребителей получают все меньше и меньше удовлетворения по мере потребления все большего и большего количества любого товара. Наличие такой закономерности объясняет вогнутый характер кривой безразличия.

Чтобы количественно определить соответствующую степень компромисса, используется специальный показатель — предельная норма замещения (MRS — Marginal Rate of Substitution):

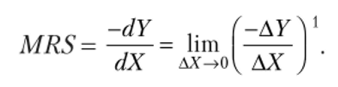
Предельную норму замещения можно связать с предельными полезностями экономических благ. Рассмотрим характер этой связи.

Изъятие AY единиц товара из набора наносит потребителю ущерб в AY • MU_Y единиц полезности. При замене товара Y соответствующим количеством (АХ) товара X приобретаемая полезность составит АХ • MU_X. Если потребитель при осуществленной замене экономического блага Y на товар X остается на той же самой кривой безразличия, то.

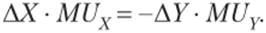
Следовательно,.

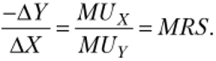
Итак, предельная норма замены товара Y на товар X может рассматриваться как отношение предельных полезностей товаров X и У.^[4]

Выбор количества каждого товара, приобретаемого за определенный период времени, зависит как от вкусов и предпочтений потребителя, которые описываются кривой безразличия, так и от экономических факторов, в частности цен товаров и доходов потребителя.

Множество доступных потребителю товарных наборов (область допустимых решений) с учетом цен и его доходов математически задается следующим образом:

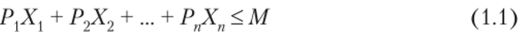
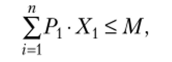
или где X_v X_v X_n — количество единиц товаров 1, 2, п, приобретаемых потребителем; P_v Р₂, Р_п — цены этих товаров; М — располагаемый доход потребителя.

Выражение (1.1) называется бюджетным ограничением, и для случая двух товаров (X и У) оно будет иметь следующий вид:

Линия, описываемая уравнением (1.2), называется бюджетной и характеризует все наборы товаров, которые может приобрести потребитель, полностью израсходовав свой доход М при данных ценах товаров X и У: Р_х и Р_у.

С учетом сказанного становится очевидным, что оптимальный (по критерию максимума общей полезности) набор потребительских товаров должен находиться на бюджетной линии. Проблема выбора оптимального решения сводится, следовательно, к выбору соответствующей точки на бюджетной линии.

В общем случае максимальная общая полезность при заданном бюджете достигается, когда потребляемая комбинация товаров соответствует точке, в которой бюджетная линия касается наивысшей из доступных кривой безразличия (рис. 1.15).

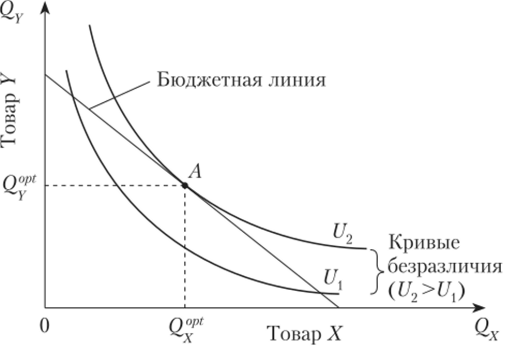
Рис. 1.15. Модель равновесия потребителя.

В точке А (см. рис. 1.15) бюджетная линия есть касательная к кривой безразличия U₂, следовательно, в точке А наклон бюджетной линии равен наклону кривой безразличия:

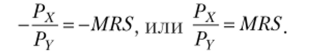
Таким образом, условие равновесия потребителя можно сформулировать как равенство предельной нормы замещения отношению цен товаров.

Предельная норма замещения показывает, в какой пропорции потребитель хочет заменить один товар (У) на другой (X), а отношение цен — в какой пропорции он может это сделать.

Легко убедиться, что условие равновесия потребителей в ординалистской теории эквивалентно соответствующему условию в кардиналистском варианте.

Так, ранее было показано, что.

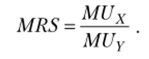
Принимая во внимание полученное выше равенство.

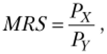
можно записать.

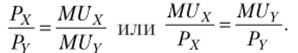
Для общего случая п благ (г = 1,…, п) получаем.

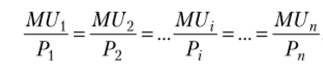
Эффекты дохода и замещения. Как следует из вышесказанного, изменение цены какого-либо товара оказывает соответствующее воздействие на объем спроса. Общий результат такого воздействия обусловлен действием двух факторов, или эффектов, — дохода и замещения.

Эффект дохода возникает, поскольку снижение цены конкретного товара увеличивает, а повышение цены уменьшает реальные доходы, или покупательную способность, потребителя.

При снижении цены некоторого товара потребители могут купить то же количество товара, потратив меньше денег, и таким образом у них остается больше средств для дополнительных покупок.

Эффект замещения проявляется, к примеру, в том, что у потребителя неизбежно возникает стимул приобрести дешевый товар вместо других товаров, ставших относительно первого дорогими. Потребители склонны заменять дорогие товары более дешевыми.

Эти два процесса обычно происходят одновременно, но для целей обоснования соответствующих управленческих решений будет полезно в нашем анализе провести между ними различия.

Рассмотрим графическую модель возникновения описанных выше эффектов дохода и замещения (рис. 1.16). В исходном положении в соответствии с определенным доходом М при ценах Р_х, P_Yтоваров X и Y бюджетная линия АВ будет иметь точку касания Е₀ с кривой безразличия U₀.

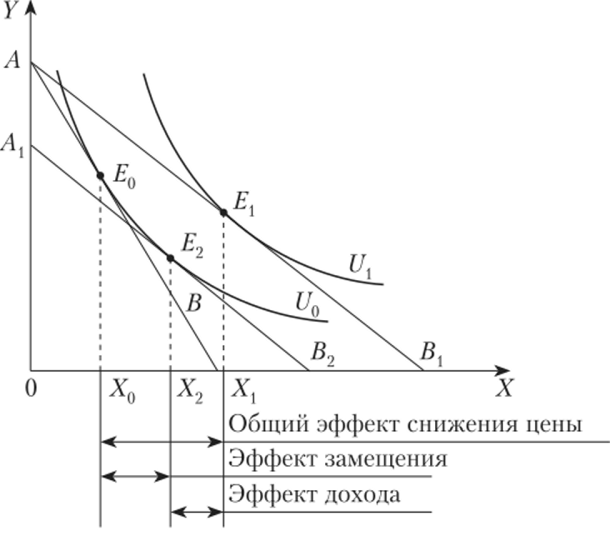
Рис. 1.16. Анализ эффекта изменения цены.

Предположим теперь, что цена товара X уменьшается. В этом случае бюджетная линия АВ начинает вращаться вокруг точки А против часовой стрелки и занимает положение АВ_{. В результате новая кривая безразличия U_{ имеет новую точку касания E_v представляющую собой новый оптимум потребления.

Таким образом, если раньше приобреталось Х₀ единиц товара X, то теперь данный товар приобретается в объеме Х_{ при общем эффекте снижения цены.

Далее определим эффект замещения, для которого характерно, что потребитель в условиях снизившейся цены товара X стремится при том же реальном доходе закупать больше данного товара.

Будем исходить из того, что степень удовлетворения потребителя остается неизменной, т. е. потребитель остается на той же кривой безразличия^[5]. Сначала определим, какими должны быть номинальные (денежные) доходы потребителя, чтобы при изменившемся соотношении цен обеспечить ему прежний уровень удовлетворения потребностей, соответствующий исходной кривой безразличия [/₀. Для этого параллельно линии АВ_Х проведем отражающую новое соотношение цен вспомогательную бюджетную линию А_{В₂ так, чтобы она касалась кривой безразличия U₀. Точка касания ?₉ характеризует объем Х₂ потребления товара X.

Обратите внимание: при переходе от первоначального Е₀ к дополнительному расчетному оптимуму Е₂ реальные доходы потребителя не меняются, а остаются на прежней кривой безразличия U₀.

Следовательно, сдвиг от Е₀ к Е₂ характеризует эффект замещения товара Y относительно подешевевшим товаром X. Его величина составляет (Х₂ — Х₀). Из вышесказанного следует, что собственно величина эффекта дохода составит (X_t — Х₂).

Следует также отметить, что эффект замещения при снижении цены товара всегда положителен. Действительно, принимая во внимание, что предельная норма замещения MRS равна отношению цен товаров P_x/P_Yi снижение цены Р_х будет означать уменьшение величины MRS. Следовательно, новая точка оптимума будет находиться правее и ниже исходной точки Е₀. Поэтому и точка Х₂ всегда будет находиться правее точки Х₀.

Что касается эффекта дохода, то он может быть и величиной отрицательной. Как следует из рис. 1.17, несмотря на отрицательную величину эффекта дохода, общий эффект от снижения цены товара X остался положительным. Однако вполне можно допустить, что отрицательный эффект дохода превысит эффект замещения. В итоге при снижении цены товара объем спроса на него надает. Закон спроса в этом случае «не работает», так как здесь мы имеем дело с товаром Гиффена (рис. 1.18).

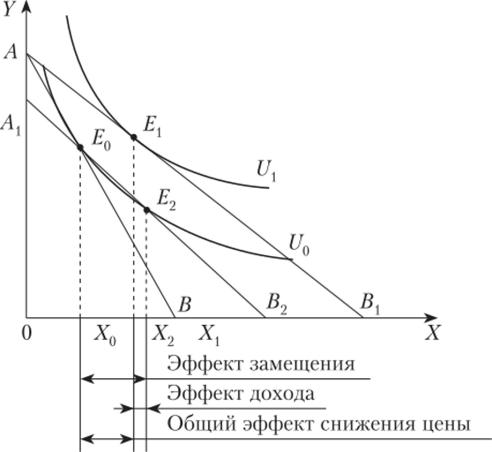
Рис. 1.17. Иллюстрация отрицательного эффекта дохода при общем положительном эффекте.

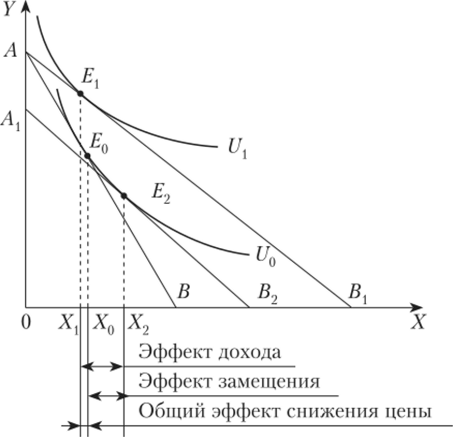
Рис. 1.18. Эффекты дохода и замещения для товара Гиффена.

Рассмотренный анализ выделения эффектов дохода и замещения в общем эффекте изменения цены товара может быть эффективно использован при моделировании поведения потребителей. Проиллюстрируем данное утверждение при помощи графической модели (рис. 1.19).

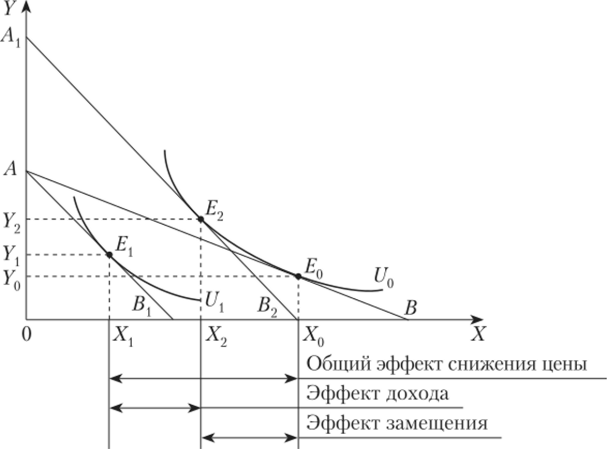
Рис. 1.19. Моделирование поведения потребителей.

Предположим, что исходное положение бюджетной линии — АВ, а точке потребительского оптимума (равновесия) Е₀ соответствуют значения Х₀ и У₀, где X — хлеб, Y — одежда.

В целях наиболее экономного расходования хлеба правительство решило повысить на него цены. В результате бюджетная линия займет другое положение, например АВ_{. Новая точка потребительского оптимума Е_{ будет в этом случае иметь координаты Х_х и Y_x. Закупки хлеба действительно уменьшатся, а покупки одежды возрастут.

Правительство, предвидя социальное недовольство в стране, ввело полную компенсацию за приобретаемый населением хлеб. В результате в новой ситуации бюджетная линия должна быть параллельна линии Л В, характеризуя тем самым прежнее соотношение цен между товарами X и У.

Точка равновесия потребителей Е₂ в окончательном варианте свидетельствует о том, что, несмотря на полную компенсацию подорожания хлеба, население снизило объемы его потребления, направив некоторую часть компенсации на приобретение одежды.

Итак, мы в очередной раз убедились в возможности эффективного использования экономической теории для обоснования конкретных управленческих решений теперь уже на макроуровне.

• [1] Данное положение имеет статус первого закона Госсена.
• [2] В этом заключается рациональное, или «разумное», поведение потребителя, из которого и исходит экономическая теория.
• [3] Лагранжиан этой модели имеет вид Условия оптимума выражаются системой откуда Итак, предельные полезности различных товаров в точке оптимума пропорциональныценам этих товаров. Это значит, что для любой пары товаров (i, j) отношение их предельныхполезностей равно отношению соответствующих цен: *2*3
• [4] Знак «минус» используется, чтобы предельная норма замещения была положительнымчислом, так как dY (AY) всегда отрицательные.
• [5] В экономической теории существуют два подхода к определению реального дохода, связанные с именами английского экономиста Дж. Хикса и русского математика Е. Е. Слуцкого. По Хиксу разные уровни денежных доходов, обеспечивающие один и тот же уровеньудовлетворения, т. е. позволяющие достигнуть одной и той же кривой безразличия, представляют собой одинаковый уровень реальных доходов. Согласно Слуцкому лишь тот уровень денежных доходов, который достаточен для приобретения одного и того же набора или комбинации товаров, обеспечивает неизменный уровень реальных доходов. Необходимо отмстить, что подход Хикса в большей мерс соответствует основным положениям порядковой (ординалистской) теории полезности, тогда как подход Слуцкогоколичественной (кардииалистской) теории полезности. Поэтому версия Хикса может бытьопределена как более общая.