Электрическое поле точечного заряда, расположенного около заземленной плоскости

Рассмотрим пример, когда применение теоремы единственности дает возможность найти простое решение одной сложной задачи электростатики. Точечный заряд Q находится на некотором расстоянии h от бесконечной проводящей плоскости (рис. 3.9). Пусть этот заряд будет положительным. Тогда на поверхности плоскости будет некоторым образом распределен индуцированный отрицательный заряд, возникающий из-за присутствия у поверхности заряда Q. Требуется найти электрическое поле, создаваемое этими зарядами.

Пусть потенциал р на плоскости всюду равен нулю. В реальных опытах этого можно достич, заземлив проводник, т. е. соединив его с землей. Потенциал в пространстве над плоскостью можно найти из уравнений Пуассона и Лапласа. Таким образом, пришли к граничной задаче, решение которой нельзя назвать очень простым. Однако существует очень простой метод решения подобных задач.

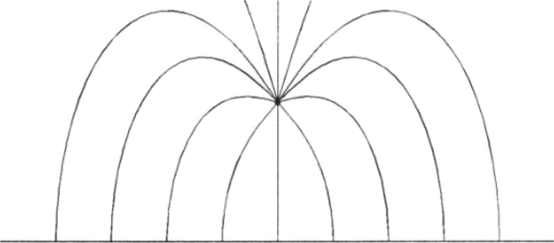
Рис. 3.9. Силовые линии электрического поля точечного заряда, расположенного над заземленной проводящей плоскостью.

Рассмотрим два заряда Q и —Q, расположенные на расстоянии 2/i один от другого (рис. 3.10). Пусть 5 — плоскость, которая проходит через середину отрезка, соединяющего заряды так, что он перпендикулярен к ней. Произвольная точка Р плоскости S находится на равных расстояниях от зарядов. Поэтому потенциал в любой точке этой плоскости равен нулю:

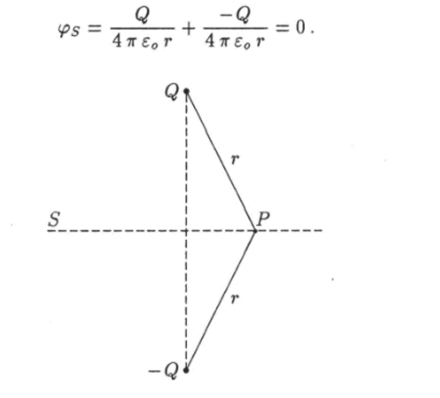
Рис. 3.10. Два заряда 104.

Таким образом, потенциал в полупространстве над плоскостью S удовлетворяет тем же граничным условиям, что в краевой задаче о поле, создаваемом зарядом Q, который расположен над заземленной проводящей плоскостью. В силу теоремы единственности электрическое поле, создаваемое двумя зарядами Q и — Q в в полупространстве над плоскостью S совпадает с полем, которое создает один заряд Q, расположенный над заземленной проводящей плоскостью.

Существуют системы зарядов, электрические поля которых очень просто рассчитать. К таким системам относятся системы, состоящие из небольшого числа точечных зарядов, и системы зарядов которые распределены в пространстве непрерывно и симметрично. Пусть для одной из таких систем найдено распределение потенциала в пространстве. Выделим одну из эквипотенциальных поверхностей 5. Пусть на этой поверхности потенцигит равен Заполним проводящей средой часть пространства, ограниченную поверхностью 5. Поверхность проводника является также эквипотенциальной. Если значение потенциала проводника равно , то электрическое поле в свободном от проводника пространстве будет таким же, каким оно было до его внесения.

Задача 1. Пространство между плоскостями х = — а и х = а заполнено однородным диэлектриком, диэлектрическая проницаемость которого равна е. В пространстве между плоскостями х = — а и i = О равномерно с плотностью д* распределен свободный заряд. Найти электрическую индукцию D, напряженность электрического поля Е, потенциал <�р, поляризованность Р, объемную д' и поверхностную <�т' плотности связанных зарядов.

Задача 2. Бесконечный цилиндр радиуса R, изготовленный из диэлектрика с проницаемостью е, заряжен равномерно по объему. При этом объемная плотность свободных зарядов равна д*. Найти электрическую индукцию D, напряженность электрического поля Е, потенциал <�р, поляризованность Р, объемную д' и поверхностную <�т' плотности связанных зарядов.

Задача 3. Шар радиуса Я, изготовленный из диэлектрика с проницаемостью е, заряжен равномерно по объему. Заряд шара равен Q. Найти энергию шара.

Задача 4. Цилиндрический конденсатор длиной /, радиусы обкладок которого равны, а и 6, заряжен до разности потенциалов U. Конденсатор заполнен веществом с проницаемостью е. Найти энергию, запасенную в конденсаторе.