Вопросы и задания для самоконтроля

РефератПомощь в написанииУзнать стоимостьмоей работы

Магнетизм — релятивистский эффект электричества Пусть по проводу движутся в разные стороны электроны и дырки (рис. 6.4). Движение электронов и дырок в разные стороны эквивалентно движению двух потоков электронов в одну сторону. То есть такое движение эквивалентно току, текущему по проводу. Пусть рядом с проводом движется заряженная частица. Тогда между движущимся зарядом и током будет иметь место… Читать ещё >

Вопросы и задания для самоконтроля (реферат, курсовая, диплом, контрольная)

Контрольные вопросы

6.1. На каких постулатах строится специальная теория относительности?
6.2. Каковы основные положения общей теории относительности?
6.3. Сформулируйте основные представления Максвелловской картины мира.
6.4. Как связаны свет и электромагнетизм?
6.5. Что общего и в чем различие между концепциями эфира и ноля?
6.6. В чем различие описания частиц и волн?
6.7. В чем заключается противоречивость описания света либо как волны, либо как потока частиц?

Кейсы

Кейс 6.1.

В чем причина разной скорости движения времени и разной длины предметов в движущейся и покоящейся системе?

Представим себе, что есть два перпендикулярных друг другу плоских мира А и В (рис. 6.1, а). Пусть вокруг оси 00, параллельной этим плоскостям, вращается стержень.

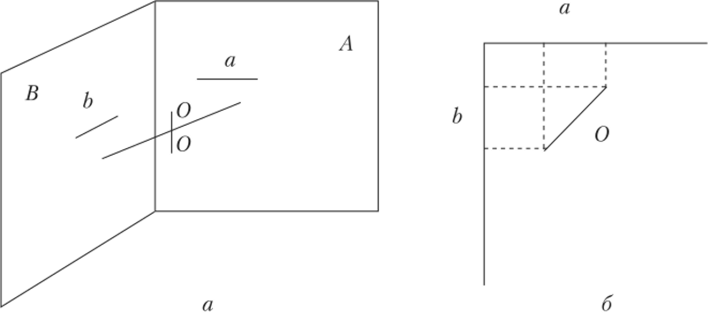
Рис. 6.1.

Тогда проекции а и b этого стержня на плоскости А и В соответственно будут меняться (рис. 6.1, б, вид сверху). Но жители мира А и В, общаясь друг с другом, будут удивлены, если обнаружат, что когда проекция а стержня в мире А увеличивается, то в мире В проекция b уменьшается, и наоборот. При этом жители обоих миров не знают, что они видят лишь проекции стержня, а не сам стержень. Со временем они догадаются, что мир не плоский, а трехмерный и длина стержня не меняется, а меняются лишь проекции этого стержня на плоскости А и В. Длину стержня в трехмерном мире / можно определить через проекции в мире А и В как.

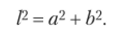
То есть в любой момент времени сумма квадратов проекций стержня остается постоянной.

Наш мир не трехмерный, а четырехмерный. Кроме трех пространственных координат есть четвертая — время. И длина четырехмерного отрезка (называемая интервалом) остается постоянной:

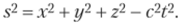
Четвертая координата — не просто время, а величина ict> где i — мнимая единица. Если в движущейся системе пространственные проекции уменьшаются, то временная проекция будет увеличиваться.

Задание. В четырехмерном пространстве задаются четырехмерные векторы, например, А^, где р = х_у г/, z, L Какие еще четырехмерные векторы вы знаете?

Кейс 6.2.

Релятивистское сокращение, замедление времени, сложение скоростей Пусть есть две инерциальные системы координат К и К' (рис. 6.2). Система К' движется вдоль оси К со скоростью и. Оси .г*, у и z системы К параллельны осям х', у' и z' системы К'.

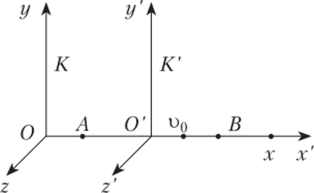
Рис. 6.2.

С помощью преобразования Лоренца устанавливается связь между координатами двух систем:

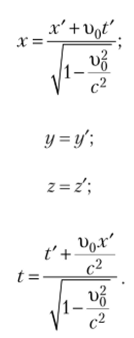
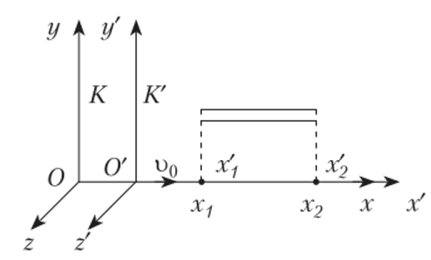
Рис. 63.

Преобразования Лоренца позволяют определить длину одного и того же тела в разных системах.

Пусть стержень будет расположен параллельно оси х^/ и покоиться относительно системы отсчета К' (рис. 6.3). Длина его в этой системе равна /₀ = х'₂ — х[, где координаты х[ и х₂ не меняются со временем tf. Относительно системы К стержень движется со скоростью в = % Для определения его длины в этой системе нужно отмстить координаты его концов х и х'₂ в системе К в одно и то же время t₀. Длина стержня в этой системе будетl = x₂-x_{. С помощью преобразования Лоренца выразим координаты х[ и х₂ через x_t и х₂:

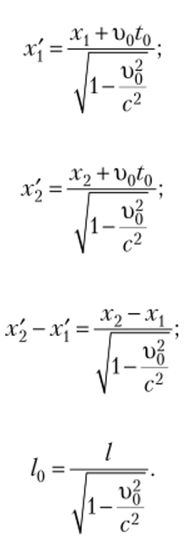
Тогда отношение длины стержня в системе К к длине стержня в системе К' будет следующим:

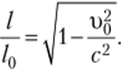
Размеры стержня вдоль осей у и у' и г и / одни и те же.

Используя преобразования Лоренца, можно узнать, как соотносятся промежутки времени в разных системах. Пусть в одной и той же точке х'₀ системы К' произошли два события в моменты времени t[ и t₂ . С помощью преобразования Лоренца выразим t[ и t₂ через t и t₂:

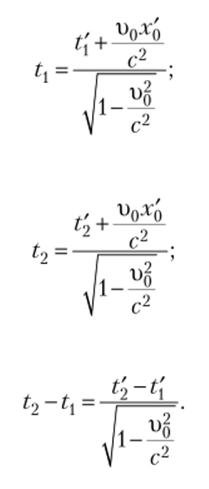
Введя обозначения t₂— t_{ = At t₂ -1[ = At получим формулу.

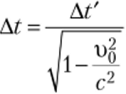
Отношение интервала времени At в системе К' к соответствующему интервалу времени At в системе К будет.

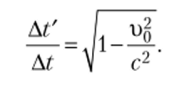
Используя преобразования Лоренца, можно решить задачу сложения скоростей. Допустим, есть неподвижная система координат К, в которой находится наблюдатель. Мимо него пролетает ракета со скоростью г>₀ (система К'), с ракеты запустили спасательную капсулу со скоростью и относительно ракеты. Какую скорость будет иметь эта капсула относительно системы К?

Из формул преобразования Лоренца можно записать дифференциалы координат в системе К через дифференциалы в К':

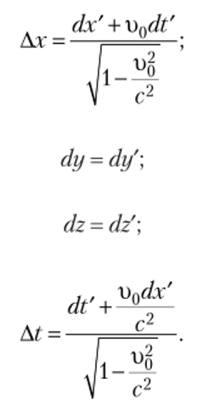
Разделив dx, dy и dz на dt, получим формулы преобразования компонент скоростей:

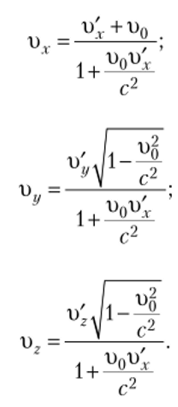
Если тело движется параллельно оси х, его скорость и относительно системы /С совпадает с, а скорость и' относительно системы К' — со скоростью слУ_х. В этом случае закон сложения скоростей будет выглядеть так:

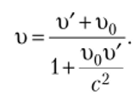
Задание. Где и как можно наблюдать на Земле релятивистское сокращение, замедление времени? Покажите, что если мимо неподвижного наблюдателя пролетает ракета со скоростью, близкой к скорости света, и в ней включили фонарик, свет которого будет распространяться в ту же сторону, что и движение ракеты, то для неподвижного наблюдателя, мимо которого пролетает ракета, скорость света фонарика равна с.

Кейс 6.3.

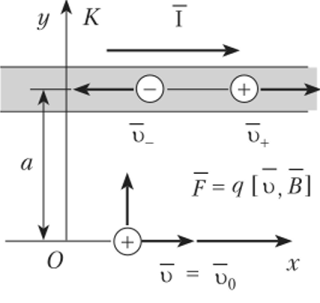
Рис. 6.4

Есть ли в данном случае электрическое взаимодействие между зарядами в проводе и движущимся отдельным зарядом?

Нет, электрического взаимодействия не будет: так как потоки электронов и дырок одинаковы, то, если взять какой-нибудь кусок провода, в каждый момент времени количество положительных зарядов будет равно количеству отрицательных. И полный заряд этого кусочка будет равен нулю.

Если мы перейдем в систему, которая будет двигаться с такой же скоростью, что и заряд, то в этой системе наш заряд будет покоиться. Тогда на него не будет магнитного воздействия. Но в новой системе координат, помимо того, что электроны и дырки продолжают двигаться в разные стороны, скорость дырок уменьшилась, а скорость электронов увеличилась.

В системах, движущихся с разными скоростями, следуя теории относительности, линейные размеры становятся разными. Л это значит, что если взять небольшой кусок провода, то теперь количество положительных и отрицательных зарядов будет разным. То есть провод становится заряженным, и теперь между проводом и зарядом будет электрическое взаимодействие (рис. 6.5).

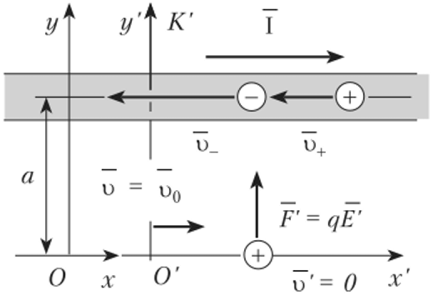
Рис. 6.5.

Задание. Какой вывод следует из описания этого эксперимента?

Насколько реальны электрические и магнитные поля?

Можно ли сделать вывод о том, что электрическое и магнитное взаимодействие есть составные части единого электромагнитного взаимодействия, порождаемого заряжен 11 ы м и частицам и ?

Кейс 6.4.

Масса в теории относительности В 1905 г. А. Эйнштейн установил связь между массой тела и содержащейся в нем энергией:

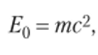
где Е₀ — энергия покоя; т — масса тела; с — скорость света.

Это, вне сомнения, одна из самых знаменитых формул теории относительности. Ей нашлось много практических применений, часть из которых были трагичными. По праву эту формулу можно считать визитной карточкой науки XX в.

Иногда в литературе можно встретить «массу покоя» /% но это излишняя величина. Вполне достаточно массы тела т: она одна и та же как в теории относительности, так и в механике Ньютона.

В ньютоновой механике:

• масса есть мера количества вещества;
• масса нескольких тел равна сумме масс этих тел;

• масса тела во всех инерциальных системах одна и та же;
• масса есть мера инертности тела.

Есть два соотношения, в которых масса т — мера инерции тела. В первом она связывает импульс тела р и его скорость о:

Во втором она связывает силу F, действующую на тело, и его ускорение а:

Соотношения (6.2) и (6.3) совместимы в ньютоновой механике. В ней действует принцип относительности Галилея, согласно которому при переходе от одной инерциальной системы к другой уравнения механики Ньютона не меняются:

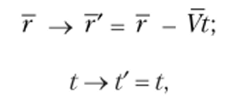
где 7 — радиус-вектор материальной точки в неподвижной системе; 7' — радиусвектор материальной точки в движущейся системе; V — скорость одной инерциальной системы относительно другой.

Б специальной теории относительности:

• масса не есть мера количества материи;
• масса системы частиц определяется их энергиями и взаимной ориентацией импульсов;
• масса составного тела не совпадает с суммой масс, составляющих его;
• в изолированной системе тел масса сохраняется со временем;
• масса тела в разных инерциальных системах отсчета одна и та же;
• при релятивистском движении масса тела нс есть мера его инертности.

Основными соотношениями специальной теории относительности для движущейся частицы являются:

где Е — энергия; р — импульс; т — масса; й — скорость частицы. Причем масса т и скорость о для частицы — это те же самые величины, что и в механике Ньютона.

Выше мы уже говорили о том, что энергия Е и импульс р, так же как t и 7, есть компоненты четырехмерного вектора. Они изменяются, если перейти от одной инерциальной системы к другой в соответствии с преобразованиями Лоренца. Что касается массы, то она при этом не изменяется, т. е. она есть лоренцевый инвариант, но уже обладает свойством аддитивности.

И еще, в отличие от классической механики, в релятивистской энергия тела не становится нулевой даже тогда, когда оно покоится, т. е. при о = 0 импульс р = 0. Так как Е₀ = тс², энергия покоя тела пропорциональна его массе. Это значит, что в покоящейся материи содержатся огромные запасы энергии, — и это главное практическое следствие теории относительности. На этом основываются вся ядерная энергетика и ядсрнос оружие. Вообщс-то, на этом же базируется и обычная энергетика.

При равенстве модуля скорости в = с из (6.5) следует, что Вопросы и задания для самоконтроля.

Если подставить равенство (6.6) в уравнение (6.4), мы получим, что масса такого тела должна равняться нулю. Или по-другому: нет такой системы координат, в которой тело покоится.

Для частиц с ненулевой массой, подставив формулу (6.5) в формулу (6.4), получим.

Извлекая квадратный корень из правой и левой части равенства, получим.

Если подставить (6.8) в (6.5), получим.

Из формул (6.8) и (6.9) следует, что тела с ненулевой массой нс могут достигать скорости света, так как при этом энергия и импульс тела обратятся в бесконечность.

Внимание! Не масса становится бесконечной — бесконечными становятся энергии и импульсы!

Согласно теории относительности, масса частицы — это мера энергии, содержащейся в покоящейся частице. В нерелятивистской механике об этом свойстве массы не знали.

При протекании ядерных или химических реакций разности масс частиц, участвующих в реакции, и масс продуктов реакции есть энергия, которая либо требуется для протекания реакции, либо выделяется в результате ее. Например, энергия фотона, рожденного в результате аннигиляции электрона и позитрона, равна энергии покоя электрона и позитрона. Относительное уменьшение массы при этом будет dm/m = 1.

При протекании на Солнце термоядерных реакций происходит превращение двух электронов и четырех протонов в ядро гелия и два нейтрино, при этом выделяется ?_кнн = 29,3 МэВ. Относительное уменьшение массы составляет dm/m = 0,8 • И)^-2.

В результате столкновения нейтрона с ядром урана ²³⁵U образуются два осколка и несколько нейтронов. При этом выделяется энергия ?_КИ|| = 200 МэВ. Относительное уменьшение массы составляет dm/m = 0,9 • 10~³.

При горении метана в конфорке кухонной газовой плиты, в результате реакции.

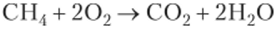
на кубический метр метана выделяется энергия, равная 35,6 МДж. Относительное уменьшение массы составляет dm/m = 10^_1().

При таянии льда изменение массы происходит на величину dm/m = 3,7 • 10^-12.

При нагреве металлической болванки до 200 °C ее масса возрастает на величину dm/m = 10-¹².

Задание. В литературе встречаются следующие формулы связи между энергией тела и его массой:

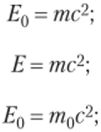
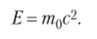
Здесь Е₀ — энергия покоя; т — масса тела; с — скорость света; Е — полная энергия тела; т₀ — масса покоя того же тела.

Как вы считаете, какая из этих формул верна? Обоснуйте свое решение.

Темы рефератов

6.1. Максвелловская (электромагнитная) картина мира.
6.2. Чем отличается макромир от мегамира?
6.3. История представлений о природе света.
6.4. Ядсрная энергетика и специальная теория относительности.

Вопросы и задания для самоконтроля (реферат, курсовая, диплом, контрольная)

Рекомендуемая литература