Оптимизации цепи поставок и ее решение

Окончательно, учитывая приведенные равенства (6.1) и (6.2), можно формализовать задачу оптимизации запасов с учетом ВЦД, а именно, опуская множитель (1 + гм/ 2), который не зависит ни от Г0, ни от q (, задачу минимизации суммарных издержек (приведенных к концу года с учетом ВЦД) формулируем как задачу определения такого интервала повторного заказа, при котором.

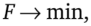
где.

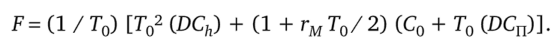
Анализируя последнее выражение для целевой функции F, легко видеть, что интересующая нас задача оптимизации эквивалентна задаче выбора длительности интервала повторного заказа, при которой минимизируется интенсивность денежного потока затрат (издержек). Понятно, что при этом условие целочисленности показателя 1 / Т₀ не требуется. Поэтому указанное ограничение можно далее не учитывать.

Отбрасывая слагаемые, которые не зависят от Т₀, получаем такой формат задачи оптимизации, который характерен для теории управления запасами. Это задача минимизация суммы двух слагаемых, когда одно из них является гиперболой, а второе — прямой линией, выходящей из начала координат:

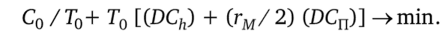
Напомним, что наилучшее решение для задач такого типа достигается в точке (обозначим ее Т_опт), где значения отмеченных двух типов слагаемых совпадают. Учитывая это, легко получить окончательный результат для Т_опт с учетом ВЦД:

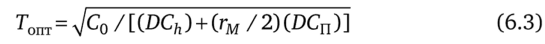
(доказательство опускается, чтобы не увеличивать объем работы).

Заметим, что в формате ситуации, когда оптимизация запасов выполняется без учета ВЦД, т. е. при г = 0, формула (6.3) примет вид.

Т₀ = yjc₀ / (DC/,). Кроме того, отметим, что традиционный формат такой формулы (применительно к модели без учета ВЦД, причем с оплатой только занятых мест на складе) в принятых здесь обозначениях дает известное равенство: Т₀ =^2С₀ /(DC_h). Как видим, полученная здесь для Г_опт формула (6.3) существенно отличается от хорошо известных традиционных формул для интервала повторного заказа Г₀, а именно указанные отличия формулы (6.3) характеризуются следующими особенностями.

• 1. Сравнивая с традиционным вариантом формулы для интервала повторного заказа, видно, что отсутствует цифра «2» в числителе под знаком квадратного корня (именно из-за того, что оплачиваются все арендованные места на складе, а не только те, которые будут фактически заняты).
• 2. Дополнительно, в отличие от традиционного формата такой формулы, присутствуют стоимости i-товаров. Действительно, они использованы в скалярном произведении (DC_n), которое находится в знаменателе подкоренного выражения. Соответственно, как видим, чем дороже будет товар, тем меньшим будет размер партии заказа и будут более частыми поставки.
• 3. Из-за учета концепции временной ценности денег в формуле (6.3) присутствует параметр г_м (в виде дроби г_м / 2) также в знаменателе подкоренного выражения; он характеризует эффективность денежных потоков в самой анализируемой цепи поставок (точнее, рентабельность используемого оборотного капитала для работы цепи поставок). Как видим, г_м является одним из атрибутов модели и не может задаваться извне.
• 4. Поскольку указанный показатель г_м является атрибутом самой цепи поставок, то его значение надо определять в формате оптимизируемой модели. Такая оценка будет предоставлена в параграфе 6.4. Кстати, обратим внимание на тот факт, что чем более эффективной будет цепь поставок, тем меньшим будет оптимальный размер партии заказа и тем более частыми будут поставки.