Учебные тексты, способствующие развитию визуального способа кодирования информации

Отмечая решающую роль слова в становлении мыслительной деятельности, нельзя забывать о том, что формирование понятийного мышления не сводится лишь к овладению языком. Превращение слова в действительный регулятор процесса усвоения информации предполагает определенный уровень организации чувственно-практического опыта учащегося, в частности, предметные действия и зрительные впечатления должны быть представлены в наглядно-обобщенной форме, обеспечивающей фиксацию существенных черт объекта.

Трудности мышления, оторванного от образной основы, вполне естественны: образ — это не просто «приложение» к теоретической (понятийной) мысли, это ее необходимая составная часть. Мышление, лишенное элементов образности, рискует стать сухим, бесплодным, формальным. Обучение, не обращенное к образному опыту, не только не способствует развитию понятийного мышления, но и, в конечном счете, подавляет его. Умение мобилизовать образное мышление при изучении математического материала облегчает его понимание и запоминание.

На основе результатов психологических исследований (Р. Арнхейм, Л. М. Беккер, В. П. Зинченко, Л. Ф. Обухова, М. А. Холодная, Н. И. Чуприкова, М. Н. Шардаков, И. С. Якиманская и др.) можно выделить специфику образного языка понятийной мысли. Перечислим некоторые существенные свойства образов, входящих в состав понятийной мысли:

• • динамичность — подвижность, активное преобразование образа, изменение исходного образа в соответствии с требованиями задачи, а также возможность развития образа в ходе мыслительной деятельности;
• • структурированность — дифференцированность и упорядоченность компонентов образа, выделение в нем деталей, характеризующих значимые свойства изучаемого объекта;
• • обобщенность — передача в образных формах наиболее общих и существенных закономерностей изучаемых явлений, выделение в образе частных и общих признаков объекта;
• • системность — соотнесение данного образа с рядом других образов.

Особое внимание развитию образного мышления традиционно уделяется при анализе процесса изучения школьного курса геометрии (В. А. Гусев, Е. Н. Кабанова-Меллер, М. В. Рычик, Г. И. Саранцев, О. В. Холодная, А. Я. Цукарь, И. С. Якиманская и др.). В арифметике и алгебре визуальный способ кодирования информации может сделать для учащихся «зримыми» слова и предложения математики, может послужить основой для введения нового понятия, может стать условием организации учебного материала и средством контроля мыслительной деятельности.

А. Белл описывает ситуацию, когда в начале урока на тему «Сложение десятичных дробей» учащимся было предложено выполнить следующее задание.

Заполните пропуски.

• 0,2; 0,4; 0,6; 0,8;…;…; (прибавляя по 0,2)
• 0,25; …;…;…; (прибавляя по 0,2).

Среди ответов учащихся появляются такие: «0,8 + 0,2 = 0,10», «0,25 + 0,2 = 0,27». Учитель не старается сразу исправить ошибки учащихся, а предлагает выполнить это же задание на числовом луче. Практически все школьники, допустившие ошибку, находят ее и принимают участие в поиске правила сложения десятичных дробей (Bell, 1998).

Образы позволяют обеспечить такую характеристику понятия, как его предметная отнесенность, сделать мыслительный процесс более ярким, гибким, повысить его эмоциональную насыщенность.

В исследовании Н. А. Резник рассматриваются различные аспекты развития визуального мышления. В частности, она указывает на роль «картинки» «как способа разъяснения изучаемого, как решение определенного вопроса, как макет для разрешения поисковой ситуации, как собирательный образ нескольких фактов учебной теории, как материал для формирования параллелей и аналогий» (Резник, 1999, с. 59).

Выделим учебные тексты, которые способствуют формированию нормативных образов как носителей определенного математического знания.

Под нормативными образами будем понимать те образы, которые выработаны и в истории математики, и в истории преподавания школьной математики (таблица разрядов, числовой луч, координатная прямая, графики функции, площадь прямоугольника, отрезок и др.).

Рассмотрим тип учебных текстов, получивших название «текст — формирование нормативного образа». Цель таких текстов — создание условий для выделения существенных свойств образов. Так, в рамках темы «Положительные и отрицательные числа» (5-й класс) учащимся предлагается текст, работа над которым поможет им развести общие и частные признаки понятия «координатная прямая».

Можно ли по данным рисункам определять координаты отмеченных точек? Если да, то укажите эти координаты.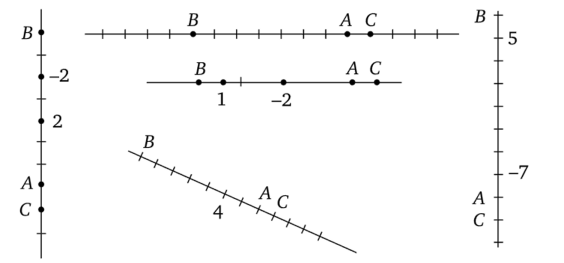

• 1. Пришлось ли вам ответить на следующие вопросы:
  • • Где на координатных прямых находится начало отсчета?
  • • Нужно ли указывать на них положительное направление?
  • • Почему они расположены по-разному?
  • • Какие координаты имеют точки А, В, С и чему равно расстояние между заданными точками в каждом случае?

Может быть, у вас появились свои вопросы?

2. Найдите допущенные на этом рисунке ошибки и исправьте их.

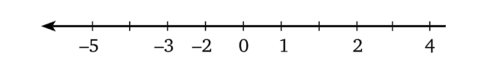
(Математика-5. Ч. 2. Положительные и отрицательные числа, 2005, с. 117—118.).

Это задание позволяет учащимся выделить с помощью слова существенные признаки координатной прямой, рассмотреть такие элементы этого образа, как «единичный отрезок», «начало отсчета», «положительное направление», а также гибко их использовать.

Результаты контрольных работ часто показывают, что образы учащихся, связанные с графиками функции, носят фрагментарный характер. Учащиеся не могут соотнести элементы графиков с поставленными задачами. Анализируя эти результаты, мы посчитали, что их причиной является недостаточная работа над структурой данного образа.

При этом мы опирались на исследования Е. Н. Кабановой-Меллер, посвященные выявлению тех мыслительных операций, которые влияют на формирование у учащихся образов, адекватных содержанию изучаемых понятий. В частности, она пишет: «Под структурой образа мы понимаем следующее: выражены ли в образе те существенные признаки предмета, которые сформулированы в определении понятия?» (Кабанова-Меллер, 1968, с. 95).

Приведем фрагмент текста, способствующего выделению свойств графика квадратичной функции (тема «Квадратичная функция», 9-й класс).

Верны ли следующие утверждения:

• 1. Вершиной графика функции у = (х — I)² является точка М (1; 0), а вершиной графика функции у = (х — 2)² — точка Р (—2; 0).
• 1 ₂ 1
• 2. Ось симметрии графика функции у =—(х-3) имеет уравнение х = — .
• 2 2
• 3. График функции у = —2(х — 4)² симметричен графику функции у = 2(х — 4)² относительно оси Ох.
• 4. Наименьшее значение функции у = —(х-2)² равно 0, и ветви параболы направлены вверх. ~
• (Квадратичная функция, 2001, с. 90.)

Для формирования образа квадратичной функции предлагаются задания, которые специально учат школьников выделять отдельные элементы графика квадратичной функции в зависимости от поставленной задачи, активно преобразовывать образ. Приведем примеры двух таких заданий.

Используя график функции, ответьте на вопросы.

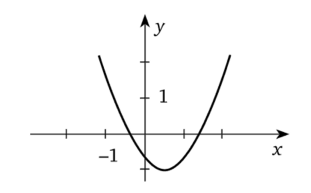
Верно ли, что:

• а) если* = 0, тоу = 0,75;
• б) еслих = 2, тоу > 0;
• в) еслих = 1, тоу > 0;
• г) еслих = 0, тоу < 0;
• д) еслих = 0,4, тоу > 0;
• е) еслих = 5, тоу < 0.
• (Квадратичная функция, 2001, с. 95.)

О параболе у = ах² + Ьх + с известно, что ее ветви направлены вверх, она не пересекает оси абсцисс, пересекает ось ординат в точке С (0; 7). (Приведите пример такой параболы.).

Что из этой информации кажется вам существенным для решения:

• 1) уравнения ах² + Ьх + с = 0;
• 2) неравенства ах² + Ьх + с > 0;
• 3) вопроса о наибольшем значении трехчлена ах² + Ьх + с?
• (Квадратичная функция, 2001, с. 161.)

Каждое из этих заданий создает условия для того, чтобы сформировать у учащихся умение выделять отдельные элементы образа в зависимости от поставленной задачи, что способствует развитию у учащихся умения использовать визуальный способ кодирования информации при решении задач.

Визуальный способ кодирования информации используется и развивается с помощью учебного материала, побуждающего школьников к развитию образа в ходе рассуждения, к его обобщению, перестройке в связи с возникающими проблемами. Тексты этого типа можно назвать «текст — развитие образа».

Рассмотрим тексты в рамках темы «Натуральные числа и десятичные дроби» (5-й класс), которые способствуют развитию такого образа, как «таблица разрядов». Таблица разрядов служит целям образного представления принципа десятичной нумерации натуральных чисел. При введении десятичных дробей эта таблица продолжается вправо разрядами, меньшими единицы, сохраняя тот же принцип поразрядного значения цифры.

Вот фрагмент текста, посредством которого обобщается известный учащимся образ таблицы разрядов.

В записи десятичных дробей целая часть отделяется от дробной части запятой. Например: 2,6; 0,5.

(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 62—63.).

Л. Ф. Обухова, анализируя работы Ж. Пиаже, отмечает, что он выделяет два типа образов: репродуктивные (воспроизводящие) и антиципирующие (предвосхищающие) образы (Обухова, 1981).

Мы рассчитываем на то, что новый образ таблицы разрядов станет помощником для построения учащимися гипотез о правилах действий над десятичными дробями, то есть выполнит функцию предвосхищения.

Е. Н. Кабанова-Меллер отмечает, что «роль образа в мышлении учащихся зависит не от конкретности или схематичности образа, а от других особенностей его структуры: насколько выражены в этом образе существенные признаки изучаемых явлений» (Кабанова-Меллер, 1968, с. 96).

Рассмотрим три вида текстов для учащихся 5-х классов, которые способствуют выделению существенных и несущественных свойств позиционной записи натуральных чисел с помощью таблицы разрядов. Учащиеся уже знакомы с десятичной системой счисления. В таблице разрядов «ряды» назывались «единицы», «десятки», «сотни» и т. д. Учащимся предлагается новая ситуация использования таблицы.

Самое интересное, что Муми-троллева таблица разрядов оказалась пригодной и для восьмеричной системы счета.

Смотрите, как фрекен Снорк использовала ее для записи своих восьмеричных чисел:

• 35₈ = 3 • 8 + 5 = 3 • 8¹ + 5 • 8°.
• 100₈ = 8 • 8 = 8².
• 100₈ = 1 • 8² + 0 • 8¹ + 0 • 8°.
• (Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 36.)

Данный фрагмент текста помогает учащимся выделить в образе таблицы разрядов существенные характеристики, развить известный им образ таблицы разрядов. Школьники имеют возможность осознать, что таблица разрядов для натуральных чисел, записанных в системе счисления, отличной от десятеричной, устроена аналогично, что здесь сохраняется и отражается общий принцип поразрядного значения цифр в записи числа. Методический прием получения текста — варьирование признаков известного образа. Следующие два текста показывают возможности таблицы разрядов для изучения действий над натуральными числами.

Тут в беседу вступил Хемуль.

— Я придумал задачу. Вот она:

«В коллекции одного Хемуля было 2865 натуральных чисел и 3147 десятичных дробей. Сколько всего чисел в коллекции, то есть сколько будет 2865 +.

+ 3147?".

Задачу Хемуля решили в таблице разрядов.

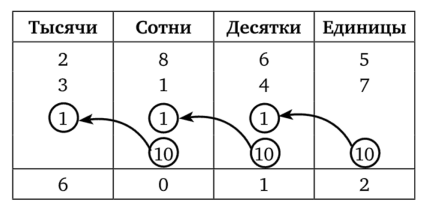
• (Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 79.)
• — А как тебе нравится моя таблица? — спросила фрекен Снорк и показала рисунок.
• — Смотри, как хорошо видно, что при умножении на 10 каждая цифра переходит в левый соседний разряд.
• — Вот теперь я верю! — сказал Снусмумрик.

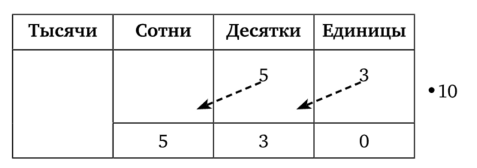
(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 136.).

Подобного рода тексты учат школьников использовать и преобразовывать образ в зависимости от поставленной задачи, то есть развивают такое качество образа, как динамичность.

При изучении действий над десятичными дробями преемственность в использовании образа таблицы разрядов создает условия для формирования целостных знаний учащихся о действиях над натуральными числами и десятичными дробями.

Приведем пример «текста — развитие образа» по разделу «Сложение десятичных дробей».

На помощь пришел Снифф.

— Хороший у тебя пример. Давай, рисуй свою разрядную таблицу. 16,46 кг + 2,845 кг.

Начинаю сложение с меньшего разряда. Так мы поступали и с натуральными числами, — начал комментировать свою таблицу Снусмумрик.

(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 94.).

Следует согласиться с мнением Н. И. Чуприковой, что таблица разрядов может «представлять собой не только систему хранения знаний, но и средство познания» (Чуприкова, 1994, с. 13).

Заметим, что такие тексты особенно важны для учащихся с образным стилем мышления, так как они создают условия для того, чтобы эти школьники активно включались в процесс планирования учебной деятельности, хранили полученные знания в долговременной памяти. Кроме того, они могут оказать помощь школьникам со словесно-речевым стилем мышления, расширяя диапазон их интеллектуального поведения при решении задач.

Среди текстов, развивающих визуальный способ кодирования информации, следует выделить тип текстов, которые можно назвать «текст — мотивация нового образа». Он позволяет привлечь школьников к созданию образа. Учащимся уже известен такой нормативный образ, как числовой луч. В тексте предлагается изучить проблему, решение которой показывает, что известного им образа недостаточно для изображения новых чисел, что нужен новый образ.

Приведем фрагмент учебного текста, в котором возникает необходимость создания нового образа — числовой оси (тема «Положительные и отрицательные числа», 6-й класс).

Буратино. Тюбик, привет! Видал такое: 6−8? Спорим, такую разность нарисовать не сможешь!

Тюбик. Надо попробовать. Некоторые разности я уже изображал на числовом луче. (Рисует.) Начну вот с чего — нарисую разность 6−4. Отмечу точку А, подпишу под ней число 6. От точки, А отсчитаю влево 4 единичных отрезка.

Я попал в точку В, которой соответствует число 2.

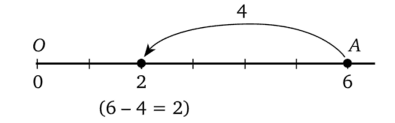
Точно так же я бы мог изобразить разность 6 — 5, 6 — 6. Стоп! А дальше? Как изобразить 6−7 или 6 — 8? Попробую поступить так же.

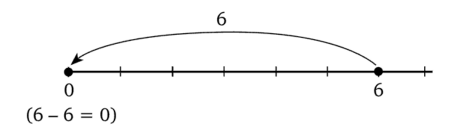
Буратино. Но мне-то нужна разность 6 — 8!

(Математика-5. Ч. 2. Положительные и отрицательные числа, 2005, с. 10.).

Здесь следует сделать паузу и выслушать предложения учащихся, а затем сравнить их с тем, как поступили герои книги.

Мальвина. Не шуми, пожалуйста! У Тюбика идет творческий поиск.

Тюбик. Вот так мне видится разность 6−8.

Буратино. Что это такое?

Мальвина. Тюбику нужно было отсчитать влево от точки Л восемь единичных отрезков. На этом луче столько отрезков не нашлось. Луч кончился. Наш Тюбик вышел из положения — он на этой же прямой нарисовал новый числовой луч с началом в точке О и направленный влево от нее. Теперь Тюбик может свободно двигаться от точки А и влево, и вправо на любое количество единичных отрезков.

(Математика-5. Ч. 2. Положительные и отрицательные числа, 2005, с. 10—11.).

Методический прием, способствующий мотивации нового нормативного образа, — создание ситуации, показывающей, что «старого» образа недостаточно для решения возникшей задачи.

Одним из важнейших качеств нормативных образов является соотнесенность данного образа с рядом других.

Примерами текстов, способствующих развитию данного качества образа, являются тексты, которые можно назвать «текст — классификация образов». В них учащимся предлагается соотнести данный образ с рядом других образов по какому-либо признаку или самим придумать основу классификации.

Развитию умения классифицировать графики функций на основе вполне определенного свойства квадратичной функции способствует, например, такой фрагмент текста (тема «Квадратичная функция», 9-й класс).

На рисунке даны графики квадратичных функций.

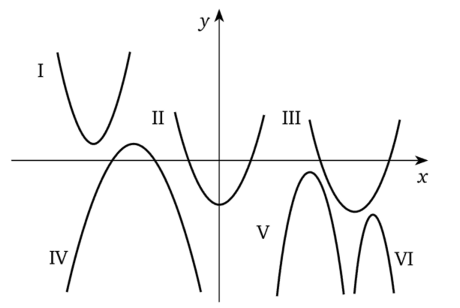
Какой из графиков указывает:

• а) на отсутствие нулей у функции;
• б) на то, что функция имеет только один нуль;
• в) на то, что нули (корни) функции имеют разные знаки;

• г) на то, что оба корня функции положительны;
• д) на то, что оба корня функции отрицательны?
• (Квадратичная функция, 2001, с. 95.)

При подведении итогов изучения графика квадратичной функции предлагается текст, который позволит учащимся обогатить свои знания о способах классификации.

Можно ли сказать, что на рисунке сделана некоторая классификация квадратичных функций (см. рис. ниже)?

Что положено в основу классификации функций? Какую бы классификацию предложили вы?

(Квадратичная функция, 2001, с. 85—86.).

Итак, нами рассмотрены типы текстов, которые способствуют развитию таких свойств нормативных образов, как динамичность, структурированность, обобщенность, системность.

Кодирование информации может осуществляться не только с помощью нормативных образов. Большое значение для умственного развития учащихся имеют индивидуальные образы. К индивидуальным образам мы относим те образы, которые спонтанно возникают у учащихся в процессе изучения того или иного математического понятия и которые связаны с их личным визуальным опытом. Для стимулирования деятельности учащихся по созданию собственных образов, связанных с тем или иным математическим фактом, мы с помощью специальных заданий просим школьников изобразить то, что они представляют себе в связи с изучаемым материалом. Кроме того, мы стараемся с помощью текстов показать возможность зарождения и использования индивидуальных образов.

Такой тип текстов, получивших название «текст — инициация образного опыта», стимулирует учащихся к размышлениям над тем, как можно наглядно представить информацию, настраивает на поиск собственных образных моделей математических объектов.

Так, например, для того чтобы образно зафиксировать идею о возможности записать одно и то же число несколькими способами, учащимся предлагается образ своеобразного мешка, у которого нет дна. Работа с «мешком» начинается в теме «Натуральные числа и десятичные дроби». Приведем фрагмент текстов по теме «Натуральные числа и десятичные дроби» (5-й класс).

Рассмотрите рисунок и скажите, попадут ли в «мешки» следующие числа:

• 20,00; 200,5;
• 1,000; 1,04;
• 1,400; 0,60;

0,006.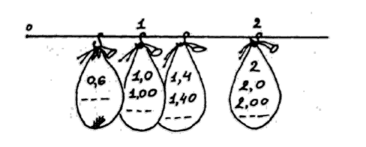

Какие еще числа могут оказаться в этих «мешках»?

Заполните «мешки» соответствующими числами. Как называются числа, соответствующие одной и той же точке на координатном луче?

• 1. Можно ли числа из одного «мешка» переложить в другой?
• 2. Есть ли на рисунке «мешок» для чисел:
• 0,7; 0,070; 0,700; 0,7 000?

Если нет, то нарисуйте такой «мешок».

(Математика-5. Ч. 1. Натуральные числа и десятичные дроби, 2004, с. 219.).

В теме «Рациональные числа» (6-й класс) представление о «мешке» получает развитие и служит визуальной основой при изучении равенства обыкновенных дробей.

Приведем пример еще одного индивидуального образа. Важнейшим этапом в изучении уравнений является развитие умения решать их разными способами. При этом необходима специальная работа, которая позволила бы учащимся осознать такую возможность опознавать уравнения, которые могут быть решены определенным способом. Если использовать образную аналогию, то учащиеся должны уметь «подобрать ключи» к разным уравнениям, которые помогли бы им решать уравнения. Эта идея выражается образно в виде «связки ключей» (тема «Алгебраические дроби», 7-й класс).

(Алгебраические дроби, 2000, с. 174.).

Таким образом, нами рассмотрены типы текстов, которые помогают учащимся кодировать информацию визуально. К ним относятся:

• • текст — формирование нормативного образа;
• • текст — развитие образа;
• • текст — мотивация образа;
• • текст — классификация образов;
• • текст — инициация образного опыта.