Закономерности информетрии и их применение для исследования информационных потоков

Понятие об информетрии

Термин " информетрия"^[1] был введен в начале 80-х гг. XX в. по аналогии с наукометрией, библиометрией для краткой характеристики количественных методов исследования научно-технической информации. Наиболее полно этот термин был раскрыт В. И. Горьковой [6].

Закономерности информетрии определяют распределения информации в документальных информационных потоках (ДИП), количественные и качественные параметры организации частотных словарей, использования слов в текстах документов. ДИП формируют официальные, периодические и продолжающиеся издания и другие опубликованные и неопубликованные документы научно-технической информации. 1

Первые результаты исследований лингвистических закономерностей естественного языка были получены Дж. Эсту (J. В. Estoup, 1916 г.), А. Лоткой (A.J. Lotka, 1926 г.).

Характеристику качественных свойств частотных словарей определил в 1916 г. Дж. Эсту, который обнаружил, что частота использования слов в тексте обратно пропорциональна его номеру в частотном словаре.

Наиболее исследованы закономерности информетрии Г. Ципфа, Б. Мальденброта, С. Брэдфорда, Б. Викери.

Законы Ципфа

George К. Zipf (Дж. Ципф, или в некоторых современных переводах — Г. Зипф) в начале 30-х гг. XX в. на основе статистических исследований получил следующую закономерность^[2].

Допустим, имеется текст длиной N слов и словарь объемом т слов с указанием частоты появления слова в тексте. Слова в словаре расположены в порядке убывания их по частоте и проранжированы от 1 до т. Ранг, равный 1, присваивается слову, частота появления которого наибольшая; ранг, равный т, — наименее употребимому слову. Тогда:

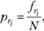
где рri - относительная частота появления слова в тексте; fri — абсолютная частота появления слова ri ранга в тексте определенной длины; N — число слов в тексте; ri — ранг слова, где 1? i? т.

Если умножить вероятность или относительную частоту обнаружения слова в тексте на ранг ri слова, то получим:

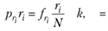
где k — константа; 1? ri ? т.

Если преобразовать формулу, то получим: 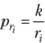, т. е.

функцию типа у = k/x, график которой — равносторонняя гипербола.

Таким образом, на основе анализа полученных зависимостей Ципф предложил эмпирическую формулу, устанавливающую связь между частотой появления слов в тексте и его рангом в словаре:

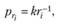
где k — эмпирически определяемая константа, изменяющаяся для разных текстов.

При этом 1? ri ? т; — частота наиболее употребимого слова; рт - частота наименее употребимого слова; рr_i = ср (ri) — «гиперболическая лестница», поскольку ранговое распределение имеет ступенчатый характер (ряд слов появляется с одинаковой частотой), но при аппроксимации можно считать распределение Ципфа гиперболой (рис. 4.9).

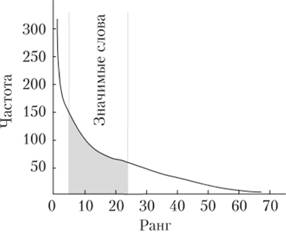
Рис. 4.9. Первый закон Ципфа.

Значение константы в разных языках различно, но внутри одной языковой группы остается неизменно, какой бы текст мы ни взяли. Так, имеются исследования, показывающие, что, например, для английских текстов константа Ципфа равна приблизительно 0,1; а для русского языка — примерно 0,06−0,07.

Поэтому Ципф приводил также запись этого закона в виде.

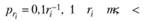
где k = 0,1 (для естественных языков).

Опираясь на экспериментальные данные, собранные в результате статистического исследования многих текстов на различных языках, Ципф обнаружил также, что распределение слов естественного языка подчиняется единому простому закону, который он назвал «принципом наименьшего усилия»: выражая мысли с помощью языка, мы подвергаемся действию двух противоположных сил — силе унификации и силе диверсификации, проявляющихся, с одной стороны, в необходимости быть понятыми, а с другой — желанием выразить мысль покороче.

Ципф установил, что частота и количество слов, входящих в текст с этой частотой, связаны между собой. Если построить зависимость количества слов в данной частоте от частоты вхождения слова, то получится кривая, аналогичная рис. 4.8, которая будет сохранять свои параметры для всех без исключения созданных человеком текстов с некоторыми отклонениями для разных естественных языков (рис. 4.10).

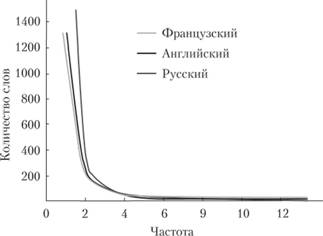
Рис. 4.10. Второй закон Ципфа.

Эту закономерность называют иногда вторым законом Ципфа.

Исследования показали, что наиболее значимые слова лежат в средней части гиперболы (см. рис. 4.9). Слова, которые попадаются слишком часто, в основном оказываются предлогами, местоимениями, в английском — артиклями и т. п. Редко встречающиеся слова тоже в большинстве случаев не имеют решающего смыслового значения.

От того как будет выставлен диапазон значимых слов, зависят свойства информационно-поисковой системы.

Если применить более широкий диапазон, нужные термины потонут в море вспомогательных слов; если установить узкий диапазон — можно потерять смысловые термины. В каждой поисковой системе эта проблема решается по-своему, с учетом общего объема текста, специальных словарей и т. п.

Таким образом, законы Ципфа отражают некоторое общее свойство, присущее разным языкам. Это свойство заключается в том, что в каждом тексте на любом естественном языке имеется некоторое количество наиболее употребимых слов. Причем число этих слов значительно меньше общего числа слов, используемых в тексте.

Законы Ципфа универсальны. В принципе, они применимы не только к текстам.

В аналогичную форму выливается, например, зависимость количества городов от числа проживающих в них жителей. Характеристики популярности узлов в сети Интернет — тоже отвечают законам Ципфа.

Законы Ципфа проявляются и при исследовании документальных информационных потоков (ДИП). В этом случае первый закон Ципфа представляют через абсолютную частоту появления слов:

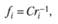
где fi — абсолютная частота появления слова в текстах документального потока; ri - ранг слова в ранговом распределении; С — частота появления слова 1-го ранга, которую для данного ДИП можно считать эмпирической константой.

• [1] Bonitz М. Scientometrie, Bibliometrie, Informetrie / М. Bonitz // Zbl. Biblioteksw. 1982. Vol. 86. № 1. S. 19−24.
• [2] Zipf G. К. Human behaviory and principle of ieast effort / G. K. Zipf // Cambridge (Mass.): Addisson — Wesiey, 1949. Vol. XI; Zipf G. K. Selected studies of the principle of relative frequency in language / G. K. Zipf // Cambridge (Mass.): Harvard Univ. Press., 1932.