Геометрический смысл решений неравенств, уравнений и их систем

Каждое из неравенств в соответствии с теоремой 2.3 определяет одну из полуплоскостей, являющуюся выпуклым множеством точек. Множеством решений совместной системы линейных неравенств служат точки, которые принадлежат полуплоскостям решений всех неравенств, т. е. принадлежат их пересечению. Согласно теореме 2.2 о пересечении выпуклых множеств это множество является выпуклым и содержит конечное… Читать ещё >
Геометрический смысл решений неравенств, уравнений и их систем (реферат, курсовая, диплом, контрольная)
Рассмотрим решения неравенств.
Теорема 2.3. Множество решений неравенства с двумя переменными
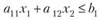 (2.2).
(2.2).
является одной из двух полуплоскостей, па которые вся плоскость делится прямой аЛ[х{ +а l2x2 =bv включая и эту прямую, а другая полуплоскость с той же прямой есть множество решений неравенства
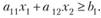 (2.3).
(2.3).
? Для произвольной абсциссы х, ордината точки М (рис. 2.6), лежащей на прямой 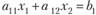 , при условии
, при условии 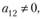 есть
есть 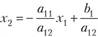 •, т. е. координаты точки
•, т. е. координаты точки 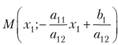
Через точку М проведем прямую, параллельную оси Ох2. Тогда для любых точек Р и Q этой прямой, расположенных выше и ниже точки М, т. е. в верхней и нижней полуплоскостях, будут верны неравенства 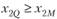 и
и  или
или 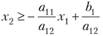 и
и 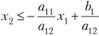 . При условии
. При условии 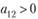 неравенства преобразуются соответственно к виду
неравенства преобразуются соответственно к виду  и
и 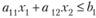 , т. е. координаты.
, т. е. координаты.
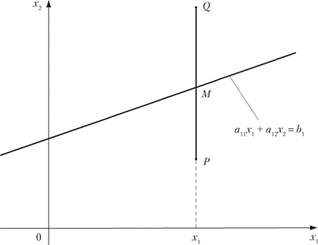
Рис. 2.6.
всех точек верхней полуплоскости удовлетворяют неравенству (2.2), а нижней полуплоскости — неравенству (2.3). В случае а12 <0, наоборот, координаты всех точек верхней полуплоскости удовлетворяют неравенству (2.3), а координаты нижней полуплоскости — неравенству (2.2). ¦
2.4. Построить множество решений неравенства:

Решение. В соответствии с теоремой 2.3 множество решений неравенства есть полуплоскость.
1) Построим границу полуплоскости — прямую З. г, -4×2 + 12 = 0, найдя точки ее пересечения с осями координат А (-4;0) и В (0;3) на рис 2.7, а.
Для определения искомой полуплоскости (верхней или нижней) рекомендуется задать произвольную контрольную точку, не лежащую на ее границе — построенной прямой. Если неравенство выполняется в контрольной точке, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку, и не выполняется во всех точках другой полуплоскости. И наоборот, в случае невыполнения неравенства в контрольной точке оно не выполняется во всех точках полуплоскости, содержащей контрольную точку, и выполняется во всех точках другой полуплоскости.
В качестве контрольной точки удобно взять начало координат О (0;0), не лежащее на построенной прямой. Координаты точки О не удовлетворяют неравенству: 3 • 0 — 4 • 0 +12 < 0, следовательно, решением данного неравенства является верх;
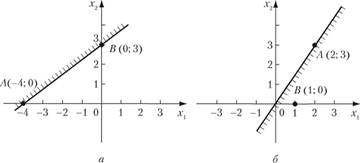
Рис. 2.7.
няя полуплоскость, не содержащая контрольную точку О. Искомая полуплоскость выделена штриховкой.
2) Построим границу полуплоскости — прямую З. г, — Ах2 = 0 по двум точкам. Одной из этих точек является начало координат на рис. 2.7, б (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например А (2;3) на рис. 2.7, б. В качестве контрольной возьмем, например, точку В (1;0). Самую «простую» точку О (0;0) здесь в качестве контрольной брать не следует, поскольку она лежит на построенной прямой. Так как координаты контрольной точки В (1; 0) удовлетворяют неравенству, т. е. 3 • 1 — 2 • 0 > 0, то решением данного неравенства является нижняя (правая) полуплоскость, содержащая эту точку. >
Учитывая, что множество точек, удовлетворяющих уравнению.
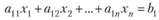 (2.4).
(2.4).
при п = 3, является плоскостью, а при п > 3 ее обобщением в n-мерном пространстве — гиперплоскостью, теорему 2.3 можно распространить на случай трех и более переменных.
Теорема 2.4. Множество всех решений линейного неравенства с п переменными является одним из полупространств, на которые все пространство делится плоскостью или гиперплоскостью (2.4), включая и эту плоскость (гиперплоскость).
Рассмотрим множество решений систем неравенств.
Теорема 2.5. Множество решений совместной системы т линейных неравенств с двумя переменными
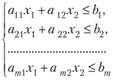
является выпуклым многоугольником (или выпуклой многоугольной областью).
Каждое из неравенств в соответствии с теоремой 2.3 определяет одну из полуплоскостей, являющуюся выпуклым множеством точек. Множеством решений совместной системы линейных неравенств служат точки, которые принадлежат полуплоскостям решений всех неравенств, т. е. принадлежат их пересечению. Согласно теореме 2.2 о пересечении выпуклых множеств это множество является выпуклым и содержит конечное число угловых точек, т. е. является выпуклым многоугольником (выпуклой многоугольной областью). ¦
2.5. Построить множество решений системы неравенств.
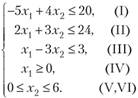
Решение. Для построения искомого множества решений системы неравенств находим последовательно множество решений каждого неравенства аналогично тому, как это делалось в задаче 2.4. Рекомендуем после определения каждой полуплоскости и выделения ее соответствующей штриховкой находить последовательно их пересечение: сначала полуплоскостей решений первых двух неравенств (многоугольной области GFD на рис. 2.8), затем первых трех неравенств (треугольника GFD), потом — четырех неравенств (четырехугольника HAFD), далее — пяти неравенств (пятиугольника OAFDE) и, наконец, всех шести неравенств — выпуклого многоугольника OABCDE.
Координаты угловых точек — вершин этого многоугольника — найдем как координаты точек пересечения соответствующих прямых. Например, точка D является точкой пересечения прямых II и III, т. е. ее координаты являются решением системы.
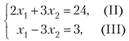
откуда .г, =9, х2 = 2, т. е. D (9; 2). Аналогично находим координаты других угловых точек: О (0; 0), А (0; 5), В (4/5; 6), С (3; 6), Е (3;0). >
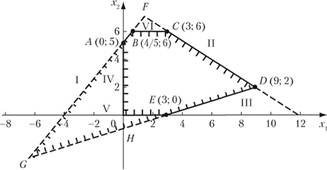
Рис. 2.8.
При построении областей решений систем неравенств могут встретиться и другие случаи: множество решений — выпуклая многоугольная область (рис. 2.9, а); одна точка (рис. 2.9, б); пустое множество, когда система неравенств несовместна (рис. 2.9, в).
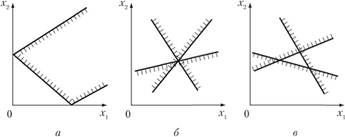
Рис. 2.9.
Теорема 2.6. Множество решений совместной системы т линейных неравенств с п переменными является выпуклым многогранником (выпуклой многогранной областью) в п-мерном пространстве.
Рассмотрим множество допустимых решений системы т линейных уравнений с п переменными.
Теорема 2.7. Множество всех допустимых решений совместной системы т линейных уравнений с п переменными (т < п) является выпуклым многогранником (выпуклой многогранной областью) в п-мерном пространстве.
Доказательство этой теоремы приведено в гл. 3. Здесь же проиллюстрируем теорему на примерах.
- 2.6. Построить множество допустимых решений:
- а) уравнения
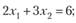
- б) системы уравнений
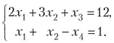
- а) уравнения
Убедиться в справедливости теоремы 2.7.
Решение. 1) Рассмотрим частный случай системы линейных уравнений (т < п), содержащей п = 2 переменных, т. е. состоящей из одного уравнения (т = 1). Множество всех решений данного уравнения есть прямая 2хх + Зх2 = 6, а множество допустимых решений (при дополнительном условии хх >0, х2 > 0) — точки отрезка АВ (рис. 2.10, а), который можно рассматривать как частный случай выпуклого многогранника с двумя угловыми точками А (3;0) и В (0;2).
2) Построить непосредственно множество решений системы уравнений с п = 4 (п > 3) переменными не представляется возможным. В данном случае (когда разность между числом переменных и уравнений п — т = 2) можно поступить так: разобьем все переменные на основные, например хъ и xi (определитель из коэффициентов при них, или базисный минор, отличен от нуля), и неосновные (свободные) переменные зг, и х., и вместо множества решений системы построим множество значений их неосновных переменных (выполнить это возможно, так как их всего две).
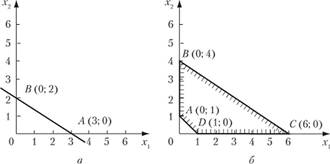
Рис. 2.10.
С этой целью выразим основные переменные через неосновные:
Так как рассматриваются допустимые значения переменных, т. е. х{ >0, х2 > 0, х3 > 0, х4 > 0, то Решениями полученной таким образом системы неравенств являются точки четырехугольника ABCD на рис. 2.10, 6 с четырьмя угловыми точками А (0; 1), В (0;4), С (6; 0), D (1;0) (рекомендуем убедиться в этом самому читателю).
В данном примере графические построения проведены не в пространстве всех переменных, а в плоскости двух неосновных переменных х, хт, Но так как любой паре неосновных переменных х{, х2 соответствуют определенные значения основных переменных х3, х4, а следовательно, одно и только одно решение данной системы уравнений, то каждой точке построенного четырехугольника ABCD соответствует одна и только одна точка множества допустимых решений системы уравнений, представляющего в данном случае выпуклый многогранник в четырехмерном пространстве. >
Между допустимыми базисными решениями и угловыми точками множества допустимых решений системы линейных уравнений существует взаимно-однозначное соответствие. Это утверждение будет доказано в гл. 3, здесь же ограничимся примером.
2.7. Убедиться в том, что между базисными решениями систем, приведенных в задаче 2.6, и угловыми точками множества их допустимых решений существует взаимно-однозначное соответствие.
Решение. 1) Система, состоящая из одного уравнения, имеет два допустимых базисных решения. Первое базисное решение = (3; 0) получается из уравнения, если в качестве основной взять переменную xv, а неосновной — переменную х2 = 0. Второе базисное решение Х2 = (0; 2) получается, если основная переменная х2, а неосновная переменная х4 = 0. Из рис. 2.10, а следует, что допустимым базисным решениям.
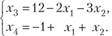
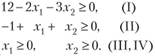
X, и Х2 однозначно соответствуют угловые точки отрезка А В — множества допустимых решений уравнения.
2) Для системы, приведенной в задаче 2.6, б, можно получить четыре допустимых базисных решения (рекомендуем читателю найти их самостоятельно): X, = (1; 0; 10; 0), Х2 = (6; 0; 0; 5), X, = (0; 1; 9; 0), Х4 = (0; 4; 0; 3). Из рис. 2.10, б следует, что этим допустимым базисным решениям однозначно соответствуют точки D (1; 0), С (6; 0), А (0; 1) и В (0;4) многоугольника ABCD — множества допустимых решений системы уравнений. >