Электромагнитное поле в проводниках с линейными свойствами

Электрический поверхностный эффект в проводнике с линейными свойствами

Экспериментально установлено и теоретически подтверждено, что переменный электрический ток неравномерно распределяется по сечению проводника. При этом плотность тока возрастает по мере перемещения из глубины проводника к его поверхности. Это явление называют электрическим поверхностным эффектом.

На рис. 2.1 изображен проводник прямоугольного сечения 2axb, обтекаемый током /. Поле в проводнике удовлетворяет уравнению Гельмгольца:

Внутри проводника существуют электромагнитное поле и ток проводимости. За пределами проводника ток проводимости отсутствует, но электрическое и магнитное поля существуют. Поскольку внутреннее и внешнее электромагнитные поля взаимосвязаны, то при решении задачи о расчете поля внутри проводника необходимо знать законы распределения поля и за его пределами.

Таким образом, при строгом подходе нужно решать задачу о распределении поля во всем пространстве — внутри и за пределами проводника.

Поскольку эта задача очень сложна для точного аналитического решения, сформулируем такие условия и допущения, при которых задачу о поверхностном эффекте в проводнике можно будет решить приближенно с хорошей точностью.

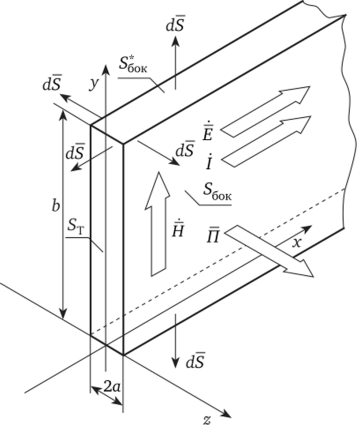
Рис. 2.7.

Исходя из методологических соображений, рассмотрим вначале поле в проводнике круглого сечения (рис. 2.2, а). Магнитные линии представляют собой концентрические окружности. Магнитный поток, обусловленный током в проводнике, разделяется на две составляющие — внутренний и внешний. Это свойство проводника круглого сечения используется в инженерной практике при определении его внутренней индуктивности.

При квадратном сечении проводника (рис. 2.2, б) такого четкого разделения потоков сделать нельзя, так как контур сечения уже не является силовой линией.

Но по мере увеличения соотношения — (рис. 2.2, в) сило;

2 а

вые линии внутри проводника начинают принимать очертания, приближающиеся к форме его внешнего контура. И при.

— «1 практически во всем объеме проводника вектор магнитной напряженности становится направленным вдоль большей боковой поверхности проводника.

Если теперь пренебречь краевыми эффектами, то при — «1.

2 а

возможно решение одномерной задачи в предположении, что электрическая и магнитная напряженности являются функциями координаты z:

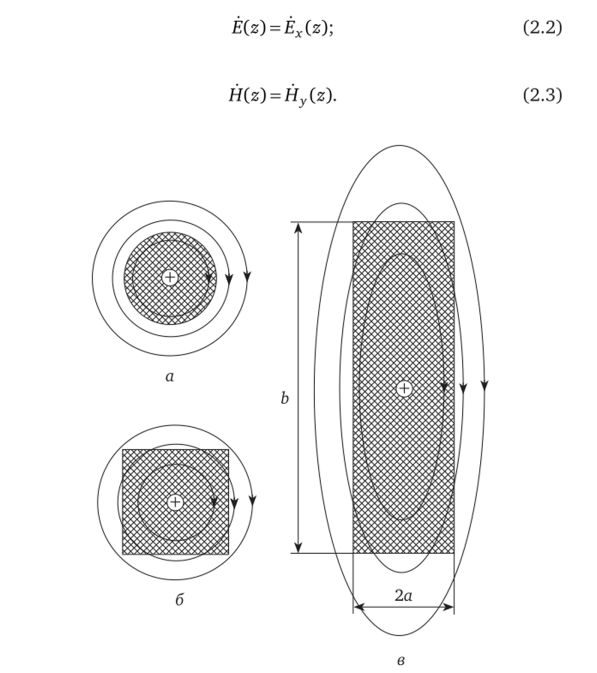
Рис. 2.2.

Поставим задачу рассчитать распределение поля Е и Н в объеме проводника прямоугольного сечения (см. рис. 2.1) и вычислить его комплексное сопротивление синусоидальному току, если проводник с — «1 обтекается током I с частотой со.

Параметры среды — ц и у — постоянны. При принятом допущении об одномерности поля уравнение Гельмгольца (2.1) принимает вид.

Решением уравнения (2.4) является совокупность экспоненциальных функций:

Общее решение для магнитной напряженности в соответствии со вторым уравнением Максвелла:

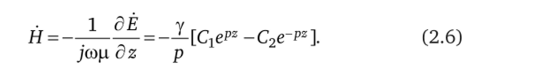
Поскольку поле Ё обладает четной симметрией, а поле Н — нечетной симметрией относительно оси оу, линейные комбинации экспонент в (2.5) и (2.6) можно представить в виде гиперболических функций:

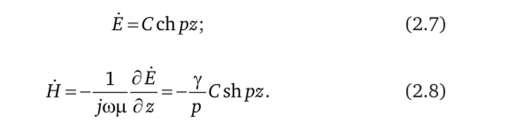
Постоянная интегрирования в (2.7) и (2.8) пропорциональна току в проводнике I. Ток в проводнике связан с плотностью тока соотношением:

Поскольку §(z) = y?(z), a dS = bdz, выражение (2.9) принимает вид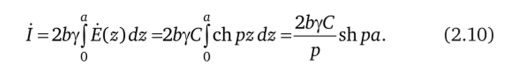

В итоге решения (2.7) и (2.8) принимают вид.

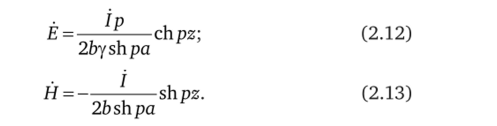
Интерес представляет качественный анализ плотности тока в объеме проводника (рис. 2.3).

В соответствии с законом Ома 8 = у? из (2.12) имеем:

Картина распределения 8(z), очевидно, будет зависеть от коэффициента распространения р. На низких частотах параметр — мал, и ра «1. При малом аргументе chpz «1; shpa яра, A.

и тогда (2.14) имеет вид.

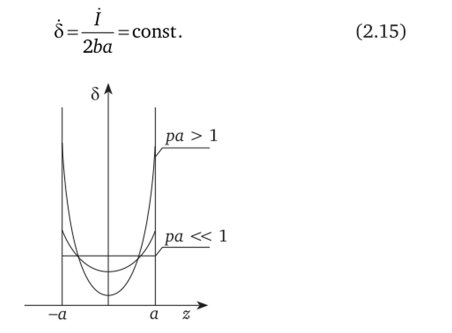
Рис. 2.3.

Как видно из (2.15), на низких частотах ток равномерно распределяется по сечению проводника, а поверхностный эффект не проявляется.

По мере роста частоты картина изменяется, поскольку с ростом параметра ра увеличивается неравномерность распределения тока по сечению проводника.

Из графика на рис. 2.4 видно, что при переходе через начало координат функция H (z) меняет знак. Кроме того, на поверхности проводника Н (а) =—, что соответствует закону пол;

• 2 Ъ
• 1 z

ного тока. При ра"1 Н =—, т. е. при слабо выраженном.

2 Ьа

поверхностном эффекте функция H (z) изменяется по линейному закону. С ростом параметра ра поверхностный эффект начинает проявляться.

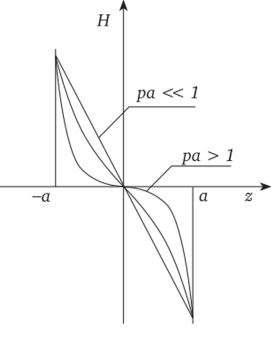
Рис. 2.4.

Воспользуемся выражением (1.128) для вычисления комплексного сопротивления проводника. Рассмотрим кусок проводника длиной I (см. рис. 2.1). Будем полагать, что замкнутая поверхность, его охватывающая, состоит из следующих частей:^замкн — 2S_6oK + 2S6_0K + 2S_T. _.

Поскольку на поверхностях S_T и Sq_ok векторы П и dS взаимно перпендикулярны, потоки энергии поступают в проводник только через боковые вертикальные поверхности, и в силу осевой симметрии задачи эти потоки одинаковы. Это означает, что.

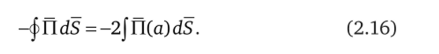
Поскольку в любой плоскости, параллельной хоу, П = const, то интеграл в правой части (2.16) обратится в произведение n (a)S_6oK, а (2.16) примет вид.

Подставив (2.12) и (2.13) в (2.17) с учетом того, что.

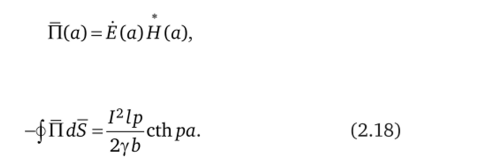
получим Поделив (2.18) на квадрат тока, найдем комплексное сопротивление проводника, имеющего длину I:

Заметим, что при выводе выражения для комплексного сопротивления (2.19) учитывалась не вся энергия магнитного поля, создаваемая проводником, а только та ее часть, что заключена внутри объема проводника. Поэтому комплексное сопротивление, вычисленное по (2.19), называется внутренним сопротивлением. ^.

На низких частотах ра «1. При малом аргументе cth ра «—, и (2.19) принимает вид Р^а

а сопротивление становится равным сопротивлению проводника постоянному току.

На высоких частотах уже при ра> 2 и cth ра «1, и (2.19) принимает вид:

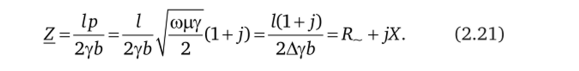
Из (2.21) следует, что при ярко выраженном поверхностном эффекте активное сопротивление проводника синусоидальному току становится равным.

Таким образом, эффективное сечение проводника определяется удвоенным значением глубины проникновения.

Введем в рассмотрение коэффициенты поверхностного эффекта^[1] как отношение сопротивлений проводника переменному току к его активному сопротивлению постоянному току:

Поскольку для проводника прямоугольного сечения.

=-, при подстановке (2.19) в (2.23) и (2.24) получим:

2aby

Представляют интерес зависимости коэффициентов к_г и к_х

ГГ

от параметра I——, где Я₁₀₀ — сопротивление постоянному Uwo

току проводника длиной 100 м.

На рис. 2.5—2.7 представлены подобные кривые, рассчитанные для медного и алюминиевого проводника на частотах в диапазоне 50—10 000 Гц. Геометрический параметр а изме;

няется в пределах 0,5—200 мм; отношение — равно 20.

а

Вне зависимости от удельного сопротивления и геометрических размеров проводников все рассчитанные точки ложатся на одну гладкую кривую.

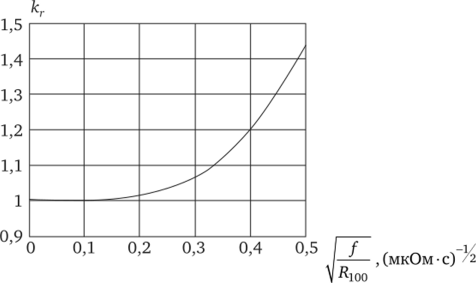
Рис. 2.5.

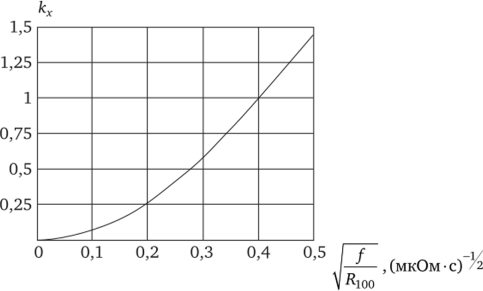
Рис. 2.6.

При малых значениях параметра 1—^— кривая к_г стремится.

V^юо к единице (см. рис. 2.5), кривая к_х — к нулю (рис 2.6). При возрастании параметра I—графики к_г и к_х сливаются, предV ^100.

ставляя собой линейную функцию (рис. 2.7).

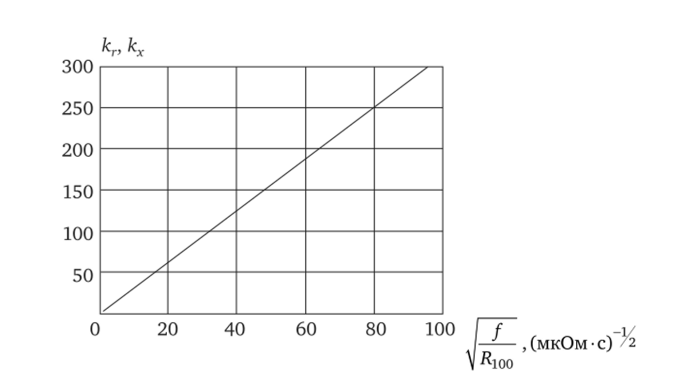
Рис. 2.7.

• [1] Установки индукционного нагрева: учеб, пособие для вузов / А. Е. Слу-хоцкий [и др.]; под ред. А. Е. Слухоцкого. М.: Энергоиздат, 1981.