Синтез алгоритма управления в задаче слежения

Управление (6.26) легко можно распространить на задачу слежения, включив в него величину, определяющую желаемое движение.

Пусть 2/_ж(?) определяет желаемую траекторию. Для ошибки слежения и ее производных по времени введем обозначения.

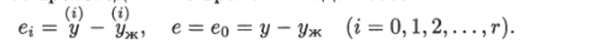aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">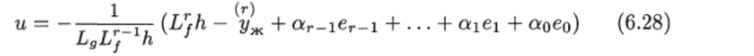

При законе управления уравнение замкнутой системы примет вид.

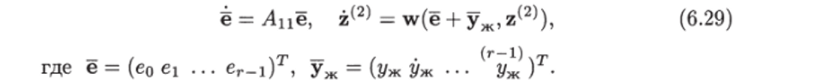
Теорема 6.5. Пусть система (6.18) имеет относительную степень г < п и нуль-динамика экспоненциально устойчива.

Тогда если полином (6.25) устойчив и желаемая траектория у_ж(1) ^ ее г — 1 производных достаточно малы, то управление (6.28) обеспечивает сходимость к нулю ошибки слежения при неограниченном увеличении времени и ограниченность переменных внутренней динамики: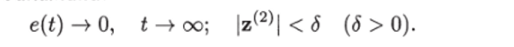

Доказательство. Так как внешняя динамика системы (6.29), представляющая устойчивую линейную систему, экспоненциально устойчива, то ошибка слежения e (t) сходится к нулю экспоненциально. Поэтому достаточно показать, что внутреннее состояние z⁽²⁾ остается ограниченным, когда e (t) -> 0 при t —? 00.

Для этого воспользуемся прямым методом Ляпунова. Но прежде всего отметим следующее.

• а) Так как по условию у_ж(*) и ее г — 1 производных достаточно малы (ограничены), то существует положительное число 5i такое, что у_ж < 6.
• б) Так как w (z^, z^) — гладкая функция, то выполняется условие Липшица

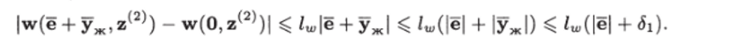
в) Так как нуль-динамика экспоненциально устойчива, то согласно теореме Красовского (см. гл. 7) для нее существуют функция Ляпунова где Р — положительно определенная матрица, удовлетворяющая уравнению Ляпунова

/i — положительная постоянная. Как было установлено выше, матрица Ап является устойчивой. Поэтому положительно определенная матрица Р, удовлетворяющая уравнению Ляпунова, существует. Производная искомой функции Ляпунова по времени в силу уравнения (6.29) имеет вид.

и положительные числа ci, С2, сз, с* такие, что справедливы неравенства.

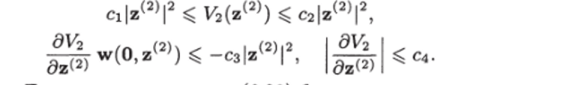
Функцию Ляпунова для системы (6.29) будем искать в виде.

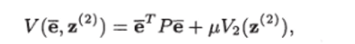
Исключив два отрицательных слагаемых (третье и четвертое), последнее неравенство можно представить в виде.

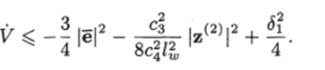
Отсюда следует, что производная V < 0, когда |ё| и |z⁽²⁾| принимают большие значения. Следовательно, переменные внутреннего состояния ограничены.

В общем случае устойчивость нуль-динамики гарантирует только локальную устойчивость (устойчивость в малом) системы управления, синтезированной на основе линеаризации обратной связью по выходу.

Задачи

• 1. Вычислить производные Ли 1-го и 2-го порядков функции h (x) по векторной функции f (x), если h (x) и f (x) имеют следующий вид:
  • а) /i (x) = х + х, f (x) = (Х2 х + хъ)^т
  • б) /i (x) = xj + хХ2 + х, f (x) = (x2 + Xi х — х^)⁷;
  • в) h (x) = х + х + х, f (x) = (х₂ хз Xi-2x2-xl)^T.
• 2. Вычислить скобки Ли 1-го и 2-го порядков функций g (x) и f (x), имеющих следующий вид:
  • а) g (x) = (О 1)^т, f (x) = (х Xi)^T
  • б) g (x) = (О 2)^т, f (x) = (х х)^т
  • в) g (x) = (1 0)^т, f (x) = (х₂ А)^Т

^г) g (^x) = (0 0 l)^r, f (x) = {х₂ + е~^Х2х₃ х₃ 0)^т.

3. Показать линеаризуемость обратной связью по состоянию и определить соответствующие линеаризующие преобразования следующих систем:

a) xi = Х2, Х2 = х + и б) xi = Х2, &2 = х + 2и;

• в) Xi = Х2, Х2 = Х1Х2 + 2u; г) Xi = Х2, Х2 = Xi + u;
• д) xi = Х2 + u, Х2 = я?; е) xi = Х2 + и, Х2 = хх₂-
• 4. Показать, что система

Х = Х2 + е" «^Х2хз, Х2 = хз, хз = и линеаризуема обратной связью по состоянию.

5. Показать, что система

Xi = Х2 + е"^хзХ2, Х2 — хз, Хз = и не линеаризуема обратной связью по состоянию.