Упражнения. 
Теория вероятностей

• 3.25. Вероятность поражения вирусным заболеванием куста земляники равна 0,2. Составить закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных кустов.
• 3.26. Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,2. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составить закон распределения числа очков, полученных стрелком за 3 выстрела, и вычислить математическое ожидание этой случайной величины.
• 3.27. В рекламных целях торговая фирма вкладывает в каждую десятую единицу товара денежный приз размером 1 тыс. руб. Составить закон распределения случайной величины — размера выигрыша при пяти сделанных покупках. Найти математическое ожидание и дисперсию этой случайной величины.
• 3.28. Клиенты байка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения числа возвращенных в срок кредитов из 5 выданных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
• 3.29. Контрольная работа состоит из трех вопросов. На каждый вопрос приведено 4 ответа, один из которых правильный. Составить закон распределения числа правильных ответов при простом угадывании. Найти математическое ожидание и дисперсию этой случайной величины.
• 3.30. В среднем по 10% договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Составить закон распределения числа таких договоров среди наудачу выбранных четырех. Вычислить математическое ожидание и дисперсию этой случайной величины.
• 3.31. В билете три задачи. Вероятность правильного решения первой задачи равна 0,9, второй — 0,8, третьей — 0,7. Составить закон распределения числа правильно решенных задач в билете и вычислить математическое ожидание и дисперсию этой случайной величины.
• 3.32. Вероятность попадания в цель при одном выстреле равна 0,8 и уменьшается с каждым выстрелом на 0,1. Составить закон распределения числа попаданий в цель, если сделано три выстрела. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
• 3.33. Произведено два выстрела в мишень. Вероятность попадания в мишень первым стрелком равна 0,8, вторым — 0,7. Составить закон распределения числа попаданий в мишень. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины и построить ее график. (Каждый стрелок делает по одному выстрелу.)
• 3.34. Найти закон распределения числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5, 0,6, 0,7. Найти математическое ожидание и дисперсию данной случайной величины, построить функцию распределения.
• 3.35. Дан ряд распределения случайной величины

Найти функцию распределения этой случайной величины, если ее математическое ожидание равно 3,4, а дисперсия равна 0,84.

• 3.36. Из пяти гвоздик две белые. Составить закон распределения и найти функцию распределения случайной величины, выражающей число белых гвоздик среди двух одновременно взятых.
• 3.37. Из 10 телевизоров на выставке 4 оказались фирмы «Сони». Наудачу для осмотра выбрано 3. Составить закон распределения числа телевизоров фирмы «Сони» среди 3 отобранных.
• 3.38. Среди 15 собранных агрегатов 6 нуждаются в дополнительной смазке. Составить закон распределения числа агрегатов, нуждающихся в дополнительной смазке, среди пяти наудачу отобранных из общего числа.
• 3.39. В магазине продаются 5 отечественных и 3 импортных телевизора. Составить закон распределения случайной величины — числа импортных из четырех наудачу выбранных телевизоров. Найти функцию распределения этой случайной величины и построить ее график.
• 3.40. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые посетит студент, если в городе 4 библиотеки. Найти математическое ожидание и дисперсию этой случайной величины.
• 3.41. Экзаменатор задает студенту вопросы, пока тот правильно отвечает. Как только число правильных ответов достигнет четырех либо студент ответит неправильно, экзаменатор прекращает задавать вопросы. Вероятность правильного ответа на один вопрос равна 2/3. Составить закон распределения числа заданных студенту вопросов.
• 3.42. Торговый агент имеет 5 телефонных номеров потенциальных покупателей и звонит им до тех пор, пока не получит заказ на покупку товара. Вероятность того, что потенциальный покупатель сделает заказ, равна 0,4. Составить закон распределения числа телефонных разговоров, которые предстоит провести агенту. Найти математическое ожидание и дисперсию этой случайной величины.

• 3.43. Каждый поступающий в институт должен сдать 3 экзамена. Вероятность успешной сдачи первого экзамена равна 0,9, второго — 0,8, третьего — 0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения числа экзаменов, сдававшихся поступающим в институт. Найти математическое ожидание этой случайной величины.
• 3.44. Охотник, имеющий 4 патрона, стреляет по дичи до первого попадания или до израсходования всех патронов. Вероятность попадания при первом выстреле равна 0,6, при каждом последующем — уменьшается на 0,1. Необходимо: а) составить закон распределения числа патронов, израсходованных охотником; б) найти математическое ожидание и дисперсию этой случайной величины.
• 3.45. Из поступивших в ремонт 10 часов 7 нуждаются в общей чистке механизма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в чистке, рассматривает их поочередно и, найдя такие часы, прекращает дальнейший просмотр. Составить закон распределения числа просмотренных часов. Найти математическое ожидание и дисперсию этой случайной величины.
• 3.46. Имеются 4 ключа, из которых только один подходит к замку. Составить закон распределения числа попыток открывания замка, если испробованный ключ в последующих попытках не участвует. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
• 3.47. Абонент забыл последнюю цифру нужного ему номера телефона, однако помнит, что она нечетная. Составить закон распределения числа сделанных им наборов номера телефона до попадания на нужный номер, если последнюю цифру он набирает наудачу, а набранную цифру в дальнейшем не набирает. Найти математическое ожидание и функцию распределения этой случайной величины.
• 3.48. Дана функция распределения случайной величины X

Найти: а) ряд распределения; б) М (Х) иО (АГ); в) построить многоугольник распределения и график г).

3.49. Даны законы распределения двух независимых случайных величин.

Найти вероятности, с которыми случайные величины принимают значение 3, а затем составить закон распределения случайной величины ЗХ -2 У и проверить выполнение свойств математических ожиданий и дисперсий: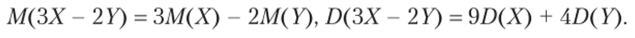

3.50. На двух автоматических станках производятся одинаковые изделия. Даны законы распределения числа бракованных изделий, производимых в течение смены на каждом из них:

Необходимо: а) составить закон распределения числа производимых в течение смены бракованных изделий обоими станками; б) проверить свойство математического ожидания суммы случайных величин.

3.51. Одна из случайных величин задана законом распределения.

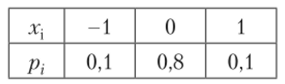
а другая имеет биномиальное распределение с параметрами п = 2, р = 0,6. Составить закон распределения их суммы и найти математическое ожидание этой случайной величины.

3.52. Случайные величины X и У независимы и имеют один и тот же закон распределения:

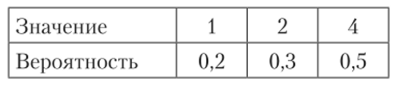
Составить закон распределения случайных величин 2Х и X + У. Убедиться в том, что 2Х Ф X + У, но М (2Х) = М (Х + У).

• 3.53. По данным примера 3.52 убедиться в том, что X² * ХУ. Проверить равенство М (ХУ) = [М (Х)².
• 3.54. Два стрелка сделали по два выстрела, но мишени. Вероятность попадания в мишень для первого стрелка равна 0,6, для второго — 0,7. Необходимо: а) составить закон распределения общего числа попаданий; б) найти математическое ожидание и дисперсию этой случайной величины.
• 3.55. Пусть X, У, X — случайные величины: X — выручка фирмы, У — ее затраты, X — X — У — прибыль. Найти распределение прибыли X, если затраты и выручка независимы и заданы распределениями:

3.56. Пусть X — выручка фирмы в долларах. Найти распределение выручки в рублях X — X • У в пересчете по курсу доллара У, если выручка X не зависит от курса У, а распределения X и У имеют вид.

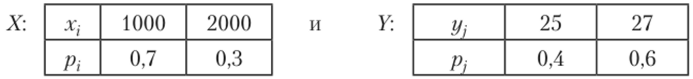
• 3.57. Сделано два высокорисковых вклада: 10 тыс. руб. — в компанию Л и 15 тыс. руб. — в компанию В. Компания Л обещает 50% годовых, но может «лопнуть» с вероятностью 0,2. Компания В обещает 40% годовых, но может «лопнуть» с вероятностью 0,15. Составить закон распределения случайной величины — общей суммы прибыли (убытка), полученной от двух компаний через год, и найти ее математическое ожидание.
• 3.58. Дискретная случайная величина X задана рядом распределения

Найти условную вероятность события X < 5 при условии, что X > 2.

3.59. Случайные величины Х_1? Х₂ независимы и имеют одинаковое распределение.

Найти: а) вероятность события Х_х + Х₂ > 2; б) условную вероятность P_Xl=1[(X₁₊X₂)>2].

3.60. Распределение дискретной случайной величины X задано формулой р (Х = k) = Ck²_y где k = 1, 2, 3, 4, 5.

Найти: а) константу С; б) вероятность события Х — 2| < 1.

3.61. Распределение дискретной случайной величины X определяется формулой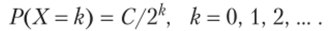

Найти: а) константу С; б) вероятность Р (Х <3).

3.62. Случайная величина X, сосредоточенная на интервале [-1; 3],.

задана функцией распределения 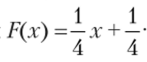Найти вероятность попадания случайной величины X в интервал [0; 2]. Построить график функции ад.

3.63. Случайная величина X, сосредоточенная на интервале [2; 6], задана функцией распределения 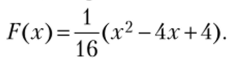Найти вероятность того, что случайная величина X примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.

3.64. Случайная величина X, сосредоточенная на интервале (1; 4), задана квадратичной функцией распределения F (x) = ах² + Ьх + с, имеющей максимум при х = 4. Найти параметры а_уЬ>с и вычислить вероятность попадания случайной величины X в интервал [2; 3].

3.65. Дана функция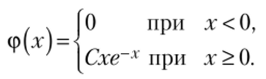

При каком значении параметра С эта функция является плотностью распределения некоторой непрерывной случайной величины X? Найти математическое ожидание и дисперсию случайной величины X.

3.66. Случайная величина X задана функцией распределения.

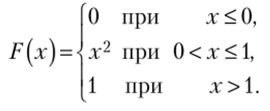
Найти: а) плотность вероятности ф (х); 6) математическое ожидание М (Х); в) дисперсию D (X); г) вероятности Р (Х = 0,5), Р (Х < 0,5), Р (0,5 < X < 1); д) построить рафики ср (х) и F (x) и показать на них математическое ожидание М (Х) и вероятности, найденные в п. г).

3.67. По данным примера 3.66 найти: а) моду и медиану случайной величины X; б) квантиль х_{0 4} и 20%-ную точку распределения X.

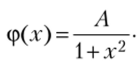
• 3.68. По данным примера 3.66 найти коэффициент асимметрии и эксцесс случайной величины X.
• 3.69. Случайная величина X распределена по закону Коши:

Найти: а) коэффициент А; 6) функцию распределения F (x); в) вероятность.

Р(-1 <�Х < 1). Существуют ли для случайной величины X математическое ожидание и дисперсия?

• 3.70. Случайная величина X распределена, но закону Лапласа: ф (д*) = = Ае~^к™. Найти: а) коэффициент А; б) функцию распределения F (x); в) математическое ожидание М (Х) и дисперсию D (X). Построить графики ф (х) и F (x).
• 3.71. Случайная величина X распределена по закону «прямоугольного треугольника» в интервале (0; с) (рис. 3.21). Найти: а) выражение плотности вероятности ф (_г) и функции распределения F (x); б) математическое ожидание М (Х), дисперсию D (X), центральный момент |Ыз (Х); в) вероятность Р (с/2 < X < с) и показать ее на данном в условии графике ф (дг) и построенном графике F (x).

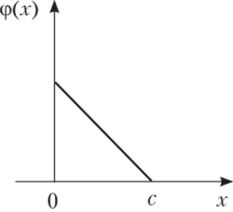
Рис. 3.21.

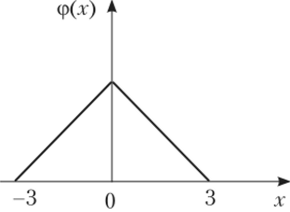
Рис. 3.22.

3.72. Случайная величина X распределена по закону Симпсона (равнобедренного треугольника) па отрезке [-3; 3] (рис. 3.22). Найти: а) выражения плотности вероятности ф (.г) и функции распределения F (x); б) числовые характеристики М (Х), D (X), Цз (Х); в) вероятность Р (-3/2 < X < 3) и показать ее на данном в условии графике ф (х) и построенном графике F (x).