Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном а

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение G неизвестно. Требуется оценить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором а предполагалось известным.

Оказывается, что по данным выборки можно построить случайную величину (ее возможные значения будем обозначать через t)

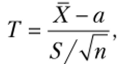
которая имеет распределение Стьюдента с k = п — 1 степенями свободы (см. пояснение в конце параграфа); здесь X — выборочная средняя, S— «исправленное» среднее квадратическое отклонение, п — объем выборки.

Плотность распределения Стьюдента.

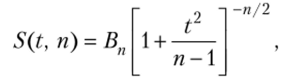
о Г (я/2).

где В_п = -.

yjn (n — 1) Г ((и -1)/2).

Мы видим, что распределение Стьюдента определяется параметром п — объемом выборки (или, что-то же, числом степеней свободы к = п — 1) и не зависит от неизвестных параметров а и а; эта особенность является его большим достоинством. Поскольку S (t_} п) — четная функция от U вероятность осуществления неравенства ^ % < у определяется так (см. гл. 11, § 2, замечание):

S / Vп

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">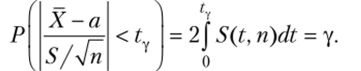

Заменив неравенство в круглых скобках равносильным ему двойным неравенством, получим Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал [хt^s/yfn., J+ ?_ys/V/zj, покрывающий неизвестный параметр а с надежностью у. Здесь случайные величины X и S заменены неслучайными величинами х и 5, найденными по выборке. По таблице приложения 3 по заданным п и у можно найти t.

Y.

Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема п- 16 найдены выборочная средняя х = 20,2 и «исправленное» среднее квадратическое отклонением = 0,8.

Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.

Решение. Найдем t. Пользуясь таблицей приложения 3, по у = 0,95 и п = 16 находим ?_у =2,13.

Найдем доверительные границы:

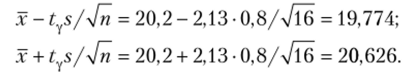
Итак, с надежностью 0,95 неизвестный параметр а заключен в доверительном интервале 19,774 < а < 20,626.

Замечание. Из предельных соотношений.

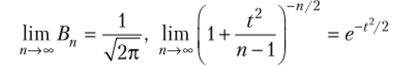
следует, что при неограниченном возрастании объема выборки п распределение Стьюдента стремится к нормальному. Поэтому практически при п > 30 можно вместо распределения Стыодснта пользоваться нормальным распределением.

Однако важно подчеркнуть, что для м, а л ы х выборок (п < < 30), в особенности для малых значений п, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т. е. к повышению точности оценки. Например, если п = 5 и у=0,99, то, пользуясь распределением Стьюдента, найдем ?_у = 4,6, а используя функцию Лапласа, найдем ?_у = 2,58, т. е. доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента.

То обстоятельство, что распределение Стьюдента при малой выборке дает не вполне определенные результаты (широкий доверительный интервал), вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется, содержит малую информацию об интересующем нас признаке.

Пояснение. Ранее было указано (см. гл. 12, § 14), что если Z — нормальная величина, причем M (Z) = 0, a (Z) = 1, а V— независимая от Z величина, распределенная по закону %² с k степенями свободы, то величина.

распределена по закону Стьюдента с k степенями свободы.

Пусть количественный признак X генеральной совокупности распределен нормально, причем М (Х) = а, о (Х) = а. Если из этой совокупности извлекать выборки объема п и по ним находить выборочные средние, то можно доказать, что выборочная средняя распределена нормально, причем (см. гл. 8, § 9).

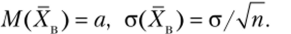
Тогда случайная величина.

также имеет нормальное распределение как линейная функция нормального аргумента X (см. гл. 12, § 10, замечание), причем M (Z) = 0, a (Z) = l.

Доказано, что случайные величины Z и.

независимы (S² — исправленная выборочная дисперсия) и что величина Vраспределена, но закону %² с k = п — 1 степенями свободы. Следовательно, подставив (**) и (***) в (*), получим величину.

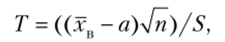
которая распределена по закону Стыодента с k = п — 1 степенями свободы.