Примеры решения задач

Задача 2.1. Принцип Ферма — постулат, сформулированный в 1662 г. II. Ферма, предписывающий лучу света двигаться из начальной точки в конечную по пути, минимизирующему время движения. Принцип Ферма справедлив не только для простейших примеров отражения и преломления света. С помощью этого принципа можно понять и точно рассчитать механическое движение.

Пункт Л находится на асфальтированной площадке, пункт В — на примыкающем к нему земляном поле, на котором скорость машины в п раз меньше. Для того чтобы за кратчайшее время добраться из А в В, был выбран оптимальный маршрут, показанный на рисунке. Найти соотношение между синусами углов аир.

ваемое на путь АО, равно: t_x = —-.

о Время ь" затрачиваемое на путь ОВ> преодолеваемый со скоростью nJll +{Lх)²

v/я, равно: /₂ = —-.

и Полное время в пути t = /, +t₂ = — (у//^ + .v² + n^l²_B + (L-x)² j.

Поскольку точка О была выбрана так, что на путь затрачивалось минимальное время, должна быть равна нулю производная времени t по расстоянию х:

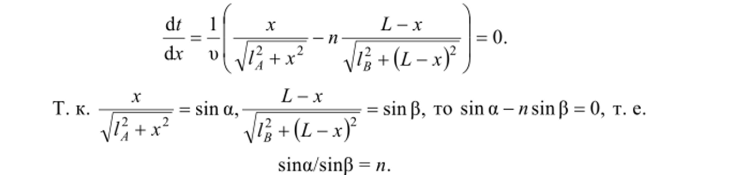
Сходство с известным законом преломления света на границе двух сред не случайно: природа устроена так, что свет выбирает оптимальный путь.

Ответ: sina/sin|3 = п.

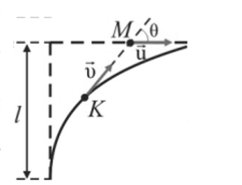
Задача 2.2*. Кошка и мышка. Кошка К преследует мышь М (см. рис.), бегущую по прямой линии с постоянной скоростью и = const. Скорость кошки по модулю и > |м| постоянна и направлена на мышь. В начальный момент скорости кошки и мыши перпендикулярны, а расстояние между ними /. Найти, через какое время кошка догонит мышь.

Решение. Обозначим г и 0 расстояние между мышыо и кошкой и угол между скоростью кошки и скоростью мыши (отсчитывается от направления скорости кошки). Записывая относительную скорость и_отн = -о + и в полярной системе координат с началом в точке нахождения кошки, получаем.

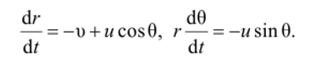
Отсюда следует, что — (и cos 0 + о) — г— и sin 0 = и²-и² или d/ d/.

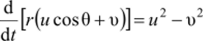
Интегрируя обе части этого уравнения в пределах от 0 до / и учитывая, что г (0) = /, 0(о)=я/2, получаем.

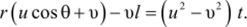
Кошка догонит мышь тогда, когда г = 0, и, следовательно, затрачи;

о/.

ваемое для этого время равно: t =.

У)

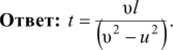
Задача 2.3. Рассмотреть движение тела, брошенного под углом, а к горизонту с начальной скоростью б₀. Найти: уравнение траектории движения; время полета тела; время подъема на максимальную высоту; максимальную высоту подъема; максимальную дальность полета и угол подъема при этом.

Решение. При отсутствии сопротивления воздуха движение будет происходить по траектории, изображенной на рисунке.

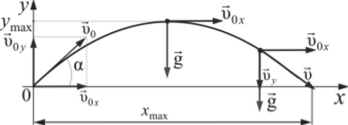
Движение данного тела можно представить как результат наложения двух одновременных прямолинейных движений по осям Ох и Оу₉ направленных вдоль поверхности Земли и по нормали к ней.

По оси Ох движение равномерное с постоянной скоростью:

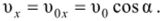
Воспользовавшись формулой для равномерного прямолинейного движения, запишем уравнение движения тела вдоль оси Ох:

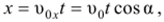
где t — время движения.

По оси Оу движение равнопеременное с ускорением а_у = - g и с начальной скоростью.

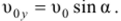
Для равномерного движения запишем:

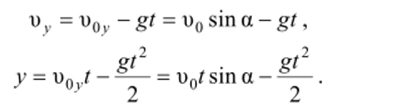
Исключив время t из уравнений движения, найдем уравнение траектории:

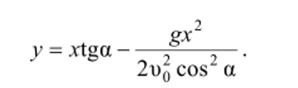
Это уравнение параболы.

В момент падения тела на Землю координата^ = 0. Тогда найдем время полета.

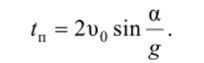aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">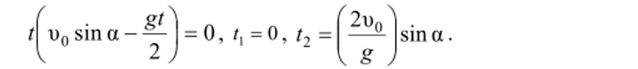

Значение времени t = 0 соответствует точке бросания тела. Таким образом, время полета тела При подъеме тела значение скорости )_у уменьшится и при v_max превращается в ноль. Из уравнения ь_у = u_0v — gt = u₀sina — gt, при o_v = 0,.

находится время подъема тела на максимальную высоту:

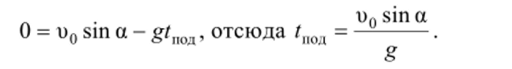
Сопоставляя выражения, видим, что время подъема тела на высоту Утах равно времени спуска его с этой высоты.

Подставив время подъема *_Под в формулу у = )_0vt — gt²/2 =

= о₍₎/ sin a — gt²/2, найдем максимальную высоту подъёма тела:

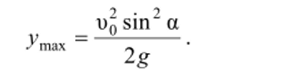
Дальность полета дг_тах определяется, если в уравнения Л' = и_0г/ = о₀/ cos, а вместо t подставить время полета:

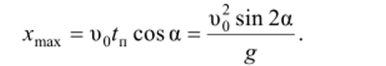
Дальность полета максимальна, когда значение sin2a максимально:

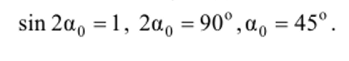
Задача* 2.4. Парабола безопасности. Из начала координат под углом, а к горизонтальной оси х бросают камень со скоростью и. Сопротивлением воздуха можно пренебречь. При каком угле а₍₎ камень попадет в точку с координатами х₀, у₀ (см. рис.)?

Решение. Радиус-вектор камня в момент времени t дается формулой r = ut + gt²f 2, где g — вектор ускорения свободного падения, направленный вертикально вниз. Ориентируя ось у вверх, запишем уравнение в координатах: x = ut cos а, у = м/sin a-gt²12.

Исключив /, найдем уравнение траектории: у = xtga — gx² /(2м² cos² а).

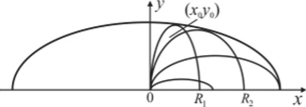
Из этого уравнения, при у = у₀, х = х₀, находим.

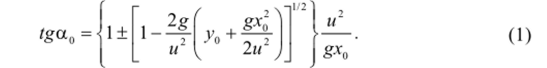
Действительно значения oto, определяющие возможные траектории, получаются лишь при условии неотрицательности выражения под знаком квадратного корня, т. с. при условии.

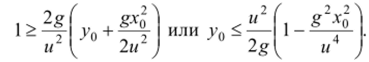
Таким образом, при начальной скорости и камнем могут быть достигнуты лишь точки, лежащие ниже точек параболы,.

называемой параболой безопасности.

Точки, лежащие вне ограничиваемой этой параболой области, не могут быть достигнуты.

Достаточно обсудить лишь область .v₀ >0, у₀ > 0. Из (2) видно, что u²/(gx₀)> 0. Эго в сочетании с (1) означает, что по крайней мере одно значение ао больше или равно я/4. Точка на параболе безопасности может быть достигнута лишь при одном значении а₀ > я/4, а точки ниже параболы безопасности — при двух значениях: aoi и Оо2- Расстояния, на которых соответствующие траектории пересекут горизонтальную плоскость, равны R = w"sin2aoi/g, R2 ⁼ w" sin2ao2/g.

Задача 2.5. С какой скоростью и по какому курсу должен лететь самолет, чтобы за 2 часа пролететь точно на север 720 км, если во время полета дует постоянный северо-западный ветер под углом 30° к меридиану со скоростью 36 км/ч? Ответ представить в км/ч.

дано:

t = 2 ч.

S = 720 км/ч Р = 30° и = 36 км/ч.

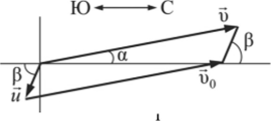
Решение. Чтобы попасть в пункт назначения, самолету необходимо лететь под углом а к меридиану, отклоняясь на запад.

Обозначим искомую относительную скорость как и, а результирующую абсо.

и.

—? а — ?

лютную скорость, направленную вдоль меридиана, как н₀. Её модуль )₀ = S/t. Из рисунка видно, что н_у = и + и . Модуль скорости |н| найдем из векторного треугольника скоростей, используя теорему косинусов:

Таким образом, скорость полета самолета больше н₀.

Угол отклонения, а от курса можно найти по теореме синусов:

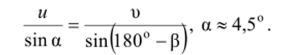
Ответ: и = 392 км/ч; а «4,5°.