Метод Монте-Карло. 
Надежность и безопасность программного обеспечения

Пусть задана вероятностная модель функционирования системы с целью нахождения некоторой усредненной характеристики а [23— 25]. Эта модель есть представление любого показателя безопасности через некоторые случайные величины Z =f (z_v …, z"). Тогда.

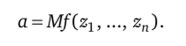
Здесь М — оператор вычисления математического ожидания.

Величины z_b …, z_n имеют реальный смысл: это длительности безотказной работы элементов системы, количество искаженных бит информации в канале и т. п. В качестве функций/(г_1; …, z_n) могут выступать различные функции, зависящие от искомого показателя безопасности. Если определяется вероятность, то.

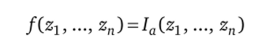
есть индикаторная функция некоторого события, связанного с показателем а. Если определяется среднее время до отказа, то.

Зная распределения величин z_1; …, z," найденные статистическим путем, и воспроизведя их реализации в точном соответствии с этими распределениями, получим реализацию показателя z. Повторяя опыт всякий раз со значениями z_b независимыми от предыдущих значений (случайной величины z), получаем независимые реализации Z_b …, Z_N случайной величины z, по которым находим усреднением оценку величины а. Если П — пространство возможных значений случайного вектора z = (Zj, z"), а р (х) — его плотность распределения в этом пространстве, то можно записать.

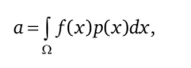
где х = (х_1} х_п); dx — элемент объема пространства Q.

Иначе можно сказать, что /(z) есть несмещенная оценка параметра а. Если искомый показатель является вероятностью некоторого события, то функция/(z) является индикаторной. В данном случае при проведении моделирования используется следующая формула для расчета параметра а:

где N — число опытов или реализаций вектора z, который имеет распределение р (х); I_a(z) — индикаторная функция, принимающая значение 1, если событие, соответствующее показателю а, произошло, и О в противном случае.

Таким образом, для вычисления вероятностного показателя а необходимо заданное число раз (N) генерировать случайный векторгв соответствии с его распределением р (х). При натурных испытаниях вектор z реализуется как объективный результат ошибок, помех, отказов и сбоев. При имитационном моделировании данный вектор генерируется датчиком псевдослучайных чисел с помощью программных или аппаратных средств.

Данный подход является обычным методом имитационного моделирования Монте-Карло и требует большого количества реализаций случайного вектора при малых искомых вероятностях. Для ускорения имитационного моделирования разработан ряд методов, например, модифицированный метод Монте-Карло, метод взвешенного моделирования (значимой выборки), метод дополняющих переменных и др.

Существуют и другие методы понижения дисперсии, например метод расслоенной или стратифицированной выборки. Однако многие из этих методов требуют наличия достаточно детального описания моделируемой системы и ее особенностей, что в ряде случаев затрудняет их применение. Кроме того, достоинства названных методов уступают достоинствам метода значимой выборки, который показал свою эффективность при моделировании многих систем. Основная цель всех этих методов состоит в понижении дисперсии моделируемой на выходе системы случайной величины. Уменьшение разброса характеристик выходного параметра позволит сократить необходимое для заданной достоверности число реализаций случайного вектора и, следовательно, ускорить имитационное моделирование. Рассмотрим суть ускоренного моделирования на примере метода значимой выборки.