Теория радиоактивного б — распада

Известно, что многие радиоактивные элементы распадаются, испуская б — частицы. По вылете из атомного ядра б — частица, имея двукратный положительный заряд (+2е), ускоряется в кулоновском поле атомного ядра, заряд которого обозначим через Ze(под Zбудем подразумевать номер элемента после вылета б — частица, Z= Z' — 2, если Z' есть номер элемента до радиоактивного распада).

Большая прочность б — частицы позволяет предполагать, что она существует в ядре в виде самостоятельного объекта, являясь одним из простых образований, из которых строится атомное ядро. Ясно, что б — частицы может длительно находиться в атомном ядре лишь в том случае, если область вблизи атомного ядра является минимумом потенциальной энергии б — частицы. Кулоновская потенциальная энергия б — частицы, равная 2Ze²/r, где r — расстояние от ядра до частицы, по мере приближения к ядру, как это изображено на рис. 5.1 пунктирной кривой, все время возрастает монотонно. Поэтому минимум энергии вблизи ядра может получиться лишь в том случае, если на близких расстояниях на б — частицы действуют какие-то иные силы, по мимо электрических. Такими силами являются ядерные силы, действующие между нуклонами. Эти силы весьма велики и действуют лишь на очень малых расстояниях. Именно этими силами и обусловливается смена кулоновского отталкивания на резкое притяжение вблизи ядра, изображенное на рис. 5. 1 сплошной кривой. Такое поведение потенциала называют образованием потенциальной ямы или, кратера. При наличии таких сил б — частицы, находящаяся в области r₀, т. е. в поле сил притяжения, будет длительно удерживаться внутри ядра.

Как же происходит б — распад? Долгое время это оставалось загадкой. Еще Кельвин предполагал, что частицы, испускаемые радиоактивным элементом, как бы кипят внутри потенциального кратера. Время от времени одна из частиц получает избыток — энергии над средней, преодолевает барьер и, вылетев за него, ускоряется отталкивательным полем, приобретая большую энергию.

Однако эта наглядная картина, как было показано Резерфордом, противоречит опыту. Резерфорд бомбардировал атомы радиоактивного урана бчастицами тория С'. Энергия бчастиц тория С' равна 13 · 10 ^-6 эрг. Такие частицы, преодолевая кулоновское отталкивание, могут весьма близко подойти к ядру. Оценим расстояния наибольшего сближения r₁.Очевидно, что r₁есть то расстояние, при котором потенциальная энергия частицы 2Z'e²/r₁будет равна исходной кинетической, т. е. 2Z'e²/r₁ = 13· 10 ^-6эрг,: Z' есть номер урана и равен 92. Поэтому мы находим, что r₁= 3−10-¹²см.

Наблюдение показывает, что рассеяние таких частиц строго такое, каким оно должно быть при действии на б — частицы кулоновского поля. Это означает, что ядерные силы начинают действовать на б — частицы расстояниях меньших, нежели 3 · 10 ^-12 см. Поэтому бчастицы, заключенные в ядре, находятся внутри области, радиус которой меньше 3 * 10^-12см.

С другой стороны, уран сам является радиоактивным элементом и испускает бчастицы. Измерение энергии этих частиц показывает, что она равна 6,6 · 10^-6эрг.

Эти бчастицы вылетают из ядра, т. е. с расстояний, меньших 3 · 1О^-12см. Тогда, ускоряясь в кулоновском поле, они должны были бы приобрести энергию, равную высоте потенциального барьера (см. рис. 5. 1) и во всяком случае большую, нежели, 13 · 10 ^-6 эрг. Получается же так, как если бы они вылетали с расстояния r = 6 · 10 ^-12см. Таким образом, опыт приводил с точки зрения классической физики к парадоксальному положению: нужнобыло предположить, что кулоновское электрическое поле ядра действует на падающие извне б — частицы, но не действует на вылетающие на ядра, либо считать, что закон сохранения энергии не выполняется при радиоактивном распаде.

Решение этого парадокса вытекает из квантовой механики, приводящей к возможности туннельного эффекта через потенциальный барьер, разделяющий область притяжения (r₀) от области отталкивания (r> г₀).

В самом деле, тогда парадокс полностью решается: частица, находящаяся внутри ядра, может иметь энергию, меньшую, нежели высота барьера, и все же пройти через него. Частица же, пролетающая извне, ввиду малой прозрачности барьера лишь в очень редких случаях будет захватываться ядром (так как время пребывания ее около ядра очень — мало). Поэтому рассеяние б — частиц, падающих извне, будет обусловливаться кулоновскими силами, действующими за пределами барьера. Предположенная малая прозрачность барьера, согласуется с тем фактом, что периоды радиоактивного б — распада весьма велики.

Применяя теорию прохождения через потенциальные барьеры, легко облечь изложенную идею в математическую форму и найти выражение для константы радиоактивного распада л — эта константа определяется следующим образом. Если имеющееся к моменту времени t число не распавшихся атомов N, то dN будет равно.

(5.1).

Для вычисления константы распада л мы можем применить квантовую теорию просачивания частиц через потенциальные барьеры, изложенную в предшествующем параграфе. Согласно этой теории б — частицу внутри ядра следует рассматривать как находящуюся в «квазистационарном» состоянии. Обозначая скорость частицы в этом состоянии через х_i,-, радиус барьера через r₀и его коэффициент прозрачности через D, мы получим.

(5.2).

Остается вычислить D. Ввиду более сложной формы барьера вместо (4.24) мы получим (см. (1.24)).

(5.3).

Из рис. 5.1 следует, что первая точка поворота r^'₁есть г₀ (радиус ядра), вторая (г₂) определится из условия.

(5.4).

Таким образом,.

(100.5).

Вводя сюда новую переменную %, мы получаем.

(5.5').

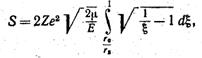
и, полагая, наконец, ещеm о = cos²u, мы без труда вычислим порученный интеграл.

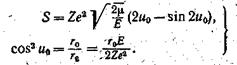
(5.5').

Воспользуемся тем, что отношение меньше, единицы, и {разложим Uо и sin2 Uо в ряд по степеням (достаточно ограничиться двумя первыми членами). Тогда мы получим.

. (5.7).

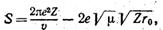
где х — скорость вдали от ядра, равная. Итак, выражение для константы распада (5.3) раскрывается слёдующим образом:

(5.8).

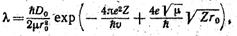
Или.

(5.9).

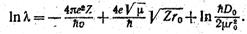
Наиболее замечательным выводом из этой формула является зависимость между л и скоростью л — частицы v. Подобная зависимость еще задолго до квантовой теории этого явления была установлёна на опыте Гайгером и Нэттолом.

Далее мы видим, что 1nл зависит от номера элемента Z (Z= Z'— 2) и радиуса ядра.

Из опыта известно, что константы распада варьируются в очень |широких пределах: от 10⁶сек^-1до 10^-18сек^-1. Если бы в таких же пределах приходилось варьировать параметры, определяющие л, то теория была бы наверно неправильной. Замечательным следствием формулы (5.9) является то, что если по эмпирическим данным для лопределять радиусы ядер, то окажется, что они все лежат в тесных границах, примерно от 5 · 10 ^-12см до 9 · 10^-12см. Значительное различие в величине л для разных элементов определяется не различием в радиусах ядер, а различием в энергии вылетающих частиц. Слабую зависимость л от r₀ и резкую от vследует рассматривать как подтверждение теории.