Независимые факторы. 
Описательная статистика

Если не выполняется 2-я гипотеза, и некоторые из переменных z линейно зависят от других, то матрица M вырождена, и использование приведенного оператора оценивания невозможно.

Вообще говоря, предложить метод оценивания параметров регрессии в этом случае можно. Так, пусть множество независимых факторов разбито на две части (в этом фрагменте используются обозначения сокращенной формы уравнения регрессии):

,.

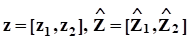
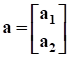
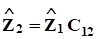
и .

Тогда можно записать уравнение регрессии в форме.

+ e,.

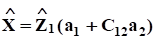
и оценить линейную комбинацию параметров (предполагая, что столбцы Z₁ линейно независимы). Но чтобы оценить сами параметры, нужна априорная информация, например: .

Однако вводить в регрессию факторы, которые линейно зависят от уже введенных факторов, не имеет смысла, т.к. при этом не растет объясненная дисперсия (см. ниже).

На практике редко встречается ситуация, когда матрица M вырождена. Более распространен случай, когда она плохо обусловлена (между переменными Z существуют зависимости близкие к линейным). В этом случае имеет место мультиколлинеарность факторов. Поскольку гипотеза 2 в части отсутствия ошибок измерения, как правило, нарушается, получаемые (при мультиколлинеарности) оценки в значительной степени обусловлены этими ошибками измерения. В таком случае (если связь существует), обычно, факторы по отдельности оказываются незначимыми по t-критерию, а все вместе — существенными по F-критерию. Поэтому в регрессию стараются не вводить факторы сильно скоррелированные с остальными.

В общем случае доказывается, что.

.

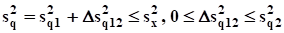
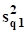
где и — дисперсии, объясненные факторами z₁ и z₂ по отдельности;

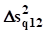
— прирост объясненной дисперсии, вызванный добавлением в регрессии факторов z₂ к факторам z₁.

В соотношении для прироста объясненной дисперсии:

— левая часть выполняется как строгое равенство, если и только если.

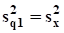
(коэффициент детерминации в регрессии по z₁ уже равен единице), или вектор остатков в регрессии по z₁ ортогонален факторам, т. е. имеет с ними нулевую корреляцию (возможное влияние факторов z₂ уже «приняли» на себя факторы z₁), или факторы линейно зависят от факторов ;

— правая часть выполняется как строгое равенство, если и только если факторы ортогональны факторам .

Если в множество линейно независимых факторов добавлять новые элементы, то коэффициент детерминации растет вплоть до единицы, после чего рост прекращается. Своего максимального значения он обязательно достигнет при n = N (возможно и раньше) — даже если вводимые факторы не влияют по-существу на изучаемую переменную. Поэтому сам по себе коэффициент детерминации не может служить статистическим критерием «качества» уравнения регрессии. Более приемлем в этой роли коэффициент детерминации, скорректированный на число степеней свободы:

.

который может и уменьшиться при введении нового фактора. Точную же статистическую оценку качества (в случае нормальности распределения остатков) дает F-критерий. Однако учитывая, что значения F^c оказываются несопоставимыми при изменении n (т.к. получают разное число степеней свободы), наиболее правильно эту роль возложить на уровень ошибки ^с для F^c.

В результате введения новых факторов в общем случае меняются оценки параметров при ранее введенных факторах:

.

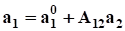
где — оценка параметров регрессии по z₁ (до введения новых факторов);

A₁₂ — матрица, столбцы которой являются оценками параметров регрессии переменных z₂ по z₁.

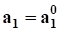
«Старые» оценки параметров сохраняются (), если и только если.

— коэффициент детерминации в регрессии по z₁ уже равен единице, или вектор остатков в регрессии по z₁ ортогонален факторам (в этих двух случаях a₂ = 0), или факторы ортогональны факторам (в этом случае A₁₂ = 0).

Итак, возникает проблема определения истинного набора факторов, фигурирующих в гипотезе 1, который позволил бы найти оценки истинных параметров регрессии. Определение такого набора факторов есть спецификация модели. Формальный подход к решению этой проблемы заключается в поиске так называемого наилучшего уравнения регрессии, для чего используется процесс (метод) шаговой регрессии.

Пусть z — полный набор факторов, потенциально влияющих на x. Рассматривается процесс обращения матрицы ковариации переменных [x, z]. В паре матриц (n+1)(n+1)

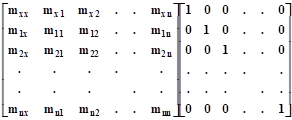
делаются одновременные преобразования их строк в орты. Известно, что, если 1-ю матрицу преобразовать в единичную, то на месте 2-й матрицы будет получена обратная к 1-й (исходной). Пусть этот процесс не завершен, и только несколько строк 1-й матрицы (но не ее 1-я строка) преобразованы в орты. Это — ситуация на текущем шаге процесса.

На этом шаге строкам-ортам в 1-й матрице соответствуют включенные в регрессию факторы, на их месте в 1-й строке этой матрицы оказываются текущие оценки параметров регрессии при них. Строкам-ортам во 2-й матрице соответствуют невведенные факторы, на их месте в 1-й строке 1-й матрицы размещаются коэффициенты ковариации этих факторов с текущими остатками изучаемой переменной. На месте m_xx показывается текущее значение остаточной дисперсии.

На каждом шаге оцениваются последствия введения в регрессию каждого не включенного фактора (преобразованием в орты сответствующих строк 1-й матрицы) и исключения каждого введенного ранее фактора (преобразованием в орты соответствующих строк 2-й матрицы). Выбирается тот вариант, который дает минимальный уровень ошибки ^с для F^c. Процесс продолжается до тех пор, пока этот уровень сокращается.

Иногда в этом процессе используются более простые критерии. Например, задается определенный уровень t-статистики (правильнее — уровень ошибки ^с для t^c), и фактор вводится в уравнение, если фактическое значение t^c для него выше заданного уровня (ошибка ^с ниже ее заданного уровня), фактор исключается из уравнения в противном случае.

Такие процессы, как правило, исключают возможность введения в уравнение сильно скоррелированных факторов, т. е. решают проблему мультиколлинеарности.

Формальные подходы к спецификации модели должны сочетаться с теоретическими подходами, когда набор факторов и, часто, знаки параметров регрессии определяются из теории изучаемого явления.

Прогнозирование

Требуется определить наиболее приемлемое значения для x_N+1 (прогноз), если известны значения независимых факторов (вектор-строка):

.

— истинное значение искомой величины;

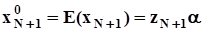
— ожидаемое значение;

— искомый МНК-прогноз.

Полученный прогноз не смещен относительно ожидаемого значения:

.

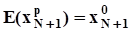
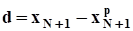
и его ошибка имеет нулевое матожидание:

E (d) = 0,.

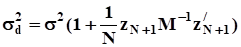
и дисперсию, которая минимальна в классе линейных оценок .

Оценка стандартной ошибки прогноза при n = 1 рассчитывается по формуле.

.