Влияние кривизны поверхности на равновесие фаз

До сих пор мы рассматривали поверхностные явления в системах, в которых сосуществующие фазы разделены плоской или практически плоской (с большим радиусом кривизны) межфазной границей. Искривление поверхности раздела фаз вносит существенные изменения в термодинамические свойства системы и обусловливает некоторые важные эффекты, относящиеся к числу капиллярных явлений. Для высокодисперсных систем характерна большая кривизна поверхностей раздела фаз, поэтому необходимо учитывать ее влияние на термодинамические свойства таких систем.

ЗАКОН ЛАПЛАСА

Давления в контактирующих фазах, разделенных плоской поверхностью, в условиях равновесия одинаковы. В отличие от этого давления в фазах, разделенных искривленной, например сферической, поверхностью, отличаются. В этом легко убедиться на примере мыльного пузырька, выдутого на трубочке: если оставить отверстие трубочки открытым, то под действием избыточного (по сравнению с атмосферным) давления в пузырьке воздух будет выходить, а размеры пузырька будут уменьшаться вплоть до его полного исчезновения. При этом происходит уменьшение поверхности пузырька и связанной с поверхностями пленки поверхностной энергии. Что избыточное давление возрастает с уменьшением радиуса пузырька, т. е. радиуса кривизны межфазной поверхности, можно доказать, если выдуть два пузырька разных размеров и затем соединить их: маленький пузырек будет уменьшаться, а большой увеличиваться до полного перехода воздуха из малого пузырька в большой.

Чтобы получить связь избыточного давления под искривленной поверхностью с ее поверхностным натяжением и радиусом кривизны, рассмотрим условия равновесия между каплей радиуса г и большим объемом пара при постоянных в каждой фазе давлении и температуре. Пусть вблизи равновесия небольшое число молекул, отвечающее увеличению радиуса капли на 6 г, переходит из пара в каплю; давление, а следовательно, и химический потенциал вещества остаются при этом практически постоянными. Условие близости системы к равновесию, т. е. к минимуму ее термодинамического потенциала §, записывается в виде равенства нулю первой вариации Ь§:

где АР = р' — р" — разность давлений в капле р' ив паре р" V — объем капли; 5 — поверхность капли.

Гиббс показал, что существует определенное положение разделяющей поверхности, для которого 6а = 0; это так называемая поверхность натяжения. Для поверхности натяжения можно записать:

Для сферических частиц радиуса г имеем 65 = 8я/6г и 6 К= 4я^6г. Соответственно выражение для избыточного давления Ар, создаваемое искривленной поверхностью, принимает вид:

Это соотношение называют законом Лапласа. Величину Ар = р_а — разность давлений в соседних фазах, разделенных искривленной поверхностью, называют капиллярным давлением.

В рассмотренном случае (капля в паре) давление в капле повышено по сравнению с давлением в паре на 2а/r, для обратного случая (пузырек пара в жидкости) давление на ту же величину больше в паре, чем в жидкости.

Капиллярное давление можно рассматривать как добавку, которая в зависимости от знака кривизны увеличивает или уменьшает внутреннее давление К по сравнению с внутренним давлением при наличии плоской поверхности раздела т. е. %® —⁽Kq± IpJ.

Для капли воды радиусом 1 мкм капиллярное давление р₀ составляет 2а/г * 1,5 • 10⁵Па (1,5атм), т. е. ~ 0,1% по сравнению с внутренним давлением воды, оцениваемым как а/b ~ 2 • 10⁸ Па (2000 атм); для капель размером 10 нм значениер_а достигает уже — 10%от!К.

В соответствии с уравнением Лапласа действие силового поля искривленной поверхности на соприкасающиеся фазы аналогично действию упругой пленки с натяжением а, расположенной в поверхности натяжения. При этом следует помнить, что свойства поверхностного слоя принципиально отличаются от свойств упругой пленки: поверхностное натяжение о не зависит от ее площади 5, тогда как натяжение упругой пленки растет по мере ее деформации .^[1]

При рассмотрении искривленных границ между фазами различные разделяющие поверхности перестают быть эквивалентными друг другу. В данном случае нас интересует не только величина о, но, как видно из уравнения Лапласа, и радиус кривизны разделяющей поверхности г, который зависит от выбора ее расположения. Положение разделяющей поверхности, эквивалентное реальному поверхностному слою как по величине а, так и по координате ее «приложения*, было введено Гиббсом как «поверхность натяжения». При больших радиусах кривизны поверхности, с учетом малой толщины поверхности разрыва, различием в радиусах поверхности натяжения и других возможных разделяющих поверхностей (например эквимолекулярной поверхности, см. гл. II), как правило, можно пренебречь.

Закон Лапласа является основным в теории капиллярности. В общем случае (для несферических поверхностей) он может быть записан в виде.

где г, и г₂ — главные радиусы кривизны поверхности.

В простейшем случае сферической поверхности (пузырек или капля жидкости в невесомости) оба главных радиуса кривизны одинаковы и постоянны вдоль всей поверхности. Для малых капель и пузырьков форма, близкая к сферической, сохраняется и в поле силы тяжести; это справедливо при соблюдении условия р_а = 2о/г" «r (p' - p»)g, т. е. ? «а² = 2а/(р' — р»)& где р' и р" — плотности жидкой фазы и газа соответственно; g — ускорение силы тяжести; величина а — капиллярная постоянная.

Если данное условие не соблюдается, то форма поверхности отклоняется от сферической. При этом капля остается симметричной относительно вертикальной оси, т. е. имеет форму тела вращения. Капиллярное давление в такой капле (пузырьке) меняется с высотой: перепаду высот Az отвечает разность капиллярных давлений Л/?₀, равная.

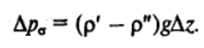
Как известно из аналитической геометрии, главные радиусы кривизны поверхности вращения лежат в той же плоскости, что и ось вращения Oz (например, в плоскости xOz на рис. 1.27). Они связаны с формой сечения поверхности тела вращения плоскостью xOz соотношениями.

Заменяя в уравнении Лапласа главные радиусы кривизны этими выражениями и учитывая зависимость капиллярного давления от вертикальной координаты г, получа;

Рис. 1-27. Равновесная форма капли (или пузырька) на твердой подложке.

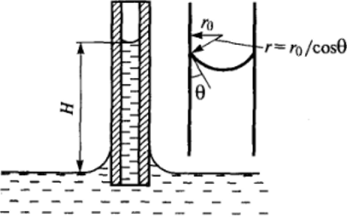
Рис. 1-28. Поднятие жидкости в смачиваемом капилляре.

ют дифференциальную форму уравнения Лапласа. Численное интегрирование такого дифференциального уравнения дает строгое математическое описание поверхности равновесной большой капли или пузырька, а также капиллярного мениска в поле силы тяжести. Определение равновесной формы поверхности лежит в основе ряда методов измерения поверхностного натяжения легкоподвижных границ раздела фаз жидкость — газ и жидкость — жидкость (см. 1.6).

Остановимся на некоторых характерных примерах возникновения капиллярного давления при контакте жидкости с твердыми телами различной формы.

Рассмотрим поведение жидкости в тонком капилляре, опущенном в жидкость; в этом случае можно считать, что мениск имеет сферическую форму (рис. 1−28). При условии смачивания жидкостью стенок капилляра (острый краевой угол 0) ее поверхность будет искривленной с отрицательным радиусом кривизны г (вогнутый мениск). В результате давление в жидкости под поверхностью мениска оказывается пониженным по сравнению с давлением под плоской поверхностью на 2а/г. Жидкость будет подниматься по капилляру до тех пор, пока капиллярное давление не уравновесится гидростатическим давлением столбика поднявшейся жидкости, т. е.

где р' и р" — плотности жидкости и ее насыщенного пара (или воздуха); g — ускорение силы тяжести; Н — высота подъема жидкости.

Кривизна поверхности жидкости в капилляре определяется условиями смачивания, т. е. значением краевого угла 0. Радиус кривизны мениска г связан с радиусом тонкого капилляра соотношением.

r= гъ/cos 0. Высота капиллярного поднятия приближенно определяется формулой Жюрена^[2]:

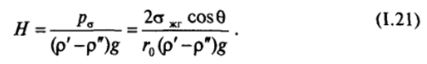
Чем лучше жидкость смачивает стенки капилляра, тем выше поднятие жидкости в нем при данном значении а*г. При несмачивании (0 > 90°) жидкость в капилляре образует выпуклый мениск; этому отвечает повышение давления в жидкости под поверхностью мениска, и вместо поднятия уровня жидкости имеет место опускание (по сравнению с плоской границей раздела).

Роль капиллярных явлений в природе и технике огромна. Ими обусловлено проникновение жидкости по тонким каналам в почвах, растениях, горных породах, пропитка пористых материалов и тканей, изменение структурно-механических свойств почв и грунтов при их увлажнении и т. п.

На проявлении капиллярного давления основана ртутная порометрия — метод, широко используемый для определения объема пор и их распределения по размерам в различных пористых материалах: керамике, углях, адсорбентах, катализаторах. Ртуть очень плохо смачивает неметаллические поверхности, поэтому при внедрении ртути в пору возникает «противодействующее» капиллярное давление, которое с достаточной точностью можно считать равным 2a/r (г — радиус поры или средний радиус для пор сложной формы). Изучая зависимость объема ртути, проникающей в данную навеску порошка, от прилагаемого давления, можно получить кривую распределения пор по размерам. Для внедрения ртути в тела с очень тонкими порами, в десятки и единицы нанометров, капиллярное давление ртути, которое должно преодолеваться приложенным давлением, достигает 10⁸ + 10⁹ Па (10³+ 10⁴ атм).

Интересным примером проявления капиллярного давления может служить возникновение капиллярной стягивающей силы между частицами при наличии мениска — «манжеты» смачивающей жидкости в месте их контакта (рис. 1−29). Мениск между сведенными до соприкосновения частицами радиуса го представляет собой поверхность вращения, характеризующуюся в каждой точке двумя радиусами кривизны (на рис. 1−29, а противоположного знака г > 0 и гг < 0),.

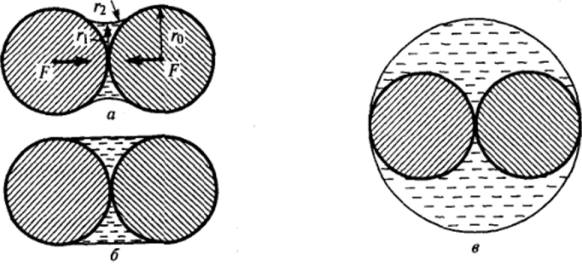
Рнс. 1−29. К расчету капиллярной стягивающей силы F мениска в зависимости от его формы причем /г + 1 /ri = const. Если г «по, то г и о можно считать приблизительно постоянными.

Допустим, что происходит полное смачивание. Капиллярная стягивающая сила F, которую нужно преодолеть, чтобы частицы начали отрываться друг от друга, складывается в данном случае из силы Fu вызываемой капиллярным давлением:

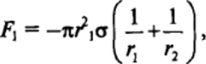
и силы F₂, обусловленной составляющей поверхностного натяжения, действующей в вертикальной плоскости симметрии:

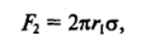
т. е.

Значение F существенно зависит от количества жидкости в мениске. По мере уменьшения объема жидкости (например, при высыхании) сила, стягивающая частицы, увеличивается и становится максимальной при «исчезающем» мениске^[3], т. е. при г -> 0. В таком случае, используя простые геометрические соотношения, имеем ъ * — п/2го и.

F~ 2nroo. При увеличении количества жидкости до образования цилиндрического мениска ъ -> со и г -+ го (рис. 1−29, б), капиллярная стягивающая сила уменьшается до F— я^о. При образовании «мениска» с параметрами г = г* = 2гъ (рис. 1−29, в) стягивающая сила исчезает, т. е. F* 0. Именно этим обусловлены известные акты «расплывания» сильно увлажненного песка и его более или менее хорошей формуемости при слабом увлажнении. Капиллярные силы во многом определяют сцепление частиц и непосредственно связанные с этим сцеплением механические свойства почв, грунтов (см. гл. IX), различных технических, пищевых, лекарственных и других порошков и паст, как готовых продуктов и материалов, так и их полуфабрикатов.

• [1] Для растворов может проявляться зависимость поверхностного натяжения отплощади поверхности, связанная с эффектом Гиббса (см. VI 1.4).
• [2] Болес точное выражение для высоты капиллярного поднятия было полученоРэлеем (см. подробнее [14]).
• [3] Надо помнить, что рассматриваемые соотношения предполагают наличиесплошной фазы и могут утрачивать справедливость, когда радиус мениска приближается к молекулярным размерам Ь уравнение Лапласа выводится в предположении г> Ь.