Анализ и учет потерь мощности при транзите электроэнергии и их распределение между участниками энергообмена

Анализ и учет потерь мощности при транзите электроэнергии и их распределение между участниками энергообмена

Работа выполнена в научном и практическом направлениях по минимизации потерь мощности при передаче электроэнергии в локальных распределительных сетях между субъектами энергообмена (производителями и потребителями), за счет энергосберегающих технологий ориентированных на технологические мероприятия, такие как модернизация и реконструкция сетей. В различных схемах электроэнергетических систем достаточно часто оказывается целесообразно передача энергии и ее мощности через промежуточные (транзитные) узлы. Структурные изменения в электроэнергетике, в настоящее время, в основном связаны с введением рыночных отношений между субъектами энергообмена, поэтому в данной работе особое внимание уделено вопросу расчета потерь мощности, поскольку именно она нелинейно зависит от мощности в узлах и ветвях сети. Следует отметить, что такими узлами в задачах транзита мощности могут быть как источники, так и потребители. Последнее потребовало необходимость поиска возможных путей снижения потерь при транспортировке энергии как за счет совершенствования и оптимизации схем распределительных сетей, так и за счет использования промежуточных транзитных узлов. Из сказанного следует, что транспортная задача в такой постановке имеет более общий характер и расширяет возможности решения задач оптимизации потерь мощности для локальных подсистем энергокластеров. В работе составлена транспортная матрица для решения задач транзита мощности, алгоритм которой с учетом отличительных особенностей, которые заключаются в использовании сквозной нумерации источников и потребителей в матрице, а любой узел может быть транзитером. При этом транзитная мощность ii-ом узле Zii=0, а размерность матрицы в отличии от ранее рассматриваемых задач имеет (n+m) (n+m) и она остается квадратной как и у всех транспортных задач линейного программирования. Транзитные переменные Xii входят в решение задачи со знаком минус, а все транзитные переменные считаются базовыми. Из приведенного примера в работе количество ветвей сети минимально, что существенно снижает затраты на строительство и содержание сети, а сам механизм расчета позволяет минимизировать потери мощности между субъектами энергообмена и, как следствие получать экономию как с позиции затрат на строительство сети, так и с позиции управления перетоками энергии в ней Одним из основных путей экономии электроэнергии во всех областях производства и ее распределения между участниками энергообмена являются энергосберегающие технологии, ориентированные на технологические мероприятия, направленные на модернизацию и реконструкцию, а также строительство энергосетей, поскольку последнее связано с транспортировкой электроэнергии, что требует дополнительных капитальных вложений. Не менее важным действием в этой части являются мероприятия, связанные с процессом управления передачи энергии.

В условиях параллельной работы энергосистем в составе их объединения, для реализации межсистемного эффекта рациональности потребления энергомощностей и энергоресурсов, а также покрытия дефицита мощности на отдельных участках локальной сети возникает необходимость в значительных перетоках энергии. В тоже время имеет место быть дополнительный технологический расход электроэнергии от транзитных перетоков, а экономия от реализации межсистемного эффекта при параллельной работе энергосистемы во всех случаях значительно превышает затраты, вызываемые потерями энергии от них.

Наряду с этим не менее важными являются вопросы совершенствования эксплуатационного обслуживания энергетических сетей, оптимизация их схем и режимов.

Известно, что одним из наиболее важных факторов при выборе энергопоставщика является цена на электроэнергию, которая на прямую зависит от величины технических потерь в локальных или глобальных электрических сетях. Очевидно, что эти потери складываются как из потерь при передаче энергии от поставщика к потребителю, так и при транспортировке для других поставщиков и энергопотребителей. Вследствие чего возрастает стоимость отпускаемой электрической энергии и, как следствие, конкурентоспособность между поставщиками. Поддержка конкуренции поставщиков на энергорынке требует не только регулировки условий деятельности на рынке услуг за счет тарифа, но и технологической оптимизации потерь при передаче от поставщика к потребителю во фрагментарных электрических сетях областных энергоснабжающих компаниях (энергокластеров). Компенсация потерь за счет тарифа на энергию, для потребителей одного лицензиата, вследствие включения в них стоимости потерь от передачи мощности других потребителей экономически несправедливо, последнее подтверждается и международной практикой. Так, в Австралии, согласно новому электроэнергетического кодексу, предусматривается обязанность крупных потребителей (максимальная мощность более 10 МВт) дополнительно к стоимости потребленной электроэнергии оплачивать и часть потерь передачи мощности этому потребителю [4].

Структурные изменения в электроэнергетике, связанные с введением рыночных отношений между субъектами энергообмена (производителями и потребителями), стало актуальным [1, 2].

В различных схемах электроэнергетических систем достаточно часто оказывается целесообразным передача энергии и её мощности через промежуточные (транзитные) узлы. Простейшие электрические схема сети поясняющие понятие «транзит мощности» это две схемы топология которых такова — имеются источники электроэнергии (U1) и два потребителя (П2, П3) напрямую соединенные с источником. Если источник передаёт всю потребляемую энергию на П2, а затем через него на П3, то мы имеем простейшую транзитную схему, в которой узел П2 является одновременно потребителем и транзитером. Рассматривая транспортную задачу с транзитом мощности, где источников m, а количество потребителей n, передача мощностей между источниками энергии и ее потребителями может быть различной, достаточно часто в настоящее время становится целесообразным использование промежуточных узлов (транзитных). Предлагаемая схема ориентирована не только на оптимизацию потерь мощности, при её транспортировке, но и на технологическую реконструкцию, которая также минимизирует экономические потери.

Из сказанного выше следует, что транспортная задача в такой постановке имеет более обобщенный характер и расширяет возможности, особенно для локальных участков энергокластера. При решении транспортной задачи с транзитом мощности одним из важных вопросов становится определение, к какому типу задач она относится.

Известно два типа задач — закрытая и открытая, с помощью которых можно рассматривать и решать такого рода задачи. В открытой форме постановки задачи с транзитом мощности, которая в отличие от закрытой для m источников и n потребителей энергии требуется, чтобы сумма потребляемой энергии превышала сумму оттекаемой. В этом случае минимизируется стоимость транспортировки, при условии, что вся произведенная энергия от поставщиков должна быть потреблена.

Обозначим через Хij количество отпускаемой электроэнергии от источников к потребителям, при этом стоимость передачи мощности между узлами i и j не зависит от направления движения этой мощности, поэтому в рассматриваемой задаче Zij = Zji, в связи с этим нумерации количества источников m и потребителей n присваивается одна нумерация — 1, 2, …, (n+ m).

Целевая функция представляет собой сумму произведений удельных стоимостей на величины передаваемых мощностей от одного транзитного узла другому:

(1).

Для оценки удельных затрат передачи мощности Zij через i-ый транзитный узел рассмотрим простейшую транзитную схему, которая была описана выше. Затраты в рассматриваемой упрощенной сети (рисунок 1) с транзитом мощности через потребителя П2 определяются:

(2).

Как видно из соотношения (2) транзитная мощность, проходящая через узел П2, определяется как X22=П3, то есть величина транзитной мощности передаваемая через П2, равна потребляемой мощности потребителя П3. В соотношение (2) X22 не входит, очевидно, что удельные затраты на передачу транзитной мощности через любой i-ый узел Zij=0.

Рисунок 1 Упрощенная сеть а) оптимальная схема при классической постановке транспортной задачи б) транзитная схема По-видимому, вполне возможно, что эта схема (рисунок 1а) электрической сети будет дороже, чем схема на рисунке 1б с теми же самыми поставщиками и потребителями, мощность в которой передается через потребителя П2 к потребителю П3.

Ограничениями при решении транспортной задачи с транзитом мощности будут балансы мощности во всех узлах, относительно схемы (рисунок 1) для узла П2. Тогда, баланс мощности запишется следующим образом:

X12= В22+ X22.

В общем случае для любого j-го потребителя от всех других узлов, за вычетом транзитной мощности, равна мощности этого потребителя:

(3).

Как следует из выше сказанного такое же соотношение можно записать для i-го источника, то есть сумма мощностей оттекающих от i-го источника к другим узлам, за вычетом транзитной мощности Xij, есть мощность этого источника:

(4).

Из соотношения (3) и (4) следует, что транзитная мощность входит в математическую модель транспортной задачи линейного программирования со знаком «-››. Составим транспортную матрицу для решения задачи транзита мощности, алгоритм которой с учетом отличительных особенностей (3) и (4), присущих этой задаче:

• 1. Присвоение сквозной нумерации всем узлам источников и потребителей — 1, 2, …, (n+m);
• 2. любой i-ый узел может передавать транзитную мощность;
• 3. удельная стоимость транзитной мощности через ii-ый узел Zii=0;
• 4. размерность транспортной матрицы — (n+m) (n+m) и она квадратная;
• 5. в транспортную матрицу транзитные переменные Xii входят в решение задачи со знаком «-››;
• 6. вне зависимости от значений все транзитные переменные считаются базисными.

В качестве примера рассмотрим задачу, которая позволяет найти экстремальные значения целевой функции (1), при ограничениях и соотношениях между переменными (2), (3), (4) в диапазоне переменных, определяемых граничными условиями.

Пример 1: В проектируемой системе энергоснабжения [2] имеется два узла источников электроэнергии и три узла потребителей. Мощность источников И1=50 и И2=30, мощности потребителей соответственно П3=35, П4=25, П5=20 (рисунок 2). Ставится задача рассчитать оптимальную схему сети энергообмена между ее участниками для поставленной задачи, используя транзитную технологию.

Удельные затраты при передаче мощности по линиям, соединяющим узлы источников и потребителей несколько изменятся, а с учетом того, что Zii=0 получаем следующее:

Z12=2,5; Z13=1,4; Z14=1,3; Z15=1,2; Z21=2,5; Z23=1,7; Z24=2,0; Z25=1,5; Z31=1,4; Z32=1,7; Z34=2,0; Z35=2,1; Z41=1,5; Z42=2,0; Z43=2,0; Z45=1,3; Z51=1,2; Z52=1,3; Z53=2,1; Z54=1,3.

Рисунок 2 Проектируемая система энергоснабжения Для данного примера это будет транспортная матрица транзита мощности 5×5, представленная в таблице 1. Улучшенное решение будем искать методом потенциалов, для этого в таблице 1 установлены балансы мощности по строкам и столбцам, согласно методу потенциалов и удельной мощности. Присвоим потенциалы Vi каждой строке и Uj каждому столбцу, которые взаимосвязаны соотношением:

Vi +Uj = Zij.

Таблица 1.

Найдем величины этих потенциалов и поставим их в таблицу 1. Поскольку для базисных переменных (таблица 1).

Zii=0, то Vi =-Uj.

Для улучшения решения проверим возможности перевода свободных переменных в базисные. Для этого рассмотрим свободную переменную Х45, для которой Z45=1,3 является минимальной в пятом столбце. Тогда,.

V4+U5 = -0,6+2,2=1,6.

Следовательно, Х45 можно перевести в базис, строим цикл, начальная вершина цикла лежит в клетке Х45 со знаком «+››, остальные вершины Х25,.

Х23, Х43. При увеличении свободной переменной Х43 входит со знаком минус ее изменение в отрицательную сторону не ограничено, а переменные со знаком плюс ограничены нулем. Таким образом, значение всех переменных в цикле следует изменить на 5 у.е.

Аналогично строим цикл для Х53. В результате получим новое допустимое решение, результаты сведены в таблице 2.

Таблица 2.

Для полученного допустимого решения найдем значение целевой функции, базисные переменные в которой соответственно равны:

Х15=20, Х54=25, Х43=5, Х23=30.

При этом в решении выполнено условие Vi +Uj < Zij, и оно является оптимальным.

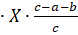
Этому решению соответствует следующая схема (рисунок 3):

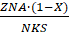
Рисунок 3 Оптимальная транзитная схема электросети Как видно из приведенного решения количество ветвей в этой сети минимальное, что свидетельствует об эффективном снижении затрат на строительство сети, а сам механизм позволяет оптимизировать транспортировку от поставщиков электроэнергии к потребителям.

Таким образом, технологические характеристики и совершенствование эксплуатационного обслуживания способствуют эффективной экономической оптимизации транзитной транспортировки мощностей и, как следствие, повышает конкурентоспособность на энергорынке.

• 1. Аввакумов В. Г. Постановка и решение электроэнергетических задач исследования операций. — Киев: Вища школа, 1983.
• 2. Костин В. Н. Оптимизационные задачи электроэнергетики Учебное пособие СЗ гзту. Издательско-полиграфическая ассоциация вузов Санкт-Петербург, 2003.
• 3. Степанов В. В., Степанова М. В., Степанов В. В. Оптимизация поставки электроэнергии на примере использования транспортной задачи.- Сборник научных статей XVII всероссийская научно-практическая конференция (заочная) «Инновационные технологии в образовательном процессе, Краснодар, 2015
• 4. Степанов В. В., Степанова М. В., Кабанков Ю. А. Применение транспортной задачи для оптимизации в межрегиональных сетевых компаниях передачи электроэнергии.- YI Международная научно-практическая конференция молодых ученых, посвященная 55-й годовщине полета Ю. А. Гагарина в космос», Краснодар, 2016.