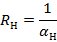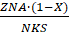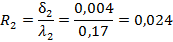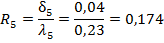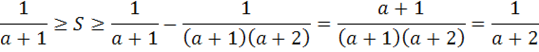Свойства числа е

Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения.

является функция.

.

где c — произвольная константа.

• 1. Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
• 2. Число e является вычислимым (а значит, и арифметическим) числом.

— формула Эйлера, в частности.

5. т. н. «интеграл Пуассона» или «интеграл Гаусса» .

6. предел.

7.

8. Представление Каталана:

9. Представление через произведение:

10. Через числа Белла:

11. Мера иррациональности числа e равна 2 (что есть наименьшее возможное значение для иррациональных чисел).

Доказательство иррациональности

Предположим, что.

.

где a и b — натуральные числа. Учитывая данное равенство и рассматривая разложение в ряд:

получаем следующее равенство:

Представим данную сумму в виде суммы двух слагаемых, одно из которых — сумма членов ряда по n от 0 до a, а второе — сумма всех остальных членов ряда:

Теперь перенесем первую сумму в левую часть равенства:

Умножим обе части полученного равенства на. Получим.

Теперь упростим полученное выражение:

Рассмотрим левую часть полученного равенства. Очевидно, что число целое. Целым является также и число, поскольку (отсюда следует, что все числа вида целые). Тем самым левая часть полученного равенства — целое число.

Перейдем теперь к правой части. Эта сумма имеет вид.

По признаку Лейбница этот ряд сходится, и его сумма S есть вещественным числом, заключенное между первым слагаемым и суммой первых двух слагаемых (со знаками), т. е.

Оба эти числа при лежат между 0 и 1. Следовательно, т. е. — правая часть равенства — не может быть целым числом. Получили противоречие: целое число не может быть равно числу, которое не является целым. Это противоречие доказывает, что число e не является рациональным, а следовательно является иррациональным.