Измерение напряжения и тока

Определить предел абсолютной и относительной погрешности измерения напряжения, если измерения проводились магнитоэлектрическим прибором с классом точности и пределом измерения. Результат измерения В. Вольтметр с нулём в начале шкалы.

Решение.

1. В — нормирующее значение;

Значение абсолютной погрешности будет равно:

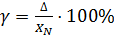
; (3.1).

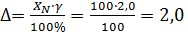
В; (3.2).

Где — приведённая погрешность (класс точность прибора);

— абсолютная погрешность.

2. Значение относительной погрешности будет равно:

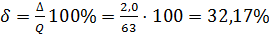
; (3.3).

Ответ: В,. [2].

Задача 2

Оценить инструментальные погрешности измерения тока двумя магнитоэлектрическими амперметрами с классами точности и и указать, какой из результатов получен с большей точностью, а также могут ли показания мА и мА исправных приборов отличаться так, как задано в условии. Приборы имеют нули в начале шкалы и пределы измерения мА и мА.

Решение.

1. Найдём значения абсолютных погрешностей для двух приборов.

мА — нормирующее значение для первого амперметра;

мА — нормирующее значение для второго амперметра;

Значение абсолютной погрешности будет равно:

; (6.1).

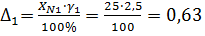
мА; (6.2).

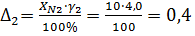
мА; (6.3).

Где — приведённая погрешность (класс точность прибора);

— абсолютная погрешность.

2. Значение относительных погрешностей двух амперметров будет равно:

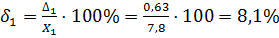
; (6.4).

; (6.5).

Вывод: результат, измеренный с помощью второго амперметра, получен с большей точностью При исправных приборах модуль разницы их показаний не должен превышать суммы модулей абсолютных погрешностей, т. е. должно выполняться условие:

(6.6).

Вычисляем:

;

.

Условие выполняется, следовательно, такие показания могут быть получены при исправных приборах. [2].

Задача 3

Требуется выбрать магнитоэлектрический вольтметр со стандартными пределами измерения и классом точности, при условии, что полученный результат измерения напряжения должен отличаться от истинного значения не более, чем на .

Решение.

• 1. Выберем стандартный предел измерения 100 В из ряда 1, 3, 10, 30…
• 2. Выберем стандартный класс точности. Для этого рассчитаем значение приведённой погрешности:

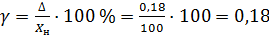
(10.1).

Где — нормирующие значение, принятое равным пределу измерения.

Выберем ближайший класс точности 0,1.

Вывод: был выбран стандартный предел измерения 100 В. Это связано с тем, что измеренное значение должно быть как можно ближе к значению предела измерения, т.к. при его увеличении в большую сторону и неизменном результате измерения повышается относительная погрешность.

Был выбран стандартный класс точности 0,1. Он был выбран меньше значения рассчитанной приведённой погрешности для увеличения точности средства измерения. [2].

Задача 4

В процессе обработки результатов прямых измерений сопротивления определено: среднее арифметическое значение этого напряжения кОм, границы неисключенных остатков трёх составляющих систематической погрешности.

кОм, кОм, кОм.

Требуется определить доверительные границы суммарной погрешности результата измерения и записать его в соответствии МИ 1317−86 или ГОСТ 8.207−76. Значение доверительной вероятности принять.

.

При расчётах полагать, что случайная погрешность пренебрежительно мала, а число наблюдений существенно больше 30.

Решение.

1. Т.к. случайная погрешность пренебрежительно мала, то доверительные границы случайной состовляющей:

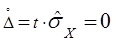
Ом (15.1).

2. Определяем доверительные границы неисключенной систематической погрешности результата измерения.

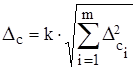
(15.2).

где m — число суммируемых погрешностей;

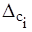
— граница i-й неисключенной систематической погрешности;

k — коэффициент, определяемый принятой доверительной вероятностью.

Коэффициент k определяют по графику зависимости (рисунок 1) k = f (m, l), где m — число суммируемых погрешностей;

;

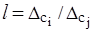
кривая 1 — для m =2; кривая 2 — для m = 3; кривая 3 — для m = 4.

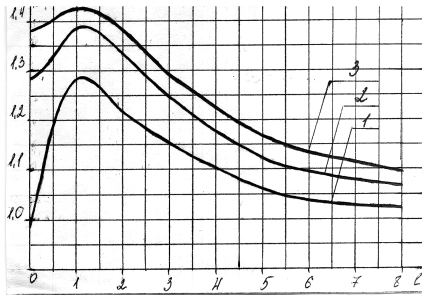
Рисунок 1 — График зависимости k = f (m, l).

Найдем коэффициент k для нашего случая. Выберем наиболее отличную от всех составляющую систематической погрешности и разделим её на ближайшую по величине:

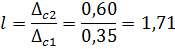
По графику кривой № 2 выбираем коэффициент. Коэффициент k равен 1,35.

Тогда: погрешность магнитоэлектрический прибор

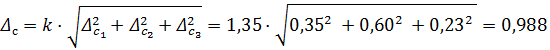
кОм (15.3).

За доверительные границы неисключенной систематической погрешности примем меньшее из и :

3. Т.к. случайная погрешность пренебрежительно мала, то определение границы суммарной погрешности результата измерения нецелесообразно и доверительные границы суммарной погрешности будут равны доверительным границам неисключенной систематической погрешности результата измерения.

(15.4).

4. Записываем результат измерения. Так как погрешность симметрична относительно результата измерения, то.

R = (9,48 0,99) кОм, Рд = 0,99 (15.5).

Ответ: R = (9,48 0,99) кОм, Рд = 0,99. 1].

Задача 5

Напряжение в электрической цепи определялось косвенным методом путём многократных измерений (n=40) напряжений.

B, B и B с последующим расчётом.

.

Оценки средних квадратических отклонений среднего арифметического.

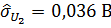
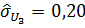
, В,.

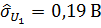
оценка коэффициента корреляции между погрешностями измерений.

, .

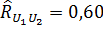
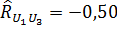
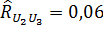
Определить случайную погрешность результата косвенного измерения с доверительной вероятностью Рд = 0,99 и записать результат по одной из установленных форм.

Решение.

1. Находим значение результата косвенного измерения напряжения.

U = U1 + U2 + U3 В (19.1).

2. Определяем частные случайные погрешности косвенного измерения.

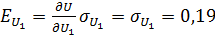
В; (19.2).

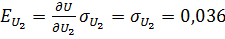
В; (19.3).

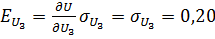
В; (19.4).

3. Вычисляем оценку среднего квадратического отклонения результата косвенного измерения:

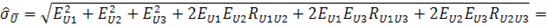
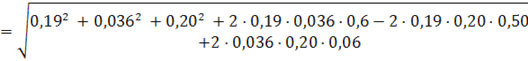
В (19.5).

4. Определяем значение коэффициента Стьюдента t для заданной до-верительной вероятности Рд и числа наблюдений n.

При n > 30 значение t = 2,576.