Примеры. 
Теория вероятностей

1. В партии из 10 изделий 2 бракованных. Наугад выбирают 3 изделия. Определить вероятность того, что среди этих изделий будет хотя бы одно бракованное.

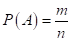
Решение: Требуемую вероятность находим по формуле классического распределения вероятности. Сначала находим n — общее число возможных исходов в данном испытании. поскольку порядок изделий безразличен. 3 изделия из 10 можно выбрать.

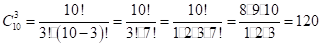
способами.

Теперь найдем число благоприятных исходов m — число исходов, при которых окажется хотя бы 1 бракованное изделие из 3-х выбранных. Поскольку число бракованных изделий в партии равно 2, благоприятными будут исходы, когда из 3-х выбранных изделий будет 1 или 2 бракованных. Найдем число благоприятных исходов m₁, когда среди 3 выбранных изделий оказывается 1 бракованное.

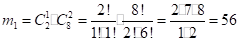
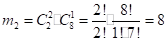
Найдем число благоприятных исходов m₂, когда среди 3 выбранных изделий оказывается 2 бракованных.. Общее число благоприятных исходов. Окончательно:

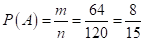
2. Из колоды в 36 карт наугад вынимают 3 карты. Какова вероятность того, что среди них окажется 2 туза. Решение: Требуемую вероятность находим по формуле классического распределения вероятности. Сначала находим n — общее число возможных исходов в данном испытании. Поскольку порядок карт безразличен, 3 изделия из 36 можно выбрать.

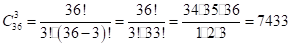
способами.

Теперь найдем число благоприятных исходов m — число исходов, при которых окажется 2 туза из 3-х выбранных карт. 2 туза из 4 можно вынуть способами. Поскольку каждая комбинация из тузов может сочетаться с любой комбинацией из остальных карт, всего получится варианта. Окончательно получаем:

.

3. 12 рабочих получили путевки в 4 дома отдыха: 3 — в первый, 3 — во второй, 2 — в третий и 4 — в четвертый. Найти вероятность Р (А) того, что данные трое рабочих поедут в один дом отдыха.

Решение: Вероятность того, что данные трое рабочих окажутся вместе и попадут в любой из 4-х домов отдыха равна. Поскольку в третий дом отдыха выделено всего 2 путевки, им необходимо попасть в оставшиеся 3 из 4 домов отдыха. Вероятность этого события Р (¾) = 0,75.

Окончательно получаем:

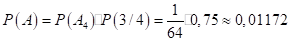
• 4. При изготовлении детали заготовка должна пройти 4 операции. Предполагая появление брака на отдельных операциях событиями независимыми, найти вероятность изготовления стандартной детали, если вероятность появления брака на первой операции равна 0,05, на второй — 0,01, на третьей — 0,02, на четвертой — 0,03.Решение: Вероятность изготовления годной детали Р (А) равна произведению вероятностей изготовления годной детали на каждой операции Р (Аi). Следовательно
• 5. Некоторый механизм состоит из 6 частей, из которых 2 изношены. При работе механизма включаются случайным образом 2 части. Найти вероятность того, что включенными окажутся неизношенные части. Решение: С помощью формулы гипергеометрического распределения определяем искомую вероятность того, что включенными окажутся неизношенные части.

.

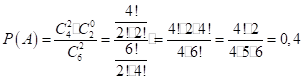
6. Произведен залп из двух орудий по мишени. Вероятность попадания из первого орудия равна 0,85, из второго 0,91. Найти вероятность поражения цели.

Решение: Обозначим вероятность попадания из первого орудия через Р (А), а из второго Р (В). При поражении цели возможны 3 варианта: когда оба орудия попали в цель — вероятность этого события равна.

;

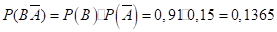
когда в цель попало только первое орудие — вероятность этого события равна; когда в цель попало только второе орудие — вероятность этого события равна. Тогда вероятность поражения цели будет равна сумме всех трех вероятностей:

7. Рабочий обслуживает 4 станка. Вероятность того, что в течении часа первый станок не потребует внимания рабочего, равна 0,7, для второго станка — 0,8, для третьего — 0,9, для четвертого — 0,85. Найти вероятность того, что в течении часа по крайней мере один станок не потребует внимания рабочего.

Решение: Здесь вероятности р₁ = 0,7; р₂ = 0,8; р₃ = 0,9; р₄ = 0,85 есть вероятности того, что один из станков потребует внимания рабочего в течении часа, а q₁ = 0,3; q₂ = 0,2; q₃ = 0,1; q₄ = 0,15 есть вероятности того, что один из станков не потребует внимания рабочего в течении часа. Найдем вероятность противоположного события: вероятность того, что в течении часа все станки потребуют внимания рабочего.

.

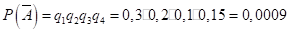
Тогда вероятность того, что в течении часа по крайней мере один станок не потребует внимания рабочего будет равна.

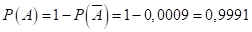
8. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 0,3% брака, второй — 0,2% и третий — 0,4%. Найти вероятность попадания на сборку бракованной детали, если с первого поступило 1000, со второго — 2000 и с третьего — 2500 деталей.

Решение: Решим пример по формуле полной вероятности. В качестве гипотез примем события, заключающиеся в следующем: Н₁ — произвольно выбранная деталь, изготовлена на первом автомате, Н₂ — произвольно выбранная деталь, изготовлена на втором автомате, Н₃ — произвольно выбранная деталь, изготовлена на третьем автомате; событие, А заключается в том, что попавшая на сбору деталь бракованная. По формуле полной вероятности имеем:

где: — вероятность того, что выбранная деталь бракованная, при условии, что она с i-го автомата соответственно; Р (Н_i) — вероятности гипотез. Найдем вероятности гипотез.

Окончательно получаем:

.

9. Имеется 10 одинаковых по виду урн, из которых в 9 находится по 2 черных и 2 белых шара, а в одной — 5 белых и 1 черный шар. Чему равна вероятность того, что шар взят из урны, содержащей 5 белых шаров, если он оказался белым.

Решение: Вероятность Р (А) того, что шар взят из урны содержащей 5 белых шаров, если он оказался белым равна произведению вероятность того, что шар взят из урны, содержащей 5 белых шаров Р (Н) на вероятность того что взятый из этой урны шар оказался белым Р (Б).

Р (Н) = 1/10; с помощью формулы гипергеометрического распределения.

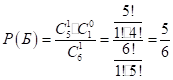
Окончательно получаем: .

10. В магазин вошли 10 покупателей. Вероятность совершить покупку для каждого вошедшего одна и та же и равна 0,2. Найти вероятность того, что 6 из них совершат покупку.

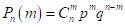
Решение: Применяем формулу Бернулли. Здесь n = 10, m = 6, р = 0,2, q = 1 — 0,2 = 0,8. По формуле Бернулли получаем.

11. Случайная величина имеет распределение вероятностей, представленное таблицей:

Построить многоугольник распределения и найти функцию распределения F (х).

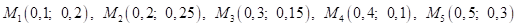
Решение: Возьмем прямоугольную систему координат и по оси абсцисс будем откладывать значения, а по оси ординат вероятности. Возьмем точки и соединим их отрезками прямых. С учетом боковых ординат получим замкнутый многоугольник (рис. 4), который изображает закон распределения данной дискретной случайной величины графически.

Рис. 4.

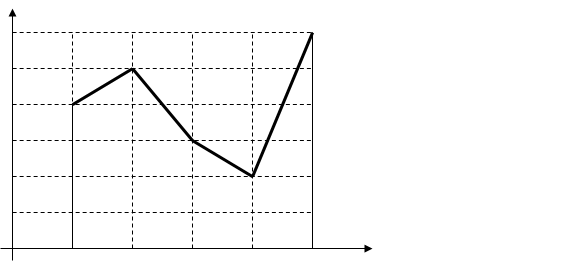
0,1 0,2 0,3 0,4 0,5.

Поскольку случайная величина обязательно принимает одно из 5 значений, которые образуют полную группу попарно несовместимых событий, применяя теорему сложения вероятностей получаем, что сумма их вероятностей равна вероятности достоверного события, т. е. равна 1:

.

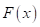
Функция распределения данной случайной величины будет ступенчатой, кусочно-постоянной (рис.5):

Рис. 5.

0,1 0,2 0,3 0,4 0,5.

12. Найти случайной величины о примера 11.

Решение: Найдем требуемые числовые характеристики случайной величины:

13. — непрерывная случайная величина с плотностью распределения (х), заданной следующим образом.

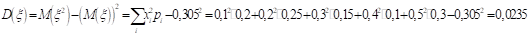
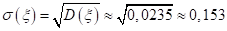
Найти, А и функцию распределения F (х).

Решение: Для нахождения, А воспользуемся свойством плотности распределения:

Следовательно А=3.

Для нахождения функции распределения F (х), связанной с плотностью формулой, будем рассматривать три возможных случая расположения х:

• а) ;
• б) ;
• в) .