Части графа.
Геометрическая теория графов

Ясно, что после применения конечного числа операций разборки этих двух видов получится новый граф Gj (Vj, Ei, //), не изоморфный исходному графу G (V, Е, f). Заметим, что вторую операцию разборки можно заменить композицией конечного числа операций 1 и операции 2*. Легко видеть, что для элементов графа Gi (Vj, Ej, fi) имеют место следующие свойства: Граф GI может быть получен из графа G только при… Читать ещё >
Части графа. Геометрическая теория графов (реферат, курсовая, диплом, контрольная)
Пусть задан некоторый конечный граф G (V, Е, f). В силу следствия из теоремы 2 этот граф всегда можно мыслить как некий геометрический граф, т. е. как совокупность конечного множества точек-вершин пространства, некоторые пары из которых соединены простыми кривыми-ребрами (петлями — если пара состоит из дважды взятой вершины). Существует ряд операций, называемых операциями разборки графа, позволяющих из исходного графа получать новые графы, множества вершин которых являются подмножествами множества V, а множества ребер — подмножествами множества Е. При этих операциях должно сохраняться отношение инцидентности, имеющее место для исходного графа G при выполнении разумного требования о том, что множество вершин графа G/ должно включать все граничные точки множества его ребер. Существует два основных вида операций разборки графа G:
- 1) удаление ребра между двумя вершинами графа G с сохранением граничных вершин;
- 2) удаление вершины графа G вместе со всеми ей инцидентными ребрами.
Частным случаем второй операции разборки является операция.
2 ) удаление изолированной вершины графа G.
Ясно, что после применения конечного числа операций разборки этих двух видов получится новый граф Gj (Vj, Ei, //), не изоморфный исходному графу G (V, Е, f). Заметим, что вторую операцию разборки можно заменить композицией конечного числа операций 1 и операции 2*. Легко видеть, что для элементов графа Gi (Vj, Ej, fi) имеют место следующие свойства:
a) V/cVuE; сЕ;
- б) f/(e)=f (e) для каждого ее Ej;
- в) если ее Ei, uf (e)=(xj & xz), то xj е Vj’u xz e V/.
Граф Gy, полученный из графа G При помощи конечного числа операций разборки, называется частью графа G. Другими словами, частью графа G называется такой граф Gj, для которого выполняются условия а), б), в).
В теории графов представляют интерес два наиболее важных вида частей графа — подграф и су граф.
Подграфом графа G называется такая его часть Gy, которая получается из графа G при помощи конечного числа операций разборки вида 2, т. е. — при помощи удаления конечного числа вершин вместе со всеми примыкающими к ним ребрами. Другими словами, подграф С/ - это такая часть графа G, для которой Яу — все ребра из Е, концы которых лежат в V/. Граф G по отношению к своему подграфу Gy называется надграфом.
Суграфом графа G называется такая его часть Gy, которая получается из графа G при помощи конечного числа операций разборки вида 1, т. е. — при помощи удаления конечного числа ребер (с сохранением вершин). Другими словами, су граф G/ - это такая часть графа G, для которой V/ = V. Граф G по отношению к своему су графу Gy называется сверхграфом.
Граф G по отношению к произвольной своей части G/ называется объемлющим графом.
Пример. Пусть G (V, Е) - это граф автомобильных дорог некоторого государства. Здесь V — множество всех городов этого государства, а Е — совокупность всех дорог между городами. Если удалить из графа G все второстепенные дороги, то получим граф главных дорог государства, который является суграфом графа G. Рассмотрим теперь некоторую губернию этого государства. Удалим из графа G все города, не находящиеся на территории этой губернии, вместе со всеми примыкающими к ним дорогами. В результате получим граф автомобильных дорог этой губернии, являющийся подграфом графа G.
Упражнения
1. Докажите, что графы Gj, G2 и G3 являются частями графа G (см. рис. 19а-19г). Какие из этих графов являются подграфами и какие — суграфами объемлющего графа G. Указать процессы разборки графа G, приводящие к графам G/, G2 и G.?.
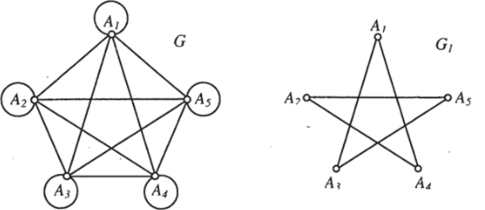
Рис. 196.
Рис. 19а
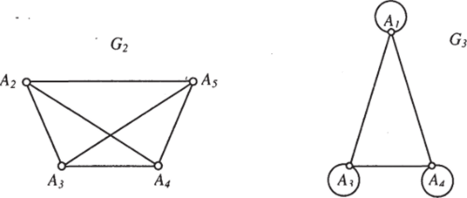
Рис. 19г
Рис. 19в
- 2. Докажите, что при к < п любой полный граф с к вершинами является подграфом полного графа с п вершинами.
- 3. Докажите, что при к < п любой полный граф с петлями, имеющий к вершин, является подграфом полного графа с петлями, имеющего п вершин.
- 4. Докажите, что любой полный граф является суграфом полного графа с петлями, имеющего столько же вершин.
- 5. Докажите, что при к < п любой полный граф, имеющий к вершин, является частью полного графа с петлями, имеющего п вершин.
- 6. Докажите, что частями двудольного графа являются графы, также являющиеся двудольными.
- 7. Докажите, что подграф двудольного полного графа является двудольным полным графом.
- 8. Можно ли при помощи операций разборки из двудольного графа получить Л:-дольный граф (к >2)?
- 9. Докажите, что полный граф является
сверхграфом любого полного двудольного графа с тем же количеством вершин.
10. Докажите, что полный граф является сверхграфом любого к-дольного графа с тем же количеством вершин.
Ответы и пояснения
1. Граф GI может быть получен из графа G только при помощи удаления ребер (т.е. с использованием операции разборки вида 1). Эта операция применяется 10 раз при удалении следующих ребер: Aj & А], А2 & Л2, Аз & Аз, А4 & А4, A3 & A3, А] & А2, А2 Аз, A3 & А4, А4 & Аз и Аз & А/. Следовательно, Gj является суграфом графа G (а, следовательно, — и частью этого графа).
Граф Сг может быть получен из графа G, например, при помощи следующих операций разборки:
- • удаление всех петель. (пятикратное применение операции разборки вида 1);
- • удаление вершины А/, вместе со всеми ей инцидентными ребрами (операция разборки вида 2).
Таким образом, граф G? является частью графа G.
Граф G} может быть получен из графа G при помощи двукратного применения операции разборки вида 2 (удаление вершин Л 2 и As вместе со всеми инцидентными им' ребрами. Следовательно Gj — подграф (и часть) графа G.
Заметим, что G — это полный граф с петлями, содержащий 5 вершин; G/ - граф, изоморфный правильному пятиугольнику; G: — полный граф с 4 вершинами; G} — полный граф с петлями, содержащий 3 вершины.
- 2. Для доказательства достаточно удалить любые (п — к) вершин вместе со всеми инцидентными им ребрами.
- 3. Доказательство проводится в полной аналогии с упражнением 2.
- 4. Если полный граф с петлями имеет п вершин, то после удаления п петель (операция разборки вида 1) получим полный граф с п вершинами.
- 5. Необходимо убрать все петли (операция разборки вида 1) и удалить любые (п — к) вершин вместе со всеми им инцидентными ребрами (операция разборки вида 2).
- 6. Если граф является двудольным, то вершины из одной «доли» не смежны. После применения операций разборки вершины, оставшиеся внутри каждой «доли», снова будут несмежными.
- 7. Применение операции разборки вида 2 не меняет смежности вершин, не участвующих в этой операции.
- 8. Можно. Пусть, например, двудольный граф имеет к вершин. Удалим все ребра у этого графа (операция разборки вида 1). В результате получим нуль-граф с к вершинами, который можно рассматривать как-дольный граф, являющийся суграфом исходного двудольного графа.
- 9. Если вершины полного графа разделить на два подмножества и удалить ребра, соединяющие вершины внутри каждого из этих подмножеств (операция разборки вида 1), то получим полный двудольный граф, для которого исходный граф будет являться сверхграфом. Например, при удалении из полного графа с пятью вершинами четырех ребер, изображенных пунктиром (см. рис. 20), получается полный двудольный граф.

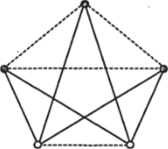
- — Рис 20
- 10. Доказательство аналогично упражнению 9.