Теория множеств в описании сигналов

Рассмотрим способы представления временной функции х (0 в сжатом виде, позволяющие идентифицировать функции и отличать их друг от друга. Хорошо знакомым и привычным способом является графическое изображение функции (график), как совокупность упорядоченных пар значений {t, x (t)}, взятых достаточно плотно и представленных в прямоугольной системе координат При графическом представлении сигналы изображаются сложной совокупностью точек, кривой в простой области — двумерном пространстве. В отличие от этого можно ввести более сложные пространства — пространства сигналов, в которых каждый сигнал изображается простейшим элементом — точкой. С этой точки зрения рассмотрим сигнал как элемент множества S. Само множество определяется некоторым свойством Р, которое справедливо для любого элемента множества. Условно это изображается так: S = {х; Р}, т. е. S есть множество всех х, для которых справедливо Р. Вводя дополнительное обозначение, можно записать Р => х е S, что означает: «Р верно для х, принадлежащего S». Определив свойство Р, мы задаем тем самым множество сигналов.

Гармонические сигналы

Обозначим через S_c множество всех гармонических (синусоидальных) сигналов, т. е.

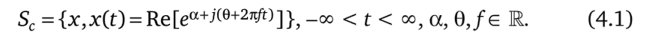
Утверждение ос, 0, /е Шв (4.1) означает, что эти параметры могут произвольно выбираться из множества всех действительных чисел R. Поэтому S_c содержит гармонические колебания со всевозможными амплитудами, фазами и частотами.

Часто свойство Р для конкретного множества можно указать в другой форме, например

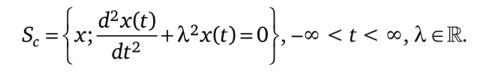
Периодические сигналы

Мы будем обозначать через S_R(T) множество периодических сигналов с периодом Т, т. е.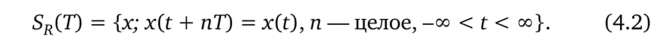

Операции над множествами сигналов

Имея дело с множествами сигналов, полезно применять две элементарные операции теории множеств.

Объединение определяется как.

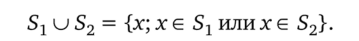
Пересечение определяется как.

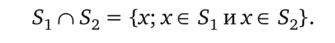
Разбиение и отношение эквивалентности

Операторы и и п могут быть применены для получения разбиения множества на ряд непересекающихся подмножеств. Мы говорим, что совокупность множеств S2, S3, …} образует разбиение множества S, если S = Sj u S₂ u S₃ и … и S₍ п S- = 0 для i ^ j.

При разбиении множества обычно получают более удобные подмножества. Так, можно разбить несчетное множество на конечное или счетное число подмножеств.

Разбиение можно произвести с помощью отношения эквивалентности, и часто это наиболее подходящий способ получения разбиения. Мы говорим, что два элемента эквивалентны, х ~ у, если отношение эквивалентности ~ определено для всех пар элементов и удовлетворяет следующим свойствам:

• а) х ~ х для любого х (рефлексивность);
• б) х ~ у => у ~ х (симметрия);
• в) х ~ у иу ~ z => х ~ z (транзитивность).

Каждое отношение эквивалентности естественным образом порождает разбиение множества на ряд подмножеств S" называемых множествами эквивалентности, причем S_x включает все элементы, эквивалентные х: S_x= {у; у ~ х}, где х — некоторый элемент исходного множества.

Равенство — это отношение эквивалентности, но множества эквивалентности в этом случае содержат только отдельные элементы.

Взяв пример, известный из теории чисел, рассмотрим разбиение множества всех целых чисел {п; п = 0, ±1, ±2, …} на конечное число т множеств эквивалентности:

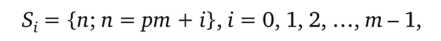
где р — любое число.

Соответствующее отношение эквивалентности п_г ~ п₂ => п₁ — п₂ = = pm =>n_l = п₂ (mod т) называется конгруэнтностью (сравнимостью) по модулю т. Здесь обозначение => может быть прочитано как «порождается». Так, например, разбиение множества всех целых чисел на подмножества, конгруэнтные по модулю 2, приводит к разбиению на четные и нечетные числа.