Приборы на квантово-размерных эффектах

Основой квантовой механики явились экспериментальные факты, согласно которым поток элементарных частиц (например, электронов) проявлял типично волновые свойства, такие как интерференция и дифракция. Это позволило рассматривать поток частиц с импульсами р как некоторую плоскую волну, длина которой А,_дБ (называемая длиной волны де Бройля), как показало подробное исследование этого вопроса, связана с р соотношением.

где h = 6,626−1CH³⁴ Дж-с — постоянная Планка (проще всего убедиться в справедливости соотношения (5.7), приравнивая энергию в квантовом Ё — hv — he/ А,_дБ и в корпускулярном Ё-тс² -рс представлениях). Волновая функция vj/(x, у, z, t) микрочастицы имеет тот физический смысл, что |v|/i|/*|dV есть вероятность обнаружить частицу в объеме dV, т. е. |}/|/" | = ||/²| — плотность вероятностного распределения частицы в данной единице объема пространства. Распределение в пространстве волновой функции |/ должно удовлетворять волновому уравнению, которое по аналогии с известным из курса «Теория поля» для напряженности электрического поля электромагнитной волны Е волновым уравнением V²? + к²Е — 0 будет иметь вид.

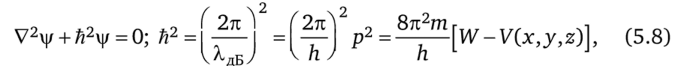
где к — волновой вектор, а импульс р связан с массой частицы т и ее кинетической энергией А — W — V (x, y, z) (где W — полная энергия частицы, V (x, y, z) — потенциальная энергия) очевидным соотношением Л = р²/2т. Уравнение (5.8) записанное в виде.

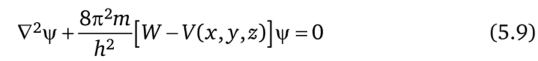
называется уравнением Шредингера. Если частица имеет полную энергию W, то найденная из решения (5.6) с заданными граничными условиями функция |/ должна еще иметь обычный временной множитель.

gj2nvt ₌ gj2nWt/h'

Рассмотрим решение уравнения (5.9) для случая, когда электрон с энергией W встречает на своем пути потенциальный порог (такой порог можно сделать, например, с помощью плоского конденсатора из сеток, между которыми создано тормозящее электроны поле и которые очень близко расположены одна к другой). В дальнейшем будем рассматривать случай, когда W зависит только от одной координаты х, то есть будем рассматривать «одномерные частицы» (рис. 5.38, а), когда V²|/ = d²|//cbc². При этом решение уравнения (5.9) будет в случае У₀ >> W для области х < 0 иметь вид суммы двух волн (падающей и отраженной):

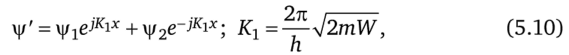
а для х > 0 в виде только падающей слева направо и затухающей волны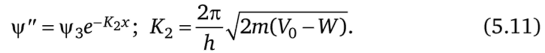

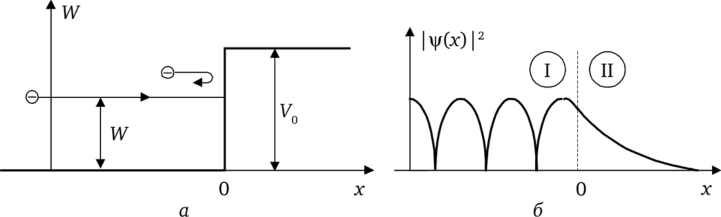
Рис. 5.38. Потенциальный порог для одномерной частицы (а) и плотность вероятности нахождения частицы (б) Из условия равенства функций у' - ц/" прих = 0 (условие отсутствия.

df' du"

разрыва функции) и условия равенства их производных —— = —¹—.

• * *=0 * х=0
• (условие отсутствия излома суммарной функции) нетрудно получить, что

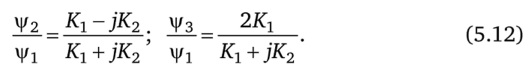
Из чего следует, что коэффициент отражения волны Я = |)/₂/|/₁1² =1, т. е. волна-частица, полностью отражается от потенциального порога при W < V₀, что совпадает с обычными классическими представлениями, причем при х < 0 падающие и отраженные волны образуют стоячую волну (рис. 5.38, б).

Но, в отличие от классических представлений, здесь, согласно выражению (5.11), прих > 0, ||/" |² ~е~^2К2^х, т. е. имеет место частичное проникновение электрона за порог.

Аналогичным образом можно на основе решения уравнения (5.9) рассмотреть с волновых позиций поведение потока электронов, падающих на потенциальный барьер (рис. 5.39, а) или находящихся в потенциальной яме (рис. 5.39, б).

Рассмотрение первого случая показывает, что при этом падающая слева направо волна отразится от барьера не полностью и что имеется определенная вероятность найти электроны за потенциальным барьером, то есть в области III, причем уже из (5.8) легко определить, что если в этой области ц/ = ц/" ', то эта вероятность пропорциональна величине.

где d — ширина барьера. Этот чисто квантовый эффект проникновения частиц сквозь потенциальный барьер при энергии частиц W меньшей высоты V₀ барьера называется туннельным эффектом. Он часто проявляет себя в различных процессах электроники и ядерной физики и находит большое применение в электронике СВЧ.

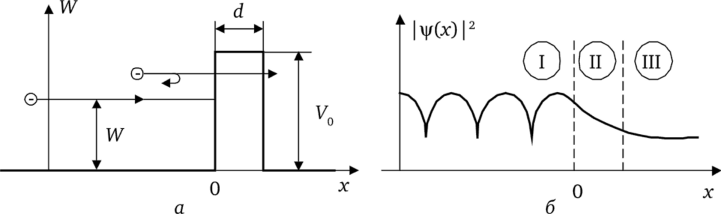
Рис. 5.39. Поток электронов:

а — падающих на потенциальный барьер; б — находящихся в потенциальной яме Решение уравнения (5.9) для случая потенциальной ямы показывает, что частица в яме может иметь лишь строго определенный набор энергий W = W_n, при которых яма шириной а оказывается резонатором для волновой функции 4^/. Этот эффект квантования энергии в потенциальной яме определенных размеров а, близких к величине А,_дБ, называется размерным квантовым эффектом.

В случае бесконечно глубокой потенциальной ямы (рис. 5.40) шириной а решение (5.10) уравнения (5.9) с нулевыми граничными условиями выражается в виде синусоид и показывает, что разрешенные уровни энергии W = W_n в такой яме определяются выражением.

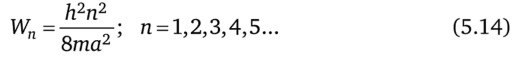
Вид функций Ч' при разных п дан пунктиром на рис. 5.40 и характеризует эффект квантования энергетических уровней.

Если яма будет конечной глубины, то разрешенных уровней в ней будет либо один-два, либо всего лишь несколько штук. Следует отметить, что решение уравнения (5.9) для случая потенциальной ямы, образованной для электронов положительным зарядом (ядром атома), дает серию энергетических уровней W_n, переходы между которыми соответствуют квантам излучения или поглощения, расчетная величина энергии которых hv хорошо совпадает с многочисленными опытами, что в свое время и явилось торжеством и признанием квантовой физики.

Из рис. 5.40 видно, что размер а ямы должен быть по порядку величины близок к Х_дБ, которая для комнатной температуры у электронов в полупроводниках имеет порядок lO⁸ м ~ 10 нм. Современная технология полупроводников позволяет создавать, используя полупроводники с разной шириной запрещенной зоны, слоистые структуры с такой толщиной слоев, т. е. позволяет создавать квантовые ямы и барьеры.

Если рассмотреть структуру с периодически повторяющимися барьерами и ямами, называемую сверхрешеткой, то получим аналог обычного кристалла, в котором потенциальные ямы атомов соединены вместе, что приводит к расплыванию отдельных разрешенных энергетических уровней электронов в атоме в зоны разрешенных значений энергии, между которыми расположены зоны запрещенных значений энергии. Но в отличие от кристалла, в котором атомы расположены достаточно близко и поэтому разрешенные зоны получаются достаточно широкими, в сверхрешетке расстояние между соседними ямами обычно бывает большим и разрешенные зоны на один-два порядка уже, чем в кристалле. Поэтому их называют минизонами (рис. 5.41).

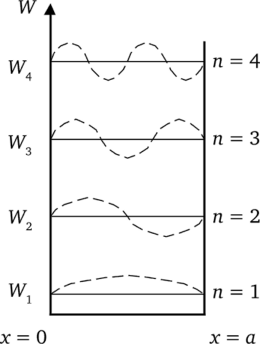
Рис. 5.40. Случай бесконечно глубокой потенциальной ямы (пунктир — функции Ф).

Основным структурным элементом СВЧ-приборов на размерных квантовых эффектах является двойной потенциальный барьер с квантовой ямой посередине, получивший название резонансного туннельного диода (РТД).

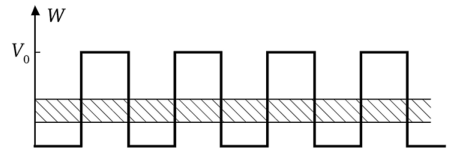
Рис. 5.41. Минизоны сверхрешетки.

Рассмотрим структуру зоны проводимости такого диода (рис. 5.42, а), образованного двумя барьерами широкозонного полупроводника (обычно AlGaAs) и расположенной между ними потенциальной ямой (обычно GaAs), причем по бокам от барьеров пусть имеется высоколегированный (вырожденный) донорный полупроводник (обычно п⁺ GaAs), у которого уровень Ферми W_F лежит ниже первого (нижнего) резонансного уровня W_l потенциальной ямы, а дно зоны проводимости находится на уровне W_Q.

При приложении к такой структуре разности потенциалов U (плюс справа) дно зон проводимости и все уровни двухбарьерной структуры искривляются и опускаются справа вниз (рис. 5.42, б), причем, когда уровень W_F слева расположится против уровня W₁ ямы, появится возможность у электронов левого п⁺-полупроводника туннелировать на резонансный уровень Wj ямы, а оттуда через правый барьер в правый п⁺-полупроводник.

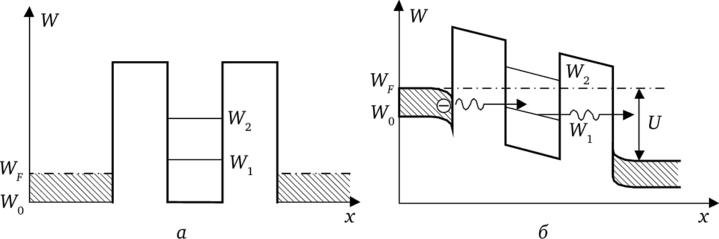
Рис. 5.42. Структура зоны проводимости РТД (а), приложение разности потенциалов U к зоне проводимости (б) При этом через РТД потечет ток, который будет расти с ростом U, а затем уменьшаться практически до тех пор, пока на уровне W_Y ямы не окажется дно зоны проводимости W₀ левого п⁺-полупроводника. После этого, так как слева уже нет электронов, энергия которых удовлетворяла бы условию резонансного туннелирования через яму, ток должен существенно уменьшиться. Но тут начинает проявлять себя эффект обычного туннелирования через два потенциальных барьера (рис. 5.42) и кроме того, практически всегда при этом приближается или даже наступает условие W₂ = W_F резонанса для второго резонансного уровня ямы и ток вновь начинает возрастать с ростом напряжения. Вольт-амперная характеристика РТД при этом имеет вид, показанный на рис. 5.43.

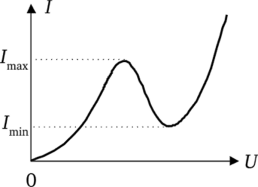
Рис. 5.43. Вольт-амперная характеристика РТД.

Этот вид может существенно изменяться в зависимости от ширины барьеров, ямы и от других конструктивных особенностей РТД. Так, в реальных РТД между барьерами и п⁺-полупроводниками обычно помещаются тонкие нелегированные слои-спаисеры, толщина которых влияет на ход вольт-амперной характеристики (ВАХ) РТД. На рис. 5.44, а показана типичная структура РТД, а на рис. 5.44, б дана зависимость отношения максимального тока ее ВАХ к минимальному от толщины b спайсеров включения и использования, в частности, «паразитных» элементов самого РТД.

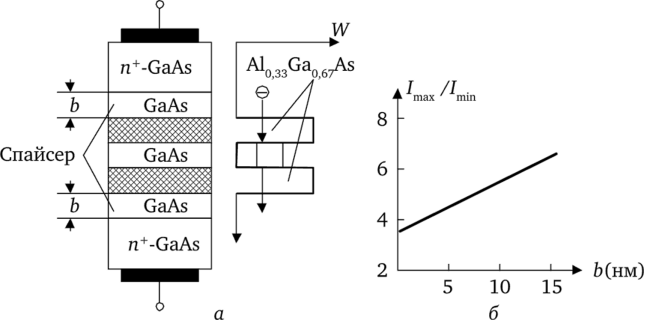
Рис. 5.44. Структура РТД (а), зависимость lmax/lmin (b) (6).

На рис. 5.45 показана простейшая эквивалентная схема автогенератора СВЧ на РТД, причем между точками, а и б дана эквивалентная схема самого РТД, где (-G) — отрицательная проводимость, появляющаяся на падающем участке ВАХ; C_g — емкость шунтирующая (-G) и определяемая участком между n⁺-GaAs; r_s и L_s — сопротивление и индуктивность подводящих участков (п⁺) РТД (C_g; r_s и L_s — «паразитные» элементы РТД; R_H и L_H — параметры нагрузки).

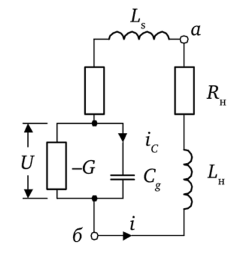
Рис. 5.45. Простейшая эквивалентная схема автогенератора СВЧ на РТД.

Инерционность процесса туннелирования, т. е. время туннелирования, принято оценивать с помощью известного из курса физики соотношения неопределенностей, согласно которому это время т связано с шириной линии резонанса туннелирования AW (как бы «толщиной» каждого их уровней W_1? W₂ и т. д.) соотношением x"h/n (AW), где.

h — постоянная Планка. Такая оценка показывает, что верхняя частотная граница РТД/_верх ~ 1/т > 10¹² Гц = 1 ТГц. Однако в действительности инерционность устройств на основе РТД определяется инерционностью элементов его схемы, при этом максимальная частота генерации автогенератора на РТД равна /_тах -l/4nr_sC_g, т. е. определяется произведением r_sC_g. По ряду оценок эта частота в настоящее время достигла 200 ГГц.

Двухбарьерная структура РТД нашла применение в качестве составной части обычных биполярных и полевых транзисторов (БТ и ПТ) и транзисторов на горячих электронах. Эта структура помещается либо в эмиттер, либо в базу БТ или либо в затвор, либо в исток ПТ. Это создает в выходных характеристиках БТ и ПТ соответствующие участки с уменьшением тока при росте напряжения, что существенно расширяет функциональные возможности БТ и ПТ.

Весьма интересны и перспективны структуры, содержащие последовательное соединение нескольких РТД, в частности, сверхрешетки. Такие структуры имеют ВАХ, содержащую несколько падающих участков тока вдоль оси напряжений, и могут найти широкое применение как в качестве умножителей частоты в большое число раз, так и для построения ряда логических элементов. Такие структуры также включаются в состав БТ и ПТ с целью расширения их функциональных возможностей.