Статистические методы обработки данных

Математические законы теории вероятностей не являются беспредметными абстракциями, лишенными физического содержания, а представляют собой математическое выражение реальных закономерностей, существующих в массовых случайных явлениях [23]. Теория вероятностей дает возможность определить вероятности событий, законы распределения и числовые характеристики случайных величин, но для того, чтобы провести обработку и представить данные, необходимо провести эксперимент, применить (разработать) метод фиксации данных.

Раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений с целью выявления статистических закономерностей, получил название математическая статистика (рис. 11).

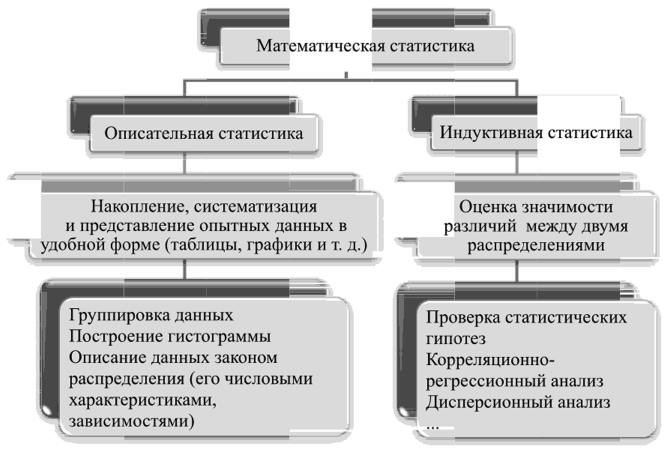
Рис. 11. Направления математической статистики

В связи с этим основной задачей, решаемой математической статистикой, является [23] определение закона распределения случайной величины и нахождение числовых характеристик распределения либо вида функции отклика и ее параметров.

Методы математической статистики используются при планировании организации производства, анализе технологических процессов, для контроля качества продукции и многих других целей.

Определение закона распределения случайной величины

Для определения закона распределения, описывающего заданную выборку (набор экспериментальных данных), необходимо сравнить две выборки данных: экспериментальную и теоретическую, для чего требуется выполнить следующие шаги.

1. Группировка данных и построение гистограммы Для построения гистограммы данные группируют, для чего диапазон изменения значений выборки разбивают на несколько равных интервалов к шириной.

Таблица 6.

Рекомендации по выбору количества интервалов

где х_тт и jc_max — соответственно минимальное и максимальное значения в выборке {*!,…, x_N}. Количество интервалов к согласно различным рекомендациям [24] может получиться разным, а при больших объемах выборок п достаточно большим.

Можно воспользоваться рекомендациями Всероссийского научно-исследовательского института метрологии (табл. 6) [24, 25].

Далее, для каждого интервала подсчитывается количество попадающих в него значений т. Затем для каждого интервала вычисляется относительная частота (3).

По полученным данным строится гистограмма (см. рис. 3).

2. Проведение анализа формы гистограммы и выдвижение гипотезы о законе распределения физической величины Во многих случаях при изучении статистических данных (выборки) необходимо знать закон распределения генеральной совокупности. Для этого проводится сравнение формы гистограммы с внешним видом закономерностей законов распределения. Делается предположение о законе изменения физической величины, т. е. выдвигается статистическая гипотеза о том, что генеральная совокупность распределена по выбранному закону. Данная гипотеза является основной (нулевой) гипотезой Н₀.

Одновременно с основной гипотезой //₀ выдвигается альтернативная гипотеза Н, являющаяся логическим отрицанием гипотезы Я₀ и принимаемая при отвержении гипотезы Н₀.

После выдвижения гипотезы вычисляются значения функции распределения (плотности вероятности и т. д.) для экспериментальной выборки в ряде точек по принятому закону.

3. Проверка правдоподобия гипотезы о законе распределения Проверка статистической гипотезы означает проверку согласования исходных выборочных данных (выборки) с выдвинутой основной гипотезой.

При этом возможны две ситуации — основная гипотеза:

• • подтверждается;
• • опровергается.

Таким образом, при проверке статистических гипотез существует вероятность допустить две ошибки: или, соответственно:

• • опровергнуть верную гипотезу — ошибка первого рода а;
• • принять ложную гипотезу — ошибка второго рода (3.

Вероятность совершения ошибки первого рода называется уровнем значимости. Чаще принимаются уровни значимости а= 0,05; 0,01; 0,001, которые называют пятипроцентным, однопроцентным и 0,1%-м [26].

При проверке гипотезы возможны четыре варианта исходов (табл. 7).

Таблица 7.

Варианты исходов

Для проверки гипотезы Н₀ используют специально подобранную случайную величину — статистический критерий.

Различают следующие статистические критерии:

• • значимости,
• • согласия,
• • проверки на однородность.

Проверка гипотезы на значимость предполагает проверку гипотезы о равенстве численных значений принятого закона распределения двух выборок из генеральных совокупностей случайных величин X и Y.

Проверка на однородность — это проверка гипотезы о том, что две (или более) выборки взяты из одной генеральной совокупности.

Проверка на согласие — проверка предположения о том, что исследуемая случайная величина подчиняется принятому закону распределения.

Существует несколько критериев сравнения законов распределения выборок, так называемых критериев согласия, в частности критерий у (Пирсона), Колмогорова, Смирнова и др.

Выбирается критерий для сравнения законов, вычисляется его значение и сравнивается с его критическим значением. Если значение критерия превосходит критическое, то изменение данных в выборке не соответствует принятому закону. Критические значения для каждого критерия проще всего определять по таблицам.

Критерий Пирсона является универсальным, т. к. применим для любых видов функции F (x), даже при неизвестных значениях их параметров, что имеет место при анализе результатов механических испытаний. Значение критерия Пирсона для выборки определяется как:

где п — объем выборки; к — количество интервалов; m_i — количество значений физической величины X, попавших в тот или иной интервал (абсолютная частота); W_i — относительная частота; p_i0 — теоретическое значение вероятности, вычисленное по формулам принятого закона распределения.

При п—>оо (W; —>?/?,):

р₍ — значение вероятности, определенное по эмпирическим данным.

Пример

Определить возможность описания данных выборки п — 50 определенным законом распределения случайной физической величины при доверительной вероятности 95%. Данные выборки: 19,70; 18,72; 20,24; 21,28; 21,20; 21,73; 17,82; 19,77; 21,10; 18,91; 19,31; 20,31; 18,15; 19,02;

• 19,23; 21,08; 19,43; 20,60; 20,13; 20,23; 20,17; 19,63; 20,34; 19,91; 19,81;
• 19,49; 21,97; 20,87; 22,38; 19,35; 20,66; 21,83; 20,54; 20,90; 19,92; 19,92;
• 20,18; 20,68; 19,62; 20,76; 18,56; 19,15; 18,48; 19,64; 19,97; 20,03; 19,68;
• 20,49; 20,66; 19,26.

Решение

• 1. Определяем минимальное и максимальное значения выборки: %nin ⁼ 17,82, х_тах =22,38.
• 1

Таблица 7.

Параметры выборки

Принимаем количество интервалов к = 8 (см. табл. 6) и определяем ширину интервала (50).

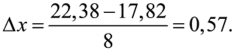
Определим диапазон каждого интервала, абсолютную и относительную частоты (табл. 7).

По данным в таблице строим гистограмму (рис. 12).

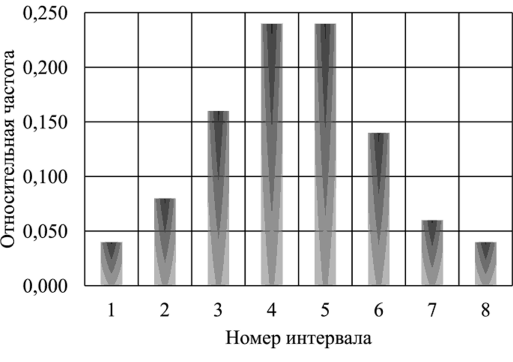
Рис. 12. Гистограмма распределения

которому (29), (30) изменение физической величины зависит от двух параметров: математического ожидания Л/(х) и среднеквадратического отклонения а (х).

Определим математическое ожидание и среднеквадратичное отклонение.

Данные параметры можно определить, воспользовавшись формулами (9), (11) и (13), сделав допущение о том, что Щ —> p_t, а х₍ «х) для интервала:

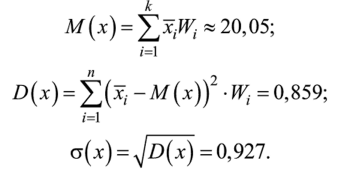
По формуле (38) и табличным данным (прил. 1) определяем расчетные значения вероятности попадания значений физической величины в каждый интервал:

Рассчитав погрешность (2), можно сделать вывод о близости статистического распределения к нормальному закону (табл. 8).

Таблица 8.

Сравнение расчетных и эмпирических вероятностей

Справедливость выдвинутого предположения проверим с помощью критерия согласия Пирсона.

3. Проверка правдоподобия гипотезы Для проверки гипотезы рассчитаем эмпирическое значение коэффициента Пирсона (51)

Для определения критического значения коэффициента Пирсона (прил. 2) найдем число степеней свободы df[21.

где к — количество интервалов выборки (количество варьируемых параметров); г — число параметров предполагаемого распределения, которые оценены по данным выборки:

• • г = 2 — для нормального закона распределения (математическое ожидание и среднеквадратичное отклонение), dfк- 3;
• • г = 1 — для показательного закона распределения (параметр распределения X), df = к- 2. Исходя из числа степеней свободы df = 5, по табличным данным (прил. 2) определяем критическое значение критерия Пирсона:

Так как xl < Хкр> ^то гипотезу о 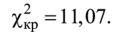нормальном распределении данных в выборке можно принять.