Генерация второй гармоники пучка Гаусса

Лазерные системы — важная прикладная область в современной электронике. Есть несколько способов генерации лазерного луча, но все они имеют одну общую черту: длина волны определяется вынужденным излучением, которое зависит от параметров материала. Особенно трудно найти лазеры, которые производят волны короткой длины (например, ультрафиолетовый свет). С нелинейными материалами возможно сделать гармонику, которая равна кратным числам частоты лазерного света. Из материалов можно непосредственно генерировать лазерный луч с длинной волны равной половине начальной длины.

Эта модель показывает, как создать генерации второй гармоники в моделировании переходных волн, используя нелинейные свойства материала. YAG (л = 1.06 мкм) лазерный луч фокусируется на нелинейный кристалл, таким образом, что наименьшая ширина пучка находится внутри кристалла.

Когда лазерный луч распространяется он проходит в качестве приближенной плоской волны с интенсивностью поперечного сечения гауссовой формы. Ширина пучка определяется как характерная длина гауссовой функции. Сфокусированный лазерный пучок имеет минимальную ширину, в определенной точке вдоль направления распространения. Решение нестационарных уравнений Максвелла дает следующее электрическое поле (X-компонент) [3] (рис. 1):

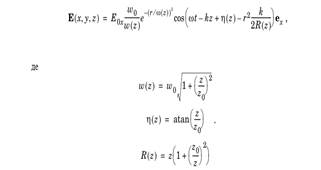
Рис. 1. Уравнение электрического поля (X-компонент).

В этих выражениях:

щ — угловая частота,.

r — радиальная цилиндрическая координата, и k — число волны.

Фронт волны луча не точно плоский, он распространяется, как сферическая волна с радиусом R (z). Близко к точке минимальной ширины волна практически плоская. Эти выражения используются для возбуждения плоской волны на одном конце цилиндра.

В этом примере проблема решена как 2D сечение, которое напоминает осевую симметрию задачи. Тем не менее, через х-поляризацию E-поля, правда, осевая симметрия не может быть использована (доступна в качестве режима приложений в COMSOL Multiphysics [1]). Здесь 9 направлений приближенно со стандартным 2D приятным, пренебрегая оборотом вокруг оси. Вторая гармоника, вероятно, не оказывает существенного влияния на изображение.

Нелинейные свойства для 2-й генерации гармоник в материале можно определить с помощью следующей матрицы,.

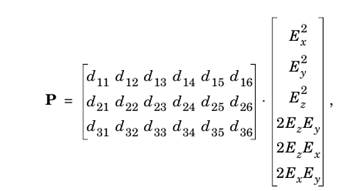
Рис. 3. Матрица поляризации.

где P — поляризация. Модель только использует d11 параметр для простоты. Чтобы сохранять проблемный размер маленьким, нелинейный параметр увеличен некоторыми порядками величины. У кристалла здесь есть F / V, когда ценности для большей части материалы обычно находятся в F / V.

Без этого усиления, найденная 2-я гармоника требует, чтобы z направление геометрии было намного длиннее, приведя к большой проблеме. Гауссов пучок также возбуждается в виде импульса во времени, используя функцию Гаусса конверта.

Основная цель этого моделирования является расчет генерации второй гармоники при импульсе, проходящей по геометрии 20 мкм. Таким образом, мы должны найти то время, которое нужно для импульса, чтобы войти, пройти и исчезнуть с данного объема.

Результаты Импульс имеет характерное время 10 фс, а ниже вы можете увидеть импульс после 60фс.

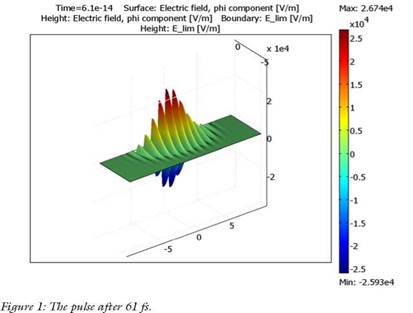
Рис. 4. Импульс после 60 фс.

После 90 фс импульс достигает предела продукции (см. Рис 2). Моделирование должно продолжиться в течение еще 30 фс, таким образом, импульс полностью исчезает.

генерация вторая гармоника пучок гаусс То есть время, при котором импульс пройдет по геометрии 20 мкм = 120 фс.

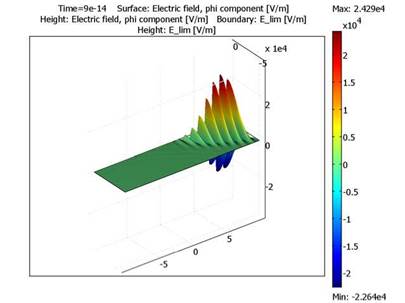
Рис. 5. Импульс после 90 фс.

Библиографический список.

• 1. comSOL Multiphysics [Электронный ресурс]: URL: https: // www.comsol.ru/
• 2. Генерация второй гармоники [Электронный ресурс]: URL: https: // ru. wikipedia.org/wiki/Генерация_второй_оптической_гармоники.
• 3. Гауссов пучок [Электронный ресурс]: URL: https: // ru. wikipedia.org/wiki/ Гауссов_пучок.