Аналитическое конструирование регуляторов с помощью классического вариационного исчисления

Аналитическое конструирование регуляторов (АКР) рассмотрим на следующем примере.

Требуется найти оптимальную передаточную функцию W_f)^p) ре.

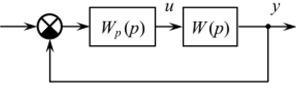
Рис. 1.39. К постановке задачи АКР

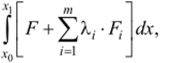
гулятора, который в замкнутой системе с объектом (рис. 1.39), имеющим передаточную функцию.

W[p) = —!— и, соответственно, р+1.

уравнение для переходных составляющих у и и

обеспечивает минимум интеграла 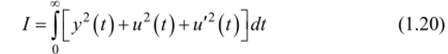при граничных условиях.

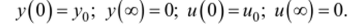
Для вариационной задачи минимизации функционала (1.20) дифференциальное уравнение (1.19) является уравнением связи и может быть записано в виде.

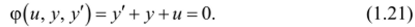
Образуем функцию F*:

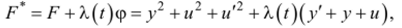
где X (t) — неопределенный множитель Лагранжа.

Поскольку для синтеза регулятора важно знать оптимальные процессы на его входе и выходе, составим уравнения Эйлера относительно переменных y[t) и u (t) для функции F :

Дополняя эту систему уравнением связи (1.21) (уравнение объекта), получим систему уравнений вариационной задачи, переменные которой расположим в соответствующим порядке: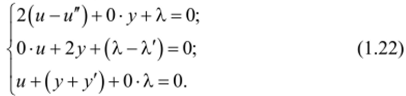

Для решения системы дифференциальных уравнений (1.22) необходимо найти характеристическое уравнение, получаемое путем приравнивания характеристического определителя нулю, т. е.

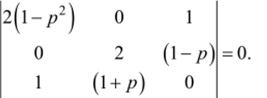
Раскроем определитель, тогда

Характеристическое уравнение (1.23) имеет четыре корня, соответствующих различным сочетаниям знаков «плюс» и «минус» в следующем выражении:

Расположение корней уравнения в комплексной плоскости представлено на рис. 1.40.

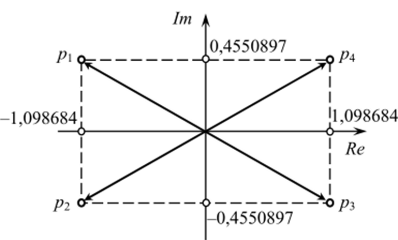
Рис. 1.40. Расположение корней уравнения (1.23) в комплексной плоскости

Для простых корней характеристического уравнения общим решением системы будет сумма экспонент. Например, для рассогласования можно записать:

Постоянные Cj могут быть найдены из граничных условий. Так как по условию задачи j>(oo) = 0, Re (p$) = Re (p) > 0, то отсюда следует, что необходимо принять с₃ =с₄ = 0.

С учетом этого равенства выражение (1.25) примет вид.

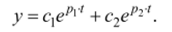
Дифференцируя у и подставляя у в уравнение объекта (1.19), можно найти и. При дифференцировании также можно найти и. Запишем совместно выражения для процессов в системе и их производных:

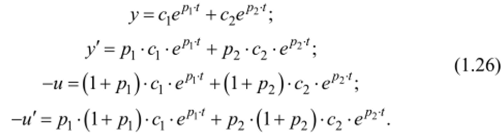
Проанализируем полученное решение. Во-первых, процессы в оптимальной системе соответствуют линейным дифференциальным уравнениям. Отсюда с учетом линейности объекта можно заключить, что оптимальный регулятор также должен быть линейным. Во-вторых, полученное решение соответствует уравнению системы второго порядка.

Так как объект описывается уравнением апериодического звена, то получение уравнения второго порядка для системы требует, чтобы передаточная функция регулятора имела знаменатель первого порядка. Числитель при этом может иметь любой порядок от 0 до 1.

Предположим, что регулятор описывается уравнением.

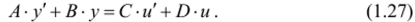
Подставим в (1.27) выражения (1.26) для всех координат и произведем простейшие преобразования. Получим:

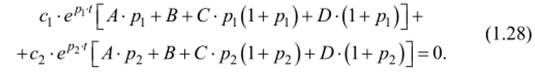
Функции с, •e^Pl‘^t и с₂ •е^Р2‘* не могут быть одновременно тождественно равны нулю, в противном случае у = 0, а это значило бы невыполнение задачи управления. Отсюда следует, что должны равняться нулю обе квадратные скобки в (1.28), т. с.

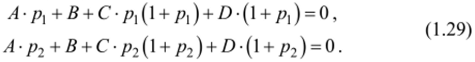
Полученная система уравнений позволяет найти параметры оптимального регулятора, т. е. параметры оптимального закона уравнения.

Поскольку уравнений только два, а неизвестных четыре, то для двух неизвестных могут быть приняты любые значения. Отсюда очевидна неоднозначность получаемого решения. Важно подчеркнуть, что неоднозначность имеется только в выборе параметров (а отсюда и структуры), но оптимальный процесс единственный и определяется системой (1.26).

Рассмотрим некоторые важные решения, вытекающие из (1.29). Проще всего задать пару неизвестных равными нулю. При этом получаем следующие структуры регуляторов:

1) А = С = 0 или В = D = 0 — пропорциональный регулятор с уравнением.

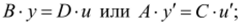
2) В = С = 0 — идеальный дифференцирующий регулятор с уравнением.

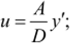
3) А = D = 0 — интегрирующий регулятор (И-регулятор) с уравнением.

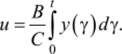
(Сочетания А = С = 0, или С = D = 0, лишены здравого смысла).

Заметим, что при задании любой пары неизвестных нулями и остальные неизвестные при решении системы (1.29) обращаются в нули. Это говорит о том, что рассмотренные структуры регуляторов 1…3 не могут быть взяты в качестве оптимальных.

Рассмотрим еще два сочетания произвольно задаваемых неизвестных:

1. А = О, D = 1. При таком выборе параметров получим регулятор с уравнением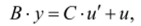

передаточная функция которого имеет вид.

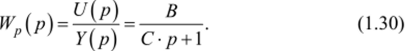
Из (1.30) видно, что полученный регулятор описывается уравнением инерционного звена. Очевидный недостаток этого регулятора заключается в том, что получаемая при этом система является статической.

2. Если задать С = 1 и D = 0, то получим регулятор с уравнением.

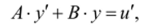
передаточная функция которого.

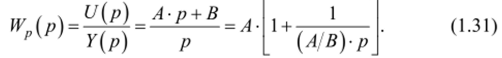
Регулятор с такой передаточной функцией называют пропорционально-интегральным (ПИ-регулятор), причем параметр А трактуется как коэффициент передачи, А/В — как время изодрома. Система с таким регулятором является уже астатической. Поэтому целесообразно в качестве оптимального принять регулятор с передаточной функцией (1.31).

Определим параметры А и В, подставляя в систему (1.29) С = 1 и D = 0:

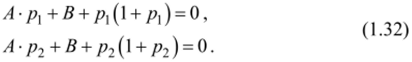
Из (1.32) с учетом числовых значений р, и р₂ (рис. 1.38 или (1.24)) находим:

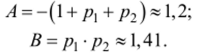
Полученный результат по аналитическому конструированию оптимального регулятора для инерционного объекта имеет большое прикладное значение. Из решения вариационной задачи с функционалом общего вида:

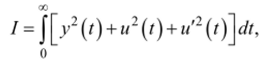
учитывающим качество процессов (слагаемое у² под знаком интеграла), стоимость управления (слагаемое и), возможность технической реализации (^и'² установлено, что оптимальным регулятором является ПИ-регулятор, и найдены его параметры. Этот результат является теоретическим обоснованием широкого применения в промышленной автоматике именно ПИ-регуляторов при управлении инерционными объектами.

Задачи на экстремум при наличии ограничений на допустимые функции сравнений представляют наибольший практический интерес. Так как на практике приходится чаще всего встречаться именно с этой задачей, поскольку в реальных устройствах, системах мы должны считаться с ограниченностью усилий, мощностей, конечных размеров и т. д.

С математической точки зрения это означает, что допускаемые для сравнения функции должны удовлетворять некоторой системе неравенств:

Рассмотрим простейшую задачу. Найти экстремум функционала при условии

Равенство у = cp (jc) определяет границу допустимой области, внутри которой только и может находиться функция, доставляющая экстремум.

Ограниченную область, включающую и свою границу, называют замкнутой областью. При наличии ограничений приходится искать экстремум в замкнутой области.

Основное необходимое условие экстремума — уравнение Эйлера — выводилось прежде в предположении свободы варьирования функций. Или, что-то же самое, предполагалось, что если у (х) удовлетворяет уравнению Эйлера, т. е. является экстремалью, то jK + $y, где 6у>0 и у-Ьу — также являются допустимыми функциями и возможно сравнивать значение функционала на функции W*) и значения функционала на функциях у + 8у и у-8у.

На основании такого сравнения и было выведено уравнение Эйлера. Для замкнутой области такое сравнение нс всегда возможно. Так, если >'(*) проходит по границе, то функция у-8у_у где 5у>0, уже выходит за границы допустимой области. Следовательно, если допустимая область является замкнутой, вывод уравнения Эйлера теряет силу. Экстремум может достигаться и не на экстремалях.

Для того чтобы обойти эту трудность, произведем замену переменных согласно уравнению z² = ^(лег) — ср (лг).

т. е.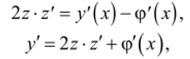

и функционал в новых переменных принимает вид.

На новую переменную z (at) уже не наложено никаких ограничений, границе области соответствует просто значение z = 0.

Экстремум функционала в новых переменных можно искать уже обычным методом, справедливым для открытой области, т. е. искомая функция z (x) должна удовлетворять уравнению Эйлера.

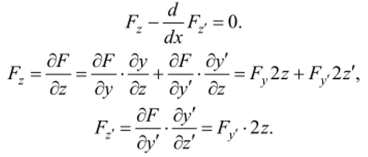
Но Следовательно,.

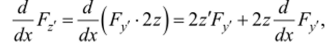
т. e. окончательно.

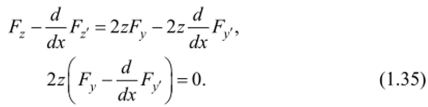
или Это уравнение фактически распадается на два уравнения: z = 0, которому удовлетворяет функция ^ = (р (лг), т. е. граница допустимой области, и уравнение Эйлера для исходного функционала.

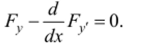
Теперь можно сформулировать окончательный результат. Экстремум функционала (1.33) при наличии ограничений (1.34) может достигаться лишь на кривых, представляющих собой соединение отрезков экстремалей и отрезков границы допустимой области. В частных случаях длина отрезков экстремалей или отрезков границы допустимой области может обращаться в нуль.

К сожалению, уравнение (1.35) указывает лишь на допустимость использования в качестве экстремалей граничных значений функции >> = ф (;с), но нс позволяет доказать, что для линейной задачи, например при ограничении |_у (х)|<1, _y (, v) принимает только граничные значения. Такие доказательства можно получить с помощью принципа максимума, который будет рассмотрен ниже.