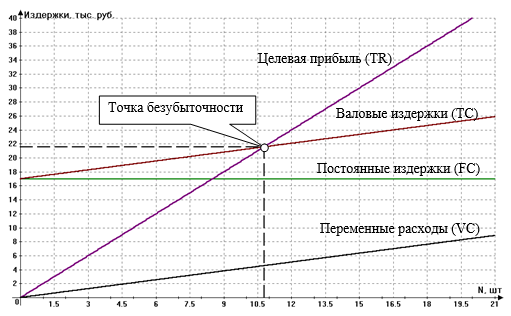
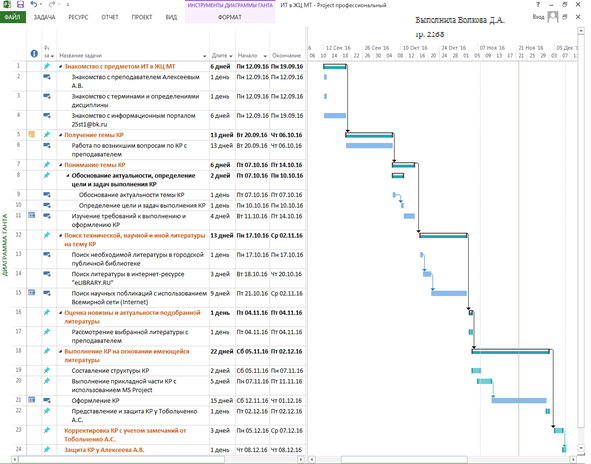
Лекция 2. Основные понятия теории оптимизации

Классификация оптимизационных задач по виду критерия оптимальности

1. Задачи математического программирования.

.

где — скалярная функция на конечномерном множестве :

• — задачи линейного программирования (ЛП): — линейная, допустимое множество Х — выпукло, задается линейными уравнениями и неравенствами. (Ядро ЛП — сиплекс-метод; теория двойственности, функция Лагранжа, существование седловой точки)
• — задачи целочисленного ЛП (оптимальные решения Z);
• — задачи квадратичного программирования;
• — задачи дискретного программирования (допустимое множество — конечно);
• — задачи выпуклого программирования (Х — выпукло, — выпуклая; теорема Куна-Таккера — аналог теории двойственности в ЛП);
• — задачи невыпуклого программирования.
• 2. Задачи многокритериальной оптимизации (критерий оптимальности состоит из нескольких скалярных функций, которые нужно максимизировать или минимизировать).
• 3. Задачи вариационного исчисления.

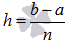
Задача ВИ: найти, Х — произвольное множество, например, , — функционал, аргументом которого чаще всего являются функции (т.е. — подмножество функционального пространства). Для ВИ характерно то, что множество Х — чаще всего является пространством непрерывно дифференцируемых функций.

4. Задачи оптимального управления.

Классический пример задачи ОУ — задача о полете ракеты.

Процесс движения ракеты задается дифференциальным уравнением, начальными условиями, .

Для задачи ОУ характерны разные типы переменных: фазовые (положение в пространстве) и параметры управления (- множество допустимых управлений, которое обычно является множеством кусочно-непрерывных функций).

Кроме того, обычно, .

Требуется так выбрать управление, чтобы минимизировать определенный функционал (расход топлива) минимизировать, при этом попасть в определенную точку пространства.

Постановка классической задачи оптимизации.

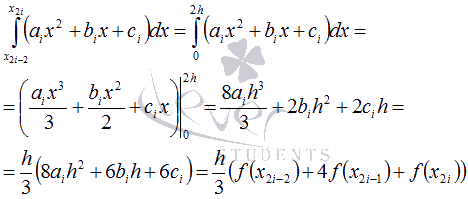
— целевая функция, значение которой характеризуют степень достижения цели (во имя которой поставлена или решается задача);

Х — множество допустимых решений, среди элементов которого осуществляется поиск; - n-мерное евклидово пространство.

Определение 1. Точка называется точкой локального минимума [максимума] функции на множестве Х, если существует окрестность точки такая, что справедливо .

Иначе говоря, условный максимум (минимум) в точке — это наибольшее (наименьшее) значение функции по отношению не ко всем точкам из некоторой окрестности точки, а только к тем из них, которые принадлежат множеству X.

Следует заметить, что сама функция может не иметь экстремума, но иметь условный экстремум.

Определение 2. Точка называется точкой глобального (абсолютного) минимума [максимума] функции на множестве Х, если функция достигает в этой точке своего наименьшего [наибольшего] значения, т. е. .

Замечания.

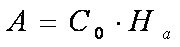
• 1) Задача сводится к задаче поиска минимума следующим образом: .
• 2) Если, то задача (1) называется задача безусловной оптимизации. Если Х задается условиями (ограничениями), накладываемыми на x, то задача (1) называется задачей условной оптимизации.
• 3) Обозначим — множество точек глобального минимума функции на множестве Х.

Тогда решить задачу (1) означает:

— найти множество и значение целевой функции в точках этого множества ;

• — если, то найти ;
• — убедиться, что функция не ограничена снизу на Х;
• — убедиться в том, что .

Определение 1. Градиентом непрерывно дифференцируемой функции в точке x называется столбец-вектор, элементами которого являются частные производные первого порядка, вычисленные в данной точке:

Определение 2. Матрицей Гессе дважды непрерывно дифференцируемой в точке x функции называется матрица частных производных второго порядка, вычисленных в данной точке:

.

где .

Матрица Гессе является симметрической матрицей размера .

Градиент функции направлен по нормали к поверхности уровня (т.е. перпендикулярно к касательной плоскости, проведенной в точке х) в сторону наибольшего возрастания функции в данной точке.

Вектор антиградиента — вектор, равный по модулю вектору градиента, но противоположный по направлению.

Вектор антиградиента указывает направление наибольшего убывания функции в данной точке.

С помощью градиента и матрицы Гессе, используя разложение по формуле Тейлора, приращение функции в точке x может быть записано в виде:

.

.

— евклидова норма вектора.

.

— сумма всех слагаемых разложения, имеющих порядок выше второго относительно приращения аргумента.

Выражение называется квадратичной формой от переменных .

Следовательно, в стационарной точке (в которой градиент функции равен нулю) знак приращения функции, совпадает со знаком выражения .

Определение 3. Квадратичная форма (а также соответствующая матрица Гессе) называется:

положительно определенной (>0), если для любого ненулевого выполняется неравенство ;

отрицательно определенной (), если для любого ненулевого выполняется неравенство ;

положительно полуопределенной (), если для любого выполняется неравенство 0 и имеется отличный от нуля вектор, для которого =0;

отрицательно полуопределенной (), если для любого выполняется неравенство 0 и имеется отличный от нуля вектор, для которого ;

неопределенной (), если существуют такие векторы, , что выполняются неравенства, ;

тождественно равной нулю (), если для любого выполняется .

Критерий Сильвестра. 1) Для того чтобы квадратичная форма с матрицей являлась положительно определенной необходимо и достаточно, чтобы все угловые миноры матрицы были положительны.

2) Для того чтобы квадратичная форма с матрицей являлась отрицательно определенной необходимо и достаточно, чтобы все угловые миноры матрицы нечетного порядка были отрицательны, а угловые миноры четного порядка — положительны.

Теорема (Достаточные условия безусловного экстремума) Если у дважды непрерывно дифференцируемой в стационарной точке функции ее второй дифференциал в этой точке является положительно определенной квадратичной формой, то точка является точкой строгого минимума, а если отрицательно определенной, то — точкой строгого максимума, если же — неопределенной формой, то экстремума в рассматриваемой точке нет.

Пример:

.

тогда.

положительно определена при любом Х, поэтому точка (2, 4, 6) является точкой локального минимума, а так как это единственная стационарная точка, то она же является и точкой глобального минимума.

Таким образом, для решения задачи оптимизации классическим методом необходимо решить систему уравнений, что невозможно сделать аналитически за исключением очень узкого класса таких систем (например, система линейных уравнений невысокого порядка). Затем придется еще устанавливать определенность гессиана, что тоже является совсем нетривиальной задачей в случае больших размерностей. Все это приводит к необходимости разрабатывать итерационные процедуры решения задач оптимизации.