Показатели изменения уровней ряда

Для оценки направления и величины изменения признака с течением времени используются показатели изменений уровней ряда, или показатели динамики. Расчет этих показателей основан на сравнении уровней динамического ряда между собой. Уровень текущего или более позднего периода, который сравнивается с другим уровнем, называется сравниваемым уровнем. Уровень того периода, с которым производится сравнение, называют базой сравнения или базовым уровнем. Если каждый уровень сравнивается с предыдущим, то полученные показатели называются ценными. Если все уровни сравниваются с одним и тем же уровнем, выступающим как постоянная база сравнения, то полученные при этом показатели называются базисными. Для измерения абсолютных и относительных изменений уровней ряда рассчитывают ряд индикаторов.

Абсолютное изменение (скорость роста или снижения) показывает, на какую величину в абсолютном выражении сравниваемый уровень больше или меньше базисного. При увеличении значения уровня говорят об абсолютном приросте (положительное значение), при уменьшении об абсолютном сокращении (отрицательное значение). Если за базу сравнения принимается предыдущий уровень, то получаем цепное абсолютное изменение. При сопоставлении всех уровней ряда с первым уровнем в ряду (или с уровнем, выбранным за базу по другим причинам) получают базисные абсолютные изменения. Между цепными и базисными абсолютными изменениями существует следующая зависимость: сумма цепных абсолютных изменений равна базисному абсолютному изменению последнего периода.

Ускорение — это величина, на которую сравниваемая скорость (абсолютное изменение) больше или меньше предыдущей. Рассчитывается как разность соответствующих абсолютных изменений; применяется только к цепным показателям.

Коэффициент изменения — это величина, которая показывает, во сколько раз увеличился уровень по сравнению с базисным (коэффициент роста) или какую часть базисного уровня составляет сравниваемый уровень (коэффициент сокращения). Относительное изменение чаще всего выражается в процентах (коэффициент роста или сокращения умножается на 100), тогда говорят о темпе изменения (темпе роста или темпе сокращения). Если уровень сравниваемого периода во много раз больше базисного уровня, то следует использовать коэффициент роста и выражать изменение в разах; если произошло уменьшение уровня — то темп сокращения, выраженный в процентах. Коэффициенты изменения могут рассчитываться цепные и базисные. Произведение цепных коэффициентов изменения дает базисное изменение последнего периода.

Темп прироста является вспомогательным показателем, он равен темпу изменения за вычетом ста процентов. Темп прироста показывает, на сколько процентов уровень сравниваемого периода больше или меньше уровня базисного периода; соответственно, он может быть положительной или отрицательной величиной. Данный индикатор может быть выражен и как отношение абсолютного изменения к уровню базисного периода, поэтому его иногда называют относительным приростом. Если коэффициент роста является большой величиной, то темп прироста теряет свое значение и не применяется.

Перечисленные показатели для развернутой характеристики временных изменений рекомендуется использовать вместе: абсолютное изменение дает представление о произошедших изменениях в единицах измерения самого признака, а относительное позволяет сравнить степень этих изменений в сравнении с другим периодом времени или с другими признаками. Разная база сравнения (цепные и базисные) также расширяет аналитические возможности. Кроме того, для обобщающей характеристики изменений в динамике исследуемого явления определяют средние показатели. Можно выделить средние уровней ряда и средние изменений уровней ряда.

Средний уровень ряда определяется следующим образом:

1) для моментного динамического ряда с равноотстоящими уровнями — по формуле средней хронологической.

где у — средний уровень; y_v…, у_п — уровни ряда; п — количество уровней ряда;

2) для интервального динамического ряда с равноотстоящими уровнями — по формуле средней арифметической простой.

где у — средний уровень; y_i — уровни ряда; п — количество уровней ряда;

3) для динамического ряда с неравноотстоящими уровнями — по формуле средней арифметической взвешенной.

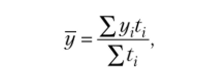
где у — средний уровень; у, — уровни ряда; Ц — промежуток времени.

Основными видами средних из показателей изменений уровней ряда являются следующие.

1. Среднее абсолютное изменение, или средняя скорость изменения (рассчитывается как средняя арифметическая из показателей скорости изменения за отдельные промежутки времени и показывает, на сколько в среднем в единицу времени увеличивается или уменьшается уровень ряда в своих единицах измерения):

где Д, — цепные абсолютные изменения; у_п> у_х — конечный и начальный уровни ряда; п — количество уровней ряда.

2. Средний коэффициент изменения (вычисляется по формуле средней геометрической из коэффициентов изменения за отдельные периоды и показывает, во сколько раз в среднем за период изменялись уровни динамического ряда):

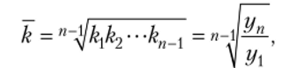
где kj — цепные коэффициенты изменения; у_п, у_{ — конечный и начальный уровни ряда; п — количество уровней ряда.

3. Средний темп прироста (определяется на основании данных о среднем темпе изменения и показывает, па сколько процентов в среднем изменяется уровень ряда):

где k — средний коэффициент изменения; Т — средний темп роста.

Следует обратить внимание на обоснованное использование средних показателей динамики. Данные величины могут давать содержательную оценку изменений только в том случае, когда эти изменения сравнимы между собой, когда их изменчивость невелика. В противном случае рассчитываемые средние величины абсолютно формальны и никакой аналитической ценности не имеют.