Методы Ньютона. 
Итерационные методы решения алгебраических и трансцендентных уравнений

Наряду с методами половинного деления и простой итерации существуют и другие, более сложные и эффективные итерационные методы. Прежде всего к ним относится группа методов, которые связаны с именем Ньютона. Рассмотрим два их них — метод касательных и метод хорд.

Оба метода основаны на следующем приеме. Пусть уравнение (1) имеет единственный корень на отрезке. Преобразуем его к равносильному уравнению.

(15).

где — любая функция, определенная на отрезке и не обращающаяся на нем в нуль. Осуществляя различными способами выбор, можно получить, в частности, и указанные методы.

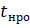
Метод касательных. Пусть в (15). Таким образом, итерационная последовательность строится с помощью рекуррентного соотношения.

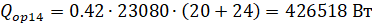
(16).

Вопрос о выборе начального приближения и гарантированной сходимости итераций решается просто, если функция удовлетворяет следующим условиям:

• 1) является дважды дифференцируемой на отрезке ;
• 2) обе производные — первая и вторая — не меняют знак на этом отрезке, т. е. функция монотонна и не меняет характера выпуклости; ситуация иллюстрируется одним из вариантов на рис. 7.

В такой ситуации за берется тот конец отрезка, на котором функция и ее вторая производная имеют одинаковые знаки, т. е. выполняется условие. Очевидно, что это левый конец на рис. 8, а и г и правый конец на рис. 7, б и в.

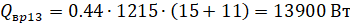
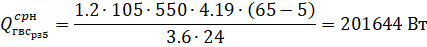
Допустим в дополнение к сделанным ранее предположениям, что также непрерывна на. Докажем, что отображение, соответствующее формуле (16), является сжимающим в некоторой окрестности корня уравнения. Для этого, как показано выше, достаточно, чтобы в указанной окрестности имело место неравенство. Вычислим производную.

.

Непосредственно в корне имеем.

.

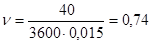
поскольку. Далее рассуждаем так: раз непрерывная функция обращается в нуль в некоторой точке, то существует такая окрестность этой точки, в которой, что и требовалось доказать.

Для оценки расстояния от очередного приближения до корня можно использовать как общее соотношение (9), так и следующий прием по формуле Лагранжа Отсюда получаем.

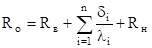
(17).

Эта оценка очень удобна, поскольку, так или иначе, вычисляется по мере нахождения членов рекуррентной последовательности (9).

Можно показать, что если имеет на непрерывную вторую производную, то погрешности на n — м и (n+1) — м шагах связаны неравенством.

. (18).

Таким образом, вычислительный алгоритм, заданный формулой (15), имеет квадратичную скорость сходимости.

Рассмотренный метод называется методом касательных потому, что если обратиться к графической иллюстрации (рис.8), то точка, определяемая по формуле (16) при n=0, есть точка пересечения касательной, проведенной к графику функции в точке с абсциссой, с осью абсцисс.

Каждому члену итерационной последовательности (16) соответствует точка пересечения касательной, проведенной к графику функции в точке с абсциссой, определяемой предыдущим членом последовательности, с осью абсцисс.

Уточнить корень уравнения методом касательных на отрезке [0,4;0,5] с заданной точностью.

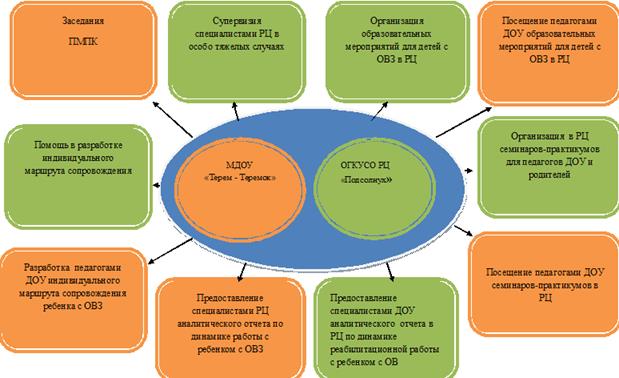
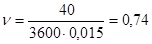
Результат работы программы:

Метод хорд. Реализуя метод касательных, при каждой итерации необходимо вычислять значение не только одной функции, но и ее производной .

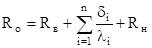
Если положить в (15), а в качестве с взять тот конец промежутка, на котором, то приходим к итерационному методу:

(19).

называемому методом хорд (или методом секущих).

В качестве в этом случае следует принять тот конец промежутка, который остался после выбора c (т.е. если, то или наоборот). Далее последовательность строится по формуле (19). оценка степени приближения к корню возможна с помощью неравенства (17). (Оно было получено с помощью формулы Лагранжа, не зависящей от рассматриваемых методов) Геометрический смысл метода (благодаря которому он получил название) проиллюстрирован на рис. 9. В данном случае, , соответствует точке пересечения хорды, соединяющей концы кривой, с осью абсцисс. Далее находится точка на кривой с абсциссой, проводится следующая хорда и т. д.

Рис. 9. геометрический смысл метода хорд.

Уточнить корень уравнения методом хорд на отрезке [0,4;0,5] с заданной точностью.