Построение карты высот с помощью алгоритма Diamond-Square

Самым же распространенным и дающим одни из самых реалистичных результатов является алгоритм diamond-square (или square-diamond), расширение одномерного алгоритма midpoint displacement на двумерную плоскость. Ландшафты, получающиеся с его помощью, называют фрактальными.

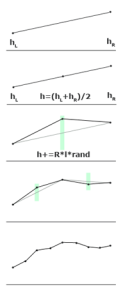
Рисунок 2.4. Построение ландшафта алгоритмом midpoint displacement.

Начнем с более простого алгоритма midpoint displacement. Как уже сказано, он работает не на двумерной плоскости, а на одномерном отрезке (поэтому с его помощью можно, например, создать линию горизонта). Изначально мы любым образом задаем высоту на концах отрезка и разбиваем его точкой посередине на два под-отрезка. Эту точку мы смещаем на случайную величину и повторяем разбиение и смещение для каждого из полученных под-отрезков. И так далее — пока отрезки не станут длиной в один пиксель (Рисунок 2.4). Важное замечание: случайные смещения должны быть пропорциональны длинам отрезков, на которых производятся разбиения. Например, мы разбиваем отрезок длиной — тогда точка посередине него должнаиметьвысоту.

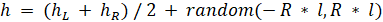
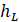
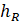
(и — высоты на левом и правом конце отрезка, а константа определяет «шероховатость» (roughness) получающейся ломаной и является главным параметром в данном алгоритме).

Обобщим этот алгоритм для двумерной карты высот. Начнем с присвоения случайных высот четырем углам всей карты целиком и разобьём её (для удобства предположим, что мы работаем с квадратной картой, причем её сторона является степенью двойки) на четыре равных квадрата. В каждом из них известно значение в одном из углов. Точка в центре получается усреднением высот всех 4 угловых точек, а каждая серединная точка на стороне большого квадрата — усреднением пары точек, лежащих на концах соответствующей стороны. Осталось применить немного шума — сдвинуть случайным образом центральную точку вверх или вниз (в пределах, пропорциональных стороне квадрата) — и повторять рекурсивно эти действия для полученных под-квадратов (Рисунок 2.5).

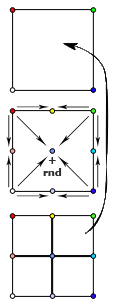
Рисунок 2.5. Построение карты высот двумерным алгоритмом midpoint displacement.

Это ещё не diamond-square — данный алгоритм, как правило, тоже называют алгоритмом midpoint displacement и несмотря на то, что он дает уже относительно приемлемые результаты, в получившейся карте высот без особого труда можно заметить линейность.

Алгоритм diamond-square — тот самый, который позволяет получать «настоящие» фрактальные ландшафты — отличается от двумерного midpoint displacement тем, что состоит из двух шагов. Первый — т. н. «square» — точно так же определяет центральную точку в квадрате путем усреднения угловых и добавлением собственно displacement’а — случайного отклонения. Второй же шаг — «diamond» — призван определить высоту точек, лежащих на серединах сторон. Здесь усредняются не две точки — «сверху» и «снизу» (если говорить о точках на вертикальной стороне), но и пара точек «слева» и «справа» — то есть еще две полученных на шаге «square» центральных точки. Важно заметить, что эти две высоты, которые были получены на предыдущем шаге, должны быть уже посчитаны — поэтому расчет нужно вести «слоями», сначала для всех квадратов выполнить шаг «square» — затем для всех ромбов выполнить шаг «diamond» — и перейти к меньшим квадратам (Рисунок 2.6).

Кроме необходимости использовать, обход в ширину вместо обхода в глубину, есть ещё одна тонкость — ситуация на краях ландшафта. Дело в том, что на этапе «diamond» алгоритм использует высоту точек, которых находятся за пределами текущего квадрата и, возможно, всей карты. Варианта два: либо считать эти высоты равными 0 (или 1, или любой другой константе), либо представить, что плоскость свернута в тор и, пытаясь узнать высоту точки, лежащей на 64 пикселя левее левой границы карты, мы узнаем высоту точки, отстоящей на 64 точки от правой границы. Реализуется очень просто (как, впрочем, и первый вариант) — поможет взятие координат по модулю, равному размеру карты.

Алгоритм Diamond-Square дает наиболее реалистичные результаты, хотя и не лишен некоторых недостатков. Например, создав карту, которая хорошо выглядит при сильном приближении — при просмотре целиком можно увидеть множество мелких островков (а то и вовсе сплошной шум) вместо нескольких больших материков и океанов. Самоподобия не выходит. Исправить это можно различным комбинированием фрактальных ландшафтов разного масштаба. Их значения можно перемножать, складывать, использовать различные коэффициенты или, например, привнести данные, полученные с помощью диаграммы Вороного.

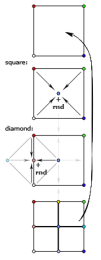
Рисунок 2.6. Построение карты высот алгоритмом Diamond-Square.