Вогнутые функции полезности

Определение

Вещественная функция g, определенная на интервале (а, Ь) вещественной прямой, называется вогнутой на (а, Ь), если функция (-g) выпукла на (а, Ь). Таким образом, g вогнута па (а, Ь), если для любых двух точек х и у из (а, Ь) и любого числа а, такого, что 0 < а < 1, выполнено неравенство.

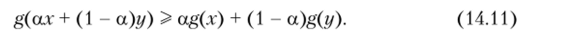
Говорят, что функцияgстрого вогнута па (я, Ь), если функция (-g) строго выпукла.

Предположим, что функция полезности строго вогнута на интервале (а, Ь) денежных выигрышей, как показано на рис. 14.2.

В этом случае из неравенства Йенсена следует, что нужно предпочесть фиксированный выигрыш г из интервала (а, Ь) игре со случайным выигрышем ?, из (а, Ь), для которого Е = Ь_>. Возрастание функции полезности выражает правило «чем больше, тем лучше», ее вогнутость — неприятие риска.

Обратите внимание!

Лицо со строго вогнутой функцией полезности предпочитает избегать риск (от англ, risk averse).

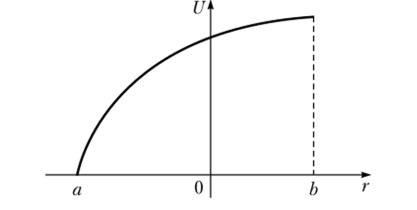
Рис. 14.2. Строго вогнутая функция полезности 164.

Функции полезности большинства индивидуумов вогнуты, по крайней мере, в случае больших выигрышей или больших проигрышей.

Рассмотрим вопрос о страховании. Люди страхуют свое имущество потому, что предпочитают уплатить фиксированную сумму г > 0 риску потерпеть большой убыток h с весьма малой вероятностью е. Другими словами, люди приобретают страховой полис, предпочитая фиксированный выигрыш -г игре, доставляющей с вероятностью е доход -h и никакого дохода с вероятностью 1 — е. Это предпочтение выражается соотношением.

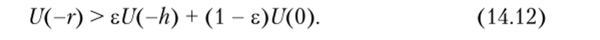
Функции U не обязательно быть вогнутой на всем интервале, для того, чтобы соотношение (14.12) было верным для одного данного значения г.

Страховая компания играет часто (продает много полисов) и имеет достаточно большие ресурсы. Следовательно, в отличие от отдельного полиса, функция полезности страховой компании U_act является приблизи тельно линейной функцией от денежного выигрыша. Поэтому U_an можно выбрать так, чтобы U_act(r*) = г* на соответствующем интервале. При продаже страхового полиса ожидаемый выигрыш компании должен быть выше нуля — ее выигрыша при несостоявшейся сделке. Поскольку ожидаемый выигрыш от продажи страхового полиса равен получаемой сумме г без средней суммы eh, выплачиваемой, но полису, то страховая компания выбирает сумму г такой, чтобы.

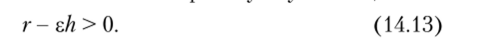
Страховой полис продается при одновременном выполнении обоих неравенств (14.12) и (14.13).

Неприятие риска обычно превалирует в экономике, примером чего может быть финансовый рынок или спрос на страхование. Как инвесторы, так и люди, страхующие имущество, соглашаются платить за избавление от риска. Однако в некоторых ситуациях принятия решений наблюдается, наоборот, поиск риска (лотереи, азартные игры). Поэтому функции полезности могут принимать совершенно различные формы.

Еще в классической модели М. Фридмана и Л. Дж. Сэвиджа (Friedman, Savage)^[1] была использована S-образная функция полезности, выпуклая в области доходов и вогнутая в области потерь, для объяснения поведения человека, одновременно покупающего лотерейные билеты (любовь к риску) и страховые полисы (неприятие риска). Заметим, что здесь идет речь о крупных потерях н выигрышах. В области меньших значений (соответствующих обычному для данного человека масштабу потерь и приобретений) отмечается противоположный эффект: любовь к риску перед лицом потерь п неприятие риска при перспективе приобретений. Люди могут демонстрировать стремление рисковать, чтобы избежать возможных потерь, и одновременно предпочитать верное получение средних сумм по сравнению с игрой, если в ней нет шанса выиграть очень много. На рис. 14.3 приведена форма функции полезности, которая соответствует отношению к риску, выявленному Д. Канеманом и Л. Тверски (Kalineman, Tversky)^[2] в результа;

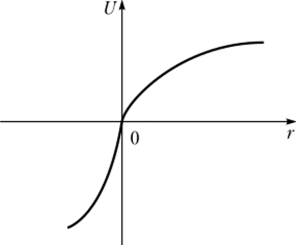
Рис. 143. Функция полезности, выпуклая в области потерь и вогнутая в области приобретений.

те эксперимента. Эта функция более «крута» в области потерь по отношению к некоторой точке отсчета, взятой за ноль на рисунке. Такая форма функции соответствует так называемым «эффекту отражения» (от англ. reflection effect) и «неприятию потерь» (от англ, loss aversion).

«Эффект отражения» заключается в том, что люди, с одной стороны, становятся все более безразличны к получению еще одного рубля по мере того, как заходит речь о получении все больших сумм, а с другой стороны, становятся все более безразличны к потере одного рубля по мере того, как речь заходит о все больших потерях. То есть происходит аналогичное «насыщение» в области приобретений и потерь.

«Неприятие потерь» — эффект, состоящий в том, что люди более чувствительны к потерям, чем к приобретениям. Ему соответствует более «крутая» форма функции в области отрицательных значений (потерь). В последние десятилетия концепция неприятия потерь приобретает все большую важность в экономике. Этот эффект наблюдается как при принятии решений в условии риска, так и в безрисковых ситуациях.

Изучая правила принятия решений, необходимо принимать во внимание, в каких условиях для принятия решения изначально находится Л IIP. Другими словами, кто фактически делает выбор — миллионер или студент, предпочитает ли он риск или стабильность, хотя его предпочтения уже частично определены тем выбором, который он сделал. Ранее об этой сложности упоминалось в разговоре о построении ценности по точкам. Теория полезности позволяет принимающему решение влиять на денежный результат исходов, согласно своим оценкам их полезности. Одно и то же правило в данном случае приводит к разным решениям у разных людей, каждый может приспосабливать процесс принятия решений к своим запросам. Как уже говорилось ранее, функция полезности должна отражать структуру предпочтений ЛИР.

Пример двух вариантов вложений 1000 условных денежных единиц (у.д.е.). По первому варианту (обозначим его х_{) без какого-либо риска можно получать 10% прибыли на вложенный капитал, т. е. через год сумма возрастет до 1100 у.д.е. По второму варианту (х₂) можно, либо потерять весь капитал, либо его удвоить через год. Ниже в табл. 14.3 представлены доходы для обоих случаев.

Доход в 1100 у.д.е. по 100-балльной шкале — около 55, если точка отсчета — 0, а верхний предел — 2000 у.д.е. Теперь рассмотрим, какова полезность 1100 у.д.е. для двух разных людей, принимающих решение.

Таблица доходов за один год для обоих случаев вложения.

Например, для студентки, у которой исходная сумма 1000 у.д.е. — последние деньги, их потеря невосполнима, поэтому полезность 1000 у.д.е. высока. Чтобы выразить ее в цифрах, попросим ее оценить вероятность Р максимального дохода (2000 у.д.е.) до того, как она примет решение и выберет альтернативу х₂. Если вероятность успеха х₂ мала, предположим, 0,1, то рисковать не стоит, лучше воспользоваться безрисковой альтернативой х_{. Однако, если вероятность успеха равна 1, тогда она воспользуется х₂, как наиболее предпочтительной. Где-то в интервале значения вероятности Р = = [0,1; 1J находится точка замены безрисковой х_{ более прибыльной, но опасной х₂. Значение вероятности, где происходит смена альтернативы, представляет собой оценку полезности 1100 у.д.е. В ситуации со студенткой допустим, Р = 0,95; тогда полезность.

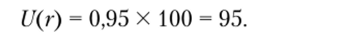
Таким образом, денежная шкала: 0 у.д.е. — 1100 у.д.е. — 2000 у.д.е. была заменена на шкалу полезности: 0 — 95 — 100.

Второй инвестор обладает капиталом в 500 000 у.д.е. Потеря 1000 у.д.е. вряд ли серьезно ударит по его карману, и риск большой роли не играет. Поэтому в данном случае тоже устанавливается значение вероятности Р, когда один вариант решения может быть заменен на другой. Для данного инвестора, допустим, Р = 0,2. То есть если вероятность успеха меньше 0,2, то стоит остановиться на альтернативе^ и ограничиться доходом в 1100 у.д.е. Если же Р > 0,2, тогда выбирается альтернатива х₂₁ т. е. полезность 1100 у.д.е. будет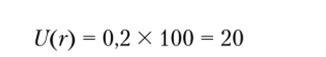

и денежная шкала: 0 у.д.е. — 1100 у.д.е. — 2000 у.д.е. заменяется на шкалу полезности: 0 — 20 — 100 у.д.е.

Таким образом, одна и та же денежная шкала может быть заменена разными шкалами полезности в зависимости от возможностей и критериев инвесторов.

Для того, чтобы проиллюстрировать преимущества шкалы полезности по сравнению с денежной шкалой, рассмотрим другой пример, в котором используется правило максимизации математических ожиданий.

Пример вариантов вложений с учетом полезностей. Допустим, некоторый господин N накопил 5000 у.д.е., чтобы купить дом в следующем году. И вдруг знакомый предлагает ему инвестировать эти деньги в его бизнес. В случае неудачи господин N потеряет 5000 у.д.е. и возможность купить дом. В случае успеха через год он получит 30 000 у.д.е. Специалист по маркетингу оценивает вероятность успеха альтернативы, связанной с вложением денег в бизнес (обозначим ее х,), в 0,3. Существует также другой вариант (обозначим его х₂) — положить деньги в банк иод 9% годовых, и данное решение не сопряжено для господина N ни с каким риском (табл. 14.4).

Таблица 14.4

Доходы при различных выбранных альтернативах.

По денежной шкале альтернатива, связанная с инвестированием денег в бизнес, дает наибольший ожидаемый доход. Использование принципа максимизации ожидаемого дохода подтаклкивает господина N выбрать именно эту альтернативу, которая, однако, влечет за собой существенный риск: в случае потери денег покупка дома останется лишь мечтой.

Шкала полезности для данного примера выглядит следующим образом: 0 — наименьший доход — 0 у.д.е.; 100 — наибольший доход — 30 000 у.д.е. То есть t/(0) = 0 и ?/(30 000) = 100. На практике неважно, как будет градуирована шкала полезности — от 0 до 100 или от 0 до 1, имеет значение лишь соразмерность. Для дохода 5450 у.д.е. не требуется оценка полезности. Нужно только определить, какова должна быть вероятность дохода 5450 у.д.е., если господин N посчитает его настолько же привлекательным, насколько и доход 30 000 у.д.е. с вероятностью Р и 0 с вероятностью (1 — Р). Предположим, для него достаточна вероятность по меньшей мере 60% успеха, т. е. Р = 0,6, тогда полезность 5450 у.д.е.

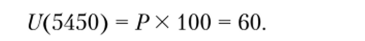
Оценки полезности для этого примера представлены в табл. 14.5.

Таблица 145

Полезности при различных выбранных альтернативах.

Вложение денег в банк — альтернатива с наибольшей ожидаемой полезностью. Однако это решение прямо противоположно выбору, сделанному на основе критерия максимизации ожидаемого дохода. Причиной этого является риск, связанный с возможным исходом бизнеса. График, позволяющий наглядно оценить риск с учетом соотношения полезности и доходов, представлен на рис. 14.4.

На рис. 14.4 прямой линией соединены точки, соответствующие значениям полезности ?/(0) и ?/(100). Если оценка полезности ?/(5450), соответствующей доходу 5450 у.д.е., находится выше этой линии, то ЛИР (в дан;

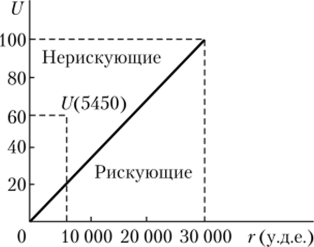
Рис. 14.4. Графическая интерпретация соотношения полезности и доходов.

ном случае, господин N) принадлежит к числу тех, кто избегает риска; если ниже, то наоборот. Как видно из графика, в условиях данной задачи господин N_y принимающий решение инвестировать 5000 у.д.е. в банк, относится к нерискующим или избегающим риск.

Данный пример демонстрирует преимущества шкалы полезности по сравнению с оценками денежных доходов. При его решении сначала был использован критерий максимизации дохода, затем произведена переоценка доходов с помощью оценок полезности, а затем применено правило максимизации ожидаемой полезности. Очевидно, что идея оценки ожидаемой полезности является универсальной и может быть использована для решения задач с несколькими допустимыми альтернативами.

• [1] Friedman М., Savage L.J. The Utility Analysis of Choices Involving Risk // Journal ofPolitical Economy. 1948. 56(4). P. 279−304.
• [2] Kahneman D., Tversky A. Advances in Prospect Theory: Cumulative Representation ofUncertainty //Journal of Risk and Uncertainty. 1992. 5. P. 297—323.