Сравнение алгоритмов бикластеризации

Сравнение алгоритмов бикластеризации проводилось по двум основным направлениям: скорость работы и общий «вклад» найденных алгоритмами бикластеров в исходную матрицу. Для подсчёта «вклада» использовалась бикластерная модель, предложенная Миркиным и Крамаренко вместе с алгоритмом BBox.

В данной модели матрица «остатков» (residuals) для набора бикластеров и исходной матрицы определяется по следующей формуле:

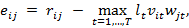
где — бинарные векторы принадлежности строк к множеству и столбцов к множеству соответственно. Таким образом, для подсчёта элемента матрицы остатков, нужно найти бикластер с наибольшей плотностью, который содержит данный элемент, то есть. Говоря менее формально, мы рассчитываем для каждого элемента исходной матрицы степень его «присутствия» в полученных бикластерах.

Далее, для подсчёта общего «вклада» мы считаем сумму квадратов остатков по всей матрице и делим на сумму квадратов элементов исходной матрицы:

.

1) Время выполнения Время работы алгоритмов бикластеризации сравнивалось на квадратных входных матрицах разного размера.

Как и в случае с мемоизацией, тестовые матрицы генерировались при помощи генератора случайных чисел.

Таблица 3. Сравнение алгоритмов спектрального разложения и жадного алгоритма Greedy BBox. Время представлено в секундах.

В связи с тем, что алгоритм спектральной бикластеризации требует указания количества бикластеров, на которое нужно разбить входную матрицу, в таблице представлены результаты анализа времени работы по выделению 10, 50 и 100 бикластеров данным методом. Из таблицы видно, что время работы жадного алгоритма матрицы растёт намного быстрее времени работы спектрального метода по мере увеличения размера входной. В таблице не приведено время работы алгоритма BBox, так как он значительно проигрывает по скорости конкурентам (обработка матрицы размеров 200×200 занимает около 440 секунд). Также стоит отметить, что алгоритм Greedy BBox работает быстрее на бинарных матрицах, чем на вещественных, чего нельзя с однозначностью сказать про спектральный метод.

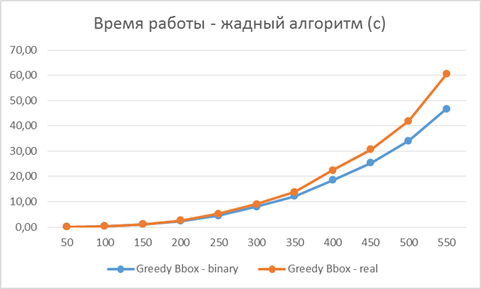
Рисунок 2. Время работы алгоритма GreedyBBox в секундах на случайных входных данных.

2) «Вклад» бикластеров.

В данном разделе для экспериментирования с алгоритмами для бикластерного анализа использовалась коллекция аннотаций к научным статьям, содержащая 2971 аннотацию. Данная коллекция была получена при помощи выгрузки аннотаций из электронной библиотеки IEEE Xplore. Для поиска данных аннотаций в электронной библиотеке использовался текстовый запрос «cluster analysis», поэтому данная коллекция связана с темой «кластерного анализа». Ключевые словосочетания из этой коллекции были выделены по гибридному алгоритму (модифицированный TextRank в сочетании с частотным анализом), представленному во второй главе.

Также для этой коллекции были загружены ключевые слова, предоставляемые самой библиотекой IEEE Xplore, включая термины, использованные для индексирования в базе данных Inspec (удалось получить для 2622 статей), и авторские ключевые слова (удалось получить для 1777 статей).

Таблица 4. Сравнение алгоритмов по общему «вкладу».

Для составления таблицы 4 было проведено 5 испытаний с различными параметрами:

• 1) Анализ матрицы схожести между ключевыми фразами, составленной по метрике релевантности Okapi BM25 и пороговым значением релевантности равным 0,15;
• 2) Анализ матрицы схожести между ключевыми фразами, составленной по методу АСД и пороговым значением релевантности равным 0,2;
• 3) Анализ матрицы схожести между ключевыми фразами, полученными из библиотеки IEEE Xplore для коллекции статей по кластерному анализу. Использовались фразы из тезауруса базы данных Inspec — controlled Inpsec terms. Здесь не указано пороговое значение, так как составленные вектора релевантности являются бинарными (фраза релевантна для статьи, если так указано в базе данных Inspec);
• 4) Анализ матрицы релевантности, составленной по метрике Okapi BM25;
• 5) Анализ бинарной матрицы релевантности для авторских ключевых фраз.

Из таблицы 4 можно видеть, что разработанный жадный алгоритм бикластеризации и алгоритм BBox сильно превосходят по точности («вкладу») алгоритм спектрального разложения. В таблице также представлены результаты для бикластеров, найденных по алгоритму GreedyBBox и отфильтрованных на основе схожести между собой (см. раздел 2.5.). Можно видеть, что фильтрация бикластеров не только не ухудшила показателей «вклада», но даже улучшила его в некоторых случаях — фильтрация производилась при пороге схожести по коэффициенту Жаккарда равном 0,7. Это связано с тем, что после фильтрации в итоговой матрице остатков получается меньшее количество отрицательных элементов, чем при учёте всех бикластеров.

Что касается сравнения алгоритмов BBox и GreedyBBox, таблица 4 показывает неоднозначные результаты: в двух случаях BBox заметно опережает жадный алгоритм, в одном лучший показатель у алгоритма GreedyBBox, а в двух других показатели примерно равны. Эти результаты отражают различие в подходах к выделению бикластеров: BBox находит только локально-оптимальные бикластеры, тогда как GreedyBBox находит новые бикластеры практически на каждой итерации, но многие из них могут сильно отличаться от оптимальных, а значит, скорее всего, вносят малый «вклад» в общий результат. Всё же, полученный результат показывает, что новый жадный алгоритм способен конкурировать с BBox, при этом значительно превосходя его по скорости работы.