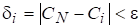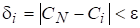Сравнение оценок. 
Неравенство Рао — Крамера

С помощью различных методов мы получаем множество оценок и нам нужно определить лучшие из них. Для сравнения оценок рассмотрим два подхода.

Среднеквадратический подход Пусть X₁, X₂,…, X_n выборка объема п из семейства распределений {p (t), ¹} и ^*₁, ^*₂ — две оценки неизвестного параметра .

Определение 1. Оценка ^*₁ лучше, чем ^*₂, если выполняется

Отметим, что если в определении 1 знак, , то получим понятия: «^*₁ не хуже», «хуже», «не лучше», чем ^*₂, соответственно.

Если h () = E*— смещение оценки *, то.

Так как для несмещенных оценок ^*₁ и ^*₂ смещение h() = 0, то в определении 1 величины E (*_i— )² заменяются на D*_i, i = 1, 2. Тем самым, сравнение несмещенных оценок сводится к сравнению дисперсии этих оценок.

Определение 2. В классе несмещенных оценок неизвестного параметра оценка * с минимальной дисперсией называется эффективной оценкой.

Асимптотический подход Пусть ^*₁ и ^*₂ две асимптотически нормальные оценки, т. е.

или Определение 1. Оценка ^*₁ лучше, чем ^*₂, если ²₁ < ²₂.

Естественно асимптотический подход менее предпочтителен, поскольку может быть применен в случае выборки большого объема и только в классе асимптотически нормальных оценок.

Пример. Пусть X₁, X₂,…, X_n выборка из показательного распределения Г_{, 1}, = — неизвестный параметр. В 3.4.1 мы получили две оценки.

Без доказательства заметим, что эти оценки асимптотически нормальны с коэффициентами ²₁ = ² и ²₂ = 5/4 ².Сравнив ²₁ и ²₂ мы видим, что оценка ^*₁ лучше, чем ^*₂.

Определение 2. В классе асимптотически нормальных оценок параметра оценка * с минимальным коэффициентом ² называется асимптотически эффективной оценкой.

Неравенство Рао — Крамера Попытаемся указать нижнюю границу дисперсии D* оценки *. Этот вопрос решается с помощью неравенства Рао — Крамера.

Пусть X₁, X₂,…, X_n выборка из семейства распределений {p (t), ¹}. Рассмотрим функцию L (t,) = ln p (t) и найдем ее производную по :

Предположим, что выполнено некоторое условие регулярности (R):

а) в случае распределения непрерывного типа функции p (t) непрерывно дифференцируемы по для почти всех t, а интегралы

существуют и непрерывны по ;

б) в случае распределения дискретного типа существуют частные производные p (t) /, а ряды

где p (i)—вероятности принятия значений i, дискретной случайной величины.

I ()—называется информационным количеством Фишера. Без доказательства (его можно найти в [4]) сформулируем следующую теорему.

Теорема (неравенство Рао — Крамера). Пусть выполнено условие ®. Тогда для оценки * неизвестного параметра справедливо следующее неравенство

Следствия теоремы.

При выполнении условий теоремы справедливо неравенство

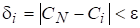
если же * — несмещенная оценка, то справедливо неравенство.

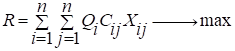
2. Если выполнено условие ® и в неравенстве Рао-Крамера достигается равенство, то * — эффективная оценка в классе оценок со смещением h (), т. е.