Применение микрокалькулятора при решение задач по математике

Микрокалькуляторы в настоящее время находят всё большее применение при решении задач. Освобождение учащихся от однообразной вычислительной работы позволяет уделить большее внимание самому алгоритму вычислений, сделать занятия более творческими. Появляется возможность решать задачи с реальными числовыми данными. Высокая точность и быстрота вычислений позволяет широко и систематически использовать в учебном процессе математический эксперимент для активизации познавательной деятельности учащихся. Появляется возможность знакомить учащихся с достаточно общими методами поиска и обоснования решения сложных нестандартных задач. Рассмотрение таких задач на занятиях без использования программируемых микрокалькуляторов методически не оправдано, потому что их решение сильно затруднено, а в ряде случаев невозможно. Калькуляторы помогают на более высоком уровне организовывать индивидуальную и коллективную работу учащихся. Микрокалькулятор является надёжным и удобным средством поэтапного контроля правильности выполнения тождественных преобразований выражений с переменными.

Программируемые микрокалькуляторы позволяют эффективно в комплекте использовать различные методы поиска решения задач.

Особо следует отметить роль калькуляторов при решении уравнений. Их систематическое применение при работе над уравнениями коренным образом изменяет её обучающее содержание. Калькулятор даёт возможность применять при решении самых различных уравнений общий функциональный метод, основанный на систематическом комплексном использовании свойств всех функций, изучаемых в школе. При таком подходе к работе над уравнениями у учащихся формируется не только общий метод их решения, но и происходит их систематическое комплексное повторение важнейших свойств изученных ими ранее функций. Последнее является самым существенным в методике обучения учащихся решению уравнений. 5].

С использованием микрокалькулятора делается практически универсальным и самым простым в применении метод интервалов решения неравенств.

В школе ученики изучают общие свойства непрерывных функций, применение которых в полном объёме позволяет существенным образом упростить поиск решения нестандартных уравнений. В самом деле, учащиеся знакомятся с достаточным условием монотонности функции, с правилами вычисления производных, с производной сложной функции. Отсюда непосредственно вытекают свойства суммы двух возрастающих (убывающих) функций, свойства сложных функций. Однако при решении уравнений и других задач прикладного характера эти важнейшие теоретические значения применения не находят и поэтому учениками усваиваются формально.

У учащихся должна постоянно формироваться культура работ над уравнениями, которая сводится к следующему. Приступая к решению уравнения, прежде всего необходимо попытаться выяснить, имеет ли оно корни. В необходимых случаях (для получения гипотезы о существовании корней) составляем таблицу значений функции при помощи калькулятора. Дело в том, что, доказать, что уравнение не имеет корней, часто гораздо проще, чем заниматься его преобразованиями, направленными на получение точных корней. Полученная таблица значений функции облегчает и выбор методов нахождения корней уравнения, напоминает о существовании свойств функции, на которые без таблицы мы не могли бы и не обратить внимание.

Следует заметить, что определение корней уравнения может оказаться более сложной задачей, чем решение уравнения. Поэтому часто приходиться отказываться от мысли отделить корни уравнения путём нахождения критических точек функции. Во многих случаях отделение корней упрощается с помощью метода «ступенек». Для этого уравнение преобразуется к виду возрастающие или убывающие функции на некотором промежутке). При помощи калькулятора составляются таблицы значений функций (с достаточно малым шагом). Работа над уравнением завершается уточнением отдельных корней.

Задача 1.Найти рациональные числа n и k, такие, что.

Решение. При помощи микрокалькулятора последовательно находим:

.

602+602,0007=1364,0007,.

Сравнив первое и последние из этих неравенств, получаем, что k=1 и n=2, т. е.

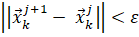
Задача 2. Сумма трёх первых чисел a, b, c равна нулю. Доказать, что число является квадратом целого числа.

Решение. Попытаемся получить гипотезу о каких-либо свойствах данного выражения путём рассмотрения частных случаев.

Если, например, a=1, b=2, то c=-3 и данное выражение равно. Если a=2, b=3,c=-5, то данное выражение равно Если a=-3, b=8, c=-5 и данное выражение равно .

Но как связаны значения a, b, c с основаниями квадратов ,? Легко заметить, что, Итак, появляется гипотеза, что.

.

если a+b+c=0. Полученная в результате математического эксперимента гипотеза легко доказывается.

Задача 3. Рассматриваются все возможные семизначные числа k с цифрами 1, 2, 3, 4, 5, 6, 7, записанными в произвольном порядке. Существуют ли среди этих чисел два таких числа m и n, что m делиться на n?

Решение. Сумма цифр числа k равна 28. Поэтому m и n не делятся на 3 и 6. Число 7 654 321 является наибольшим из чисел k, а число 1 234 567 -наименьшим из всех чисел k. Так как 7 654 321:1 234 567 6,3, то ясно, что при делении m на n может получиться только 2,4 или 5.

Если число m делиться на 5, то оно должно оканчиваться цифрой 5, поэтому первой цифрой числа m может быть только 6 или 7. Рассмотрим несколько примеров (вычисления ведутся при помощи микрокалькулятора):

7 643 215:5=1 528 643, 7 436 125:5=1 487 225, 7 432 165:5=1 486 433, 6 374 125:5=1 274 825, 6 142 375:5=1 228 475, 6 137 245:5= 1 227 449.

Замечаем, что все частные содержат цифру 8 или 9. Но почему? Да потому, что при данном условии при делении на 5 всегда приходиться делить число на 41, или 42, или 43, или 45 на 5. Выясним, существует ли равенство 2n=m или 4n=m. Рассмотрим примеры: 3 765 2=7 530 842,.

3 765 412 2=7 530 824, 1 654 372 2= 3 308 744, 2 134 567 2= 4 269 134,.

1 234 765 2= 2 469 530, 2 573 146 2=5 146 392.

После рассмотрения этих примеров становится понятным, что при умножении любого числа n на 2 получаем число с цифрой 8, если после 4 в числе n стоит цифра 1, 2 или 3. Если в числе n после цифры 4 стоит цифра 5, 6 или 7, то при его умножении на 2 получаем число с цифрой 9. Осталось выяснить, существует ли равенство 4n=m. Рассмотрим несколько примеров:

1 765 432 4= 7 061 728, 1 276 543 4= 5 106 172,.

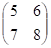
Во-первых, ясно, что число n может начинаться столько с цифрой 1 и не может оканчиваться цифрой 2, 7 или 5. Во-вторых, число m везде содержит цифру 0, 8 или 9. И это зависит от того, какие две цифры стоят в числе n после 2: 34, 35, 36, 37, 43, 45, 46, 47, 53, 54, 56, 57, 63, 64, 65, 67, 73, 74, 75, 76.

Таким образом, доказано, что задача не имеет решения.

Задача 4. Решить уравнение.

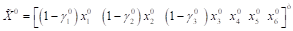
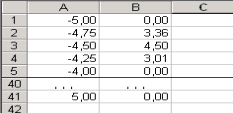
Решение. Положительная функция определена на промежутке (-1,0) и (0,1). Положительную функцию рассматриваем на и (0,1). Для получения гипотезы о числе корней уравнения составляем таблицу значений функций и :

x.	P (x)	F (x)	x	P (x)	F (x)
-1 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3 -0,2	11,4 8,33 7 6,25 5,77 5,46 5,24 5,10 5,05	6,08 5,97 5,83 5,65 5,41 5,08 4,58 3,75 2,08 0	0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 1	5 5,02 5,10 5,24 5,46 5,77 6,25 7 8,33	17,1 12,1 10,4 9,58 9,08 8,75 8,51 8,33 8,08

Функции и на (-1, -) убывают. Методом «ступенек «легко доказывается, на этом промежутке уравнение (1) корней не имеет. На (0,1) непрерывная функция возрастает, убывает. Число 0,8 является единственным корнем уравнения (1).

Данные вычисления следует применять при изучении алгебры в 7−9 классах с использованием возможностей применения малых вычислительных средств.