Рассмотренные и используемые термины

Машина Тьюринга.

Машимна Тьюмринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина).

Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.

Машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам преобразует входные данные с помощью последовательности элементарных действий.

Машина Тьюринга способна имитировать всех других исполнителей (людей или других живых существ) (с помощью задания правил перехода), каким-либо образом реализующих процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

В состав машины Тьюринга входит:

бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент),.

разделённая на ячейки,.

и управляющее устройство, способное находиться в одном из множества состояний.

Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга.

Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.

Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.

Описание машины Тьюринга Конкретная машина Тьюринга задаётся перечислением:

• · элементов множества букв алфавита A,
• · множества состояний Q
• · и набором правил, по которым работает машина.

Они имеют вид: qiaj>qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква aj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо ®, остаться на месте (N)).

Для каждой возможной конфигурации имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил).

Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.

Конечный автомат.

Конечный автомат — абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию.

Существуют различные способы задания конечного автомата. Например, конечный автомат может быть задан в виде упорядоченной пятерки:

где.

• · — входной алфавит (конечное множество входных символов), из которого формируются входные цепочки, допускаемые конечным автоматом;
• · — множество состояний;
• · — начальное состояние ;
• · — множество заключительных состояний ;
• · — функция переходов, определенная как отображение, такое, что, т. е. значение функции переходов на упорядоченной паре (состояние, входной символ или пустая цепочка) есть множество всех состояний, в которые из данного состояния возможен переход по данному входному символу или пустой цепочке (л).

Конечный автомат начинает работу в состоянии q₀, считывая по одному символу входной цепочки. Считанный символ переводит автомат в новое состояние в соответствии с функцией переходов. Читая входную цепочку x и делая один такт за другим, автомат, после того как он прочитает последнюю букву цепочки, окажется в каком-то состоянии q'.

Если это состояние является заключительным, то говорят, что автомат допустил цепочку x.

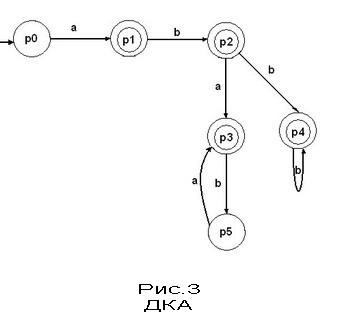
• · Детерминированным конечным автоматом (ДКА) называется такой автомат, в котором нет дуг с меткой е и из любого состояния по любому символу возможен переход в точности в одно состояние.
• · Недетерминированный конечный автомат (НКА) является обобщением детерминированного.