Линейные уравнения. 
Линейные уравнения

1) Решить систему линейных алгебраических уравнений, сделать проверку.

x + y — 3z = 0.

3x + 2y + 2z = -1.

x — y + 5z = -2.

РЕШЕНИЕ:

Решим систему по правилу Крамера, смысл которого состоит в том, что если определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:

алгебраический уравнение дифференциал интервал.

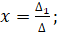
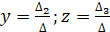
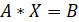
В матричной форме система имеет вид:, где.

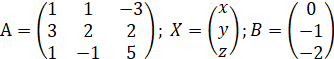
Вычислим определитель матрицы, А с помощью правила треугольников, которое гласит: определитель равен алгебраической сумме произведений элементов, расположенных на главной и побочной диагоналях и в вершинах треугольников с основаниями параллельными диагоналям. Произведения элементов, расположенных на побочной диагонали и в вершинах треугольников с основаниями параллельными ей, берутся со знаком минус.

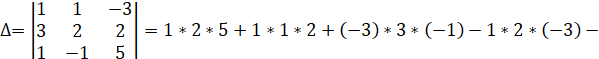
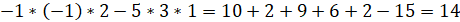
Составляем дополнительные определители, полученные из определителя системы, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:

; ;

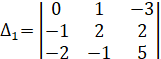
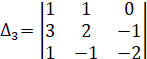
Находим данные определители:

• ?₁ = 0 * 2 * 5 + (-3) * (-1) * (-1) + (-2) * 1 * 2 — (-2) * 2 * (-3) — 0 * (-1) * 2 — 5 * * (-1) * 1 = 0 — 3 — 4 — 12 — 0 + 5 = -14
• ?₂ = 1 * (-1) * 5 + 1 * 0 * 2 + (-3) * 3 * (-2) — 1 * (-1) * (-3) — 1 * (-2) * 2 — 5 * 3 * * 0 = -5 + 0 + 18 — 3 + 4 — 0 = 14
• ?₃ = 1 * 2 * (-2) + 0 * 3 * (-1) + 1 * 1 * (-1) — 0 * 2 * 1 — 1 * (-1) * (-1) — (-2) * 3 * * 1 = -4 + 0 — 1 — 0 — 1 + 6 = 0

Решаем систему линейных уравнений:

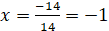
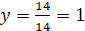
Решим систему линейных уравнений методом Гаусса.

Преобразуем расширенную матрицу системы:

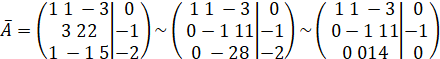
Получим систему линейных уравнений:

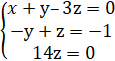
Из третьего уравнения находим .

Из второго уравнения находим .

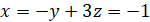
Из первого уравнения находим .

Выполним проверку:

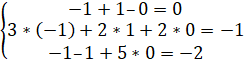
Ответ:;; .

2) Даны координаты точек A, B, C: A (7; -4; 1), B (12; -3; 1), C (10; 1; 5) .

Найти: 1) координаты векторов AB и AC;

• 2) длины векторов AB и AC;
• 3) угол между векторами AB и AC.

РЕШЕНИЕ:

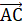
1) Координаты вектора и вычисляются следующим образом: из соответствующих координат конца вектора вычитаются соответствующие координаты начала вектора.

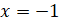
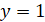
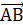
Вычислим координаты вектора :

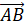
(x₂ — x₁; y₂ — y₁; z₂ — z₁) = (12−7; -3-(-4); 1−1) = (5; 1; 0).

Вычислим координаты вектора :

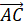
• (10−7; 1-(-4); 5−1) = (3; 5; 4).
• 2) Длина вектора равна корню квадратному из суммы квадратов его координат:

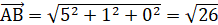
3) Угол между векторами заданными своими координатами, вычисляется по формуле:

==.

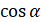
Угол между векторами и :

====.

.

Ответ: 1) (5; 1; 0) и (3; 5; 4); 2) и; 3) .

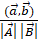
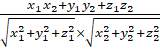
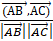
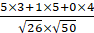
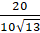
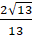
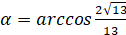
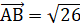
3) Даны координаты вершин треугольника ABC: A (-5; 0), B (7; 9), C (5; -5).

Найти: 1) длину стороны AB;

• 2) уравнение прямой, содержащей сторону AB, и ее угловой коэффициент;
• 3) уравнение прямой, содержащей высоту CD.

РЕШЕНИЕ:

1) Длина отрезка АВ находится по формуле:

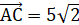
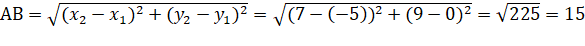
2) Уравнение прямой, проходящей через две данные точки:

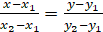
Подставим в формулу координаты точек, А и В:

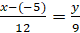
Уравнение прямой будет следующим:

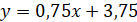
Угловой коэффициент равен 0,75.

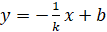
3) Высота CD перпендикулярна стороне треугольника AB, уравнение которой мы нашли выше. Тогда уравнение высоты CD, перпендикулярной АВ, будет иметь вид .

Подставим в это уравнение координаты вершины С:

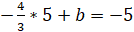
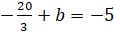
b = 5/3.

Тогда уравнение прямой, содержащей высоту CD будет иметь вид:

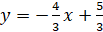
Ответ: 1) АВ = 15; 2) Уравнение прямой АВ:, угловой коэффициент k = 0,75; 3) Уравнение прямой, содержащей высоту CD: .

4) Решить графически систему линейных алгебраических неравенств.

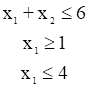
РЕШЕНИЕ:

Рассмотрим сначала простейшие неравенства x₁? 1 и x₁? 4. Нанесем прямые x₁ = 1 и x₁ = 4 на координатную ось. Знаки неравенства указывают, что решением для неравенства x₁? 1 является правая полуплоскость и сама прямая, а решением для неравенства x₁? 1 — левая полуплоскость и сама прямая.

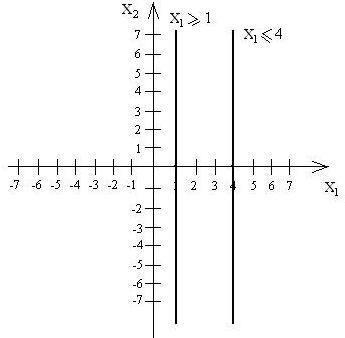
Третье неравенство решаем универсальным методом решения с подстановкой точки. Построим прямую x₁ + x₂ =6. Выбираем подопытную точку, например, (0; 0) и подставим ее координаты в наше неравенство: 0 + 0? 6. Получено верное неравенство, значит, точка (0; 0) и все точки данной полуплоскости удовлетворяют неравенству.

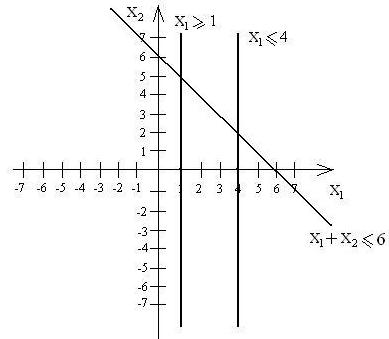
Общим решением системы неравенств станет заштрихованная фигура.

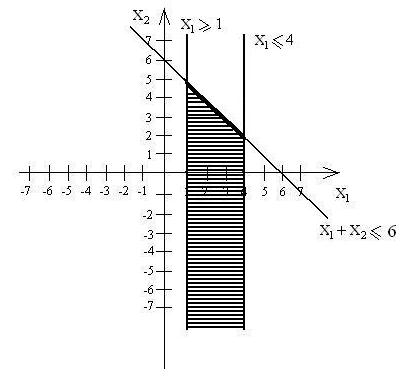
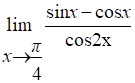
5) Найти пределы, .

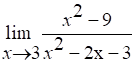
РЕШЕНИЕ:

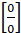
1)Для раскрытия неопределенности разложим числитель и знаменатель на множители:

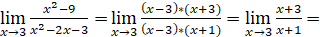
2) Для раскрытия неопределенности разложим знаменатель на множители, используя формулу:

=.

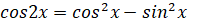
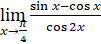
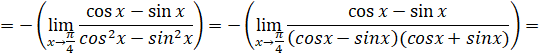
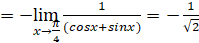
6) Найти производную и дифференциал функций.

.

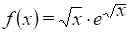
РЕШЕНИЕ:

1).

2).

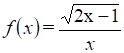
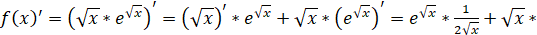
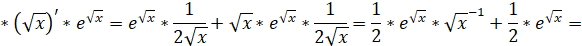
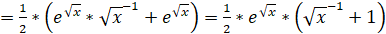
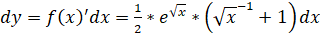
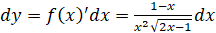
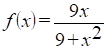
7) Исследовать функцию, построить график. Найти наибольшее и наименьшее значения функции на отрезке [-2; 2].

РЕШЕНИЕ:

1. Область определения функции:

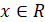
2. Функции нечетная, так как :

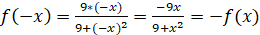
График функции симметричен относительно начала координат.

3. Точки пересечения с осями координат:

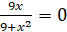
Если y = 0, то => x = 0.

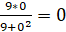
Если x = 0, то => y = 0.

График функции пересекает оси координат в точке (0;0).

4. Исследуем на экстремумы и монотонность. Вычисляем первую производную:

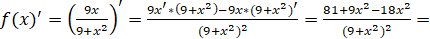
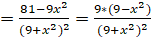
Находим критические точки:

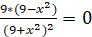
x₁ = 3, x₂ = -3.

Исследуем знак производной на интервалах, на которых критические точки делят область определения функции:

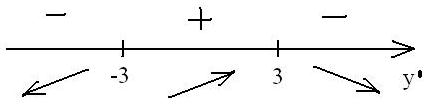
Функция убывает на интервалах (-?; -3), (3; +?), возрастает на интервале (-3; 3). При прохождении через точку -3 производная меняет знак с минуса на плюс, то есть это точка минимума, а при прохождении через точку 3 — с плюса на минус, соответственно это точка максимума.

5. Асимптоты.

Найдем наклонные асимптоты. y = kx + b.

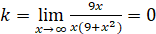
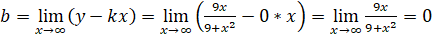
Вертикальных асимптот нет, горизонтальная асимптота y = 0.

5. Найдем интервалы выпуклости и точки перегиба графика функции.

Вычисляем вторую производную:

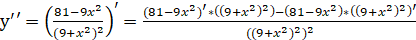
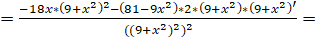
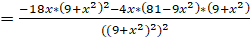
Находим точки, в которых вторая производная равна нулю:

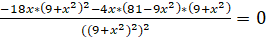
x = 0, x = -3v3, x = 3v3.

Исследуем знак производной на интервалах, на которых эти точки делят область определения функции:

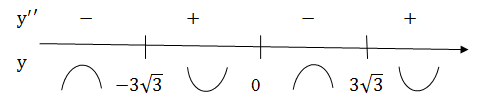
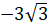
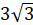
Функция выпукла вверх на интервалах (-?;), (0;), выпукла вниз на интервалах (; 0), (; +?). Так как при переходе через точки.

x₁ = 0, x₂ = -3v3, x₃ = 3v3 вторая производная сменила знак, то точки.

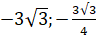
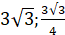
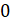
(), (), (0;) являются точками перегиба графика функции.

Строим график функции:

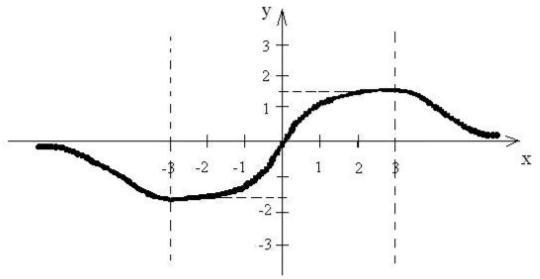
Для того, чтобы найти наибольшее и наименьшее значения функции на отрезке [-2; 2], необходимо вычислить значения функции на концах отрезка.