Сравнительный анализ алгоритмов моделирования пуассоновских ансамблей

Проведем сравнение алгоритмов моделирования пуассоновских ансамблей, построенных в главе 3 пособия [31].

Для оценки математического ожидания численно моделируется N траекторий. При приближенном вычислении математического ожидания (?) случайной величины? с конечной дисперсией а² по формуле 1 N

^ПР^И заданном уровне доверия (1 — е) имеет место соотно;

г=1.

шение [90].

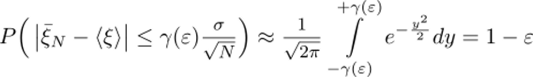
где 7(5) константа, определяемая выбором величины е. При е = 0.003 получаем 7(e) = 3, т. е. при достаточно большом N значение (?) с вероятностью р = 0.997 принадлежит доверительному интервалу.

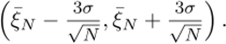
Чем больше дисперсия <�т, тем больший объем выборки Л^г требуется для вычисления оценки математического ожидания с заданной точностью.

В таблицах с результатами численных экспериментов приведены доверительные интервалы для оценки математического ожидания. Время расчета указано в секундах. Расчеты проводились на PC Intel Celeron,.

2.02 ГГц, 768 МБ.

Тест 1. Моделирование однородного пуассоновского процесса ?(?), t > 0 с интенсивностью Л. Известно, что Е?(?) = At. Для оценки математического ожидания моделировалось 10⁶ траекторий на интервале [0, Т, Т = 2.

Сравним два метода моделирования однородного пуассоновского процесса: метод 1 и метод 3 из параграфа 3.6 пособия [31]. Запишем эти методы применительно к данному тесту с указанием формул моделирования.

Метод 1:

• 1) моделируем целое к по закону Пуассона с параметром XT (по алгоритму 1.2 из [90]);
• 2) моделируем к точек {r,} -L₁ в интервале [0,Т] независимо с плотностью р (х) = ^ (по формуле ъ = otiT, где а₇; - независимые равномерно распределенные случайные величины на [0,1]);
• 3) упорядочим точки {т_г}^₌₁ и полагаем ?(т*) = г.

Метод 3:

1) моделируем последовательность независимых значений ti, 72,… с экспоненциальной плотностью р (х) = Хехр (-Хх) (по формуле.

Inai

Ti =——, где а_г — независимые равномерно распределенные слу;

А чайные величины на [0,1]);

2) полагаем U = ^У₌₁ ?{U) = г, пока ti < Т.

Результаты статистического моделирования приведены на рис. 1.29 и в табл. 1.18. На рис. 1.29 приведены точное математическое ожидание и.

его оценки, полученные обоими методами, на интервале [0,2] для Л = 0.6. Математическое ожидание оценивалось в точках ti = 0.02?_?_i, г = 1,…, 100, «о = 0.

В табл. 1.18 помещены полученные абсолютные погрешности оценки математического ожидания в последней точке и время счета для различных параметров Л.

Из табл. 1.18 видно, что при малых интенсивностях оба метода сравнимы по времени счета. При больших Л метод 1 считает дольше, так как много времени тратится на упорядочение моментов {т*}*₌₁.

Тест 2. Моделирование неоднородного пуассоновского процесса ?(«), t > 0 с интенсивностью X (t) = _me~^2t и Е?(?) = ^-(1 —e~^2t). Для оценки математического ожидания моделировалось 10⁶ траекторий на интервале [0,Т], Т = 2. Тест был просчитан тремя методами (из параграфа 3.7 пособия [31]). Запишем эти методы применительно к данному тесту с указанием формул моделирования.

Метод 1:

1) а/гпгтрпнпурм ттрттпр к- тто закону Пуассона с параметром Л ([0,Т]) =.

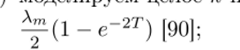
2) моделируем к точек {ъ}$₌₁ на [0, Т] независимо с плотностью.

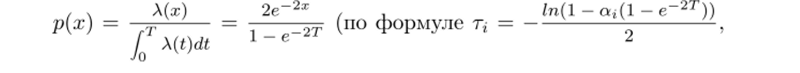
где а* независимые равномерно распределенные случайные величины на [0.1]);

3) упорядочим точки {rj}j_=l и полагаем ?(tj) = j.

В методе 2 и методе 3 полагаем Ао = А_т на всем интервале [0,Т].

Результаты статистического моделирования приведены на рис. 1.30 и в табл. 1.19. На рис. 1.30 приведены графики точного математического ожидания и оценка методом 1 на интервале [0,2] для, А = 0.6. Полученные оценки остальными методами не приведены ввиду сильного наложения графиков.

В табл. 1.19 приведены полученные абсолютные погрешности е оценки математического ожидания в последней точке и время счета t_C4 для различных параметров А. Из табл. 1.19 видно, что при малых интенсивностях (А < 1) все методы сравнимы по времени счета. При больших, А метод 1 считает быстрее других методов.

Тест 3. Стационарное решение задачи Коши.

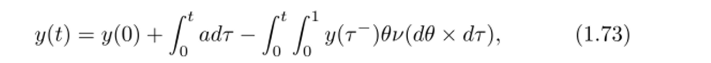
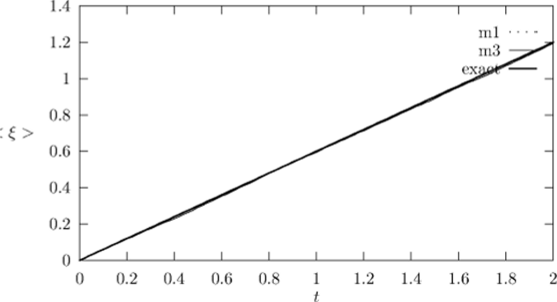
Рис. 1.29. Графики точного математического ожидания и полученных оценок (тест 1).

где пуассоновская мера v на [0,1] х R₊ задана мерой П(d, 0) = А (1 — 9)^Х~¹(Ю, является гамма-распределением с параметрами а, А, а плот;

При численном решении (1.73) параметры принимали следующие значения: а = 1, Л = 3. Начальное значение моделировалось как равномерная случайная величина на [0,1]. Численное решение в узлах сетки определялось по формуле.

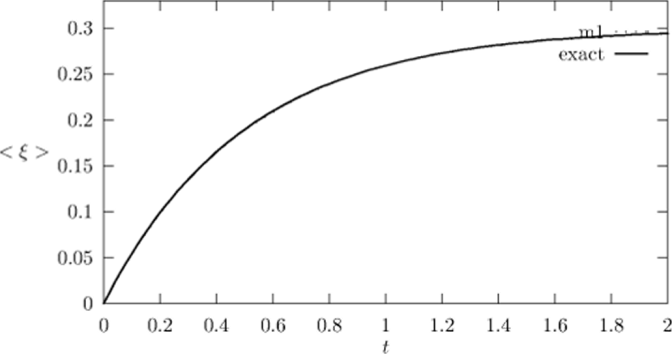
Рис. 1.30. График математического ожидания (тест 2).

ность распределения имеет вид р (х) = х^хехр (—х/а)/(а^х+1) [142]. Математическое ожидание решения имеет вид.

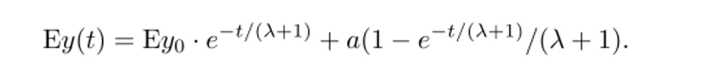
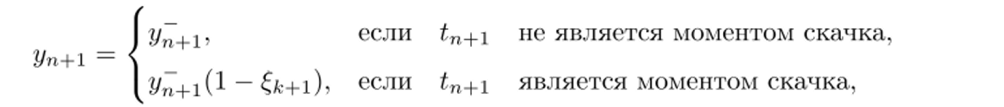
где у~_г = y_n+tk+1 —tk- Моделирование значений случайной величины с плотностью 3(1 — в)², в Е [0,1], осуществлялось по формуле = 1 — (ад,)¹/³, где a.k — равномерная случайная величина на Т = 10.

Моделирование пуассоновской меры осуществлялось методом 1 и методом 3.

Таблица 1.20. Погрешность оценки математического ожидания и время счета для разных интенсивностей (тест 3).

Результаты статистического моделирования приведены на рис. 1.31, 1.32 и в табл. 1.20. На рис. 1.31 приведены график плотности стационарного решения и гистограммы, полученные численным методом 1 при t = 5 и t = 20. На рис. 1.31 видно, что при t = 5 решение еще не является стационарным. На рис. 1.32 приведены графики точного математического ожидания и оценки, полученные методом 1. Графики, полученные методом 3, не приводятся, так как они визуально совпадают с графиками, полученными методом 1.

В табл. 1.20 приведены полученные абсолютные погрешности е оценки математического ожидания и время счета t_C4 при t = 5 и t = 20 (Л = 0.6).

Проведенные численные эксперименты демонстрируют возможность применения различных методов Монте-Карло для моделирования однородных и неоднородных пуассоновских ансамблей.

Проведем сравнение двух алгоритмов: метода «максимального сечения» (метод 3) и его модификации (метод За), рассмотренных в главе 3 пособия [31] и предназначенных для моделирования неоднородного пуассоновского процесса.

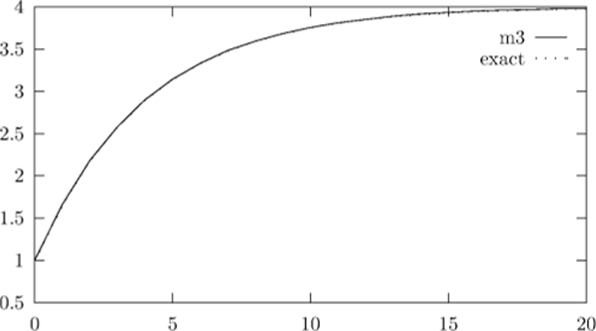
Рис. 1.32. График математического ожидания (тест 3).

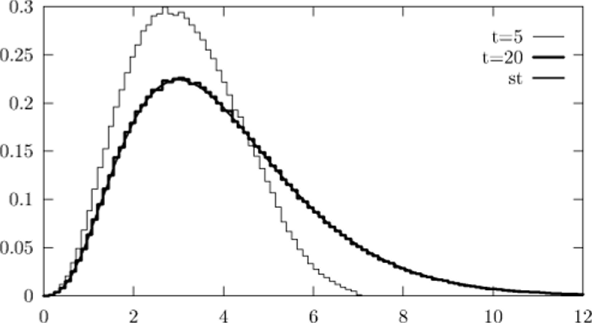
Рис. 1.31. График стационарной плотности и ее оценки при t = 5 и t = 20 (тест 3).

Для оценки математического ожидания численно моделируется N траекторий. При приближенном вычислении математического ожидания Е? случайной величины? с конечной дисперсией D? = о² по фор- 1 ^N

муле ?n = ^ПР^И заданном уровне доверия (1 — е) имеет место г=1.

cooTiioiiieinie.

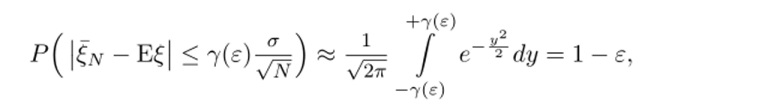
где 7(г) — константа, определяемая выбором величины е. При е = 0.003 имеем 'у (е) = 3, а при е = 0.3 получаем 7(5) = 1.

В таблицах с результатами численных экспериментов приведены доверительные интервалы для оценки математического ожидания при 7 = 1.

Тест 4. Моделирование неоднородного пуассоновского процесса ?(?), t > 0 с интенсивностью А (?) = A_me^-2i и Е?(?) = -^(1 — е^-2*). Для оценки математического ожидания моделировалось N = 10^ъ траекторий на интервале [0, Т], Т = 2.

В методах 3 и За полагаем Ао(t) = A_w на всем интервале [0, Т]. Результаты статистического моделирования приведены ниже. В таблицах указаны полученные абсолютные погрешности е оценки математического ожидания в последней точке и время счета t_C4 для различных пара;

метров А_ш. В табл. 1.21 приведены результаты расчетов при использовании «генератора» псевдослучайных чисел RAND [911 (с модулем 2⁴⁰ и множителем 5¹⁷), а в табл. 1.22 для «генератора» псевдослучайных чисел RND128 [202] (с модулем 2¹²⁸ и множителем 5^100 109).

Результаты численного моделирования демонстрируют уменьшение трудоемкости вычислений при использовании метода За вместо метода 3. Из таблиц видно, что оценки, полученные обоими методами, попадают в доверительные интервалы, а время счета метода За меньше, чем время счета метода 3, более чем на 10%.

Статистическое соответствие оценок, полученных алгоритмами 3 и За (с использованием теоремы 1 и без нее), является дополнительным критерием удовлетворительности используемых «генераторов» псевдослучайных чисел RAND и RND128.