Построение кривой нормального распределения по опытным данным. 
Проверка гипотезы о нормальном распределении выборки

Цель работы: овладение студентом способами построения эмпирической и теоретической (нормальной) кривой распределения; выработка умения и навыков применения критериев согласия для проверки выдвинутой статистической гипотезы.

Содержание работы: на основе дискретного вариационного ряда, полученного в лабораторной работе № 1, выполнить следующее:

• 1. Построить эмпирическую (полигон) и теоретическую (нормальную) кривую распределения.
• 2. Проверить согласованность эмпирического распределения с теоретическим нормальным, применяя три критерия:
  • а) критерий Пирсона;
  • б) один из критериев: Колмогорова, Романовского, Ястремского;
  • в) приближенный критерий.

Методика выполнения работы Продолжим вероятностно-статистическую обработку результатов эксперимента, предложенных в лабораторной работе № 1, то есть число рабочих дней без простоя. За основу берем дискретный вариационный ряд в табл.

и значения и .

Эмпирическая кривая распределения представляет собой полигон частот (см. лабораторную работу № 1). Для построения теоретической (нормальной) кривой найдем координаты точек, для чего рассчитаем теоретические частоты (табл.).

ni.
247,5.		— 13.	— 3,642.	0,53.	0,7 875 966.
250,5.		— 10.	— 2,819.	0,751.	1,125 948 282.
253,5.		— 7.	— 1,995.	0,5 452.	8,170 837 687.
256,5.		— 4.	— 1,172.	0,20 084.	30,987 358.
259,5.		— 1.	— 0,348.	0,37 555.	56,28 121 406.
262,5.			0,475.	0,35 646.	53,42 102 176.
265,5.			1,298.	0,17 175.	25,73 916 502.
268,5.			2,122.	0,4 201.	6,295 210 389.
271,5.			2,945.	0,522.	0,781 555 052.

Строим эмпирическую и теоретическую кривые (рис.).

дискретный вариационный статистика выборка.

Рис. 1 Эмпирическая и теоретическая кривые

Проверим согласованность эмпирического распределения (число рабочих дней без простоя) с теоретическим нормальным по критерию Пирсона. Вычислим величину по формуле:

.

Для нахождения суммы составляем расчетную табл.

		— 3.		1,125.
		— 9.		2,7.
				7,875.
		— 8.		1,20 754 717.
		— 5.		0,961 538 462.
				1,5.

Находим число степеней свободы.

.

Выбираем уровень значимости. По таблице критических точек распределения (приложение 5) находим. Так как, то делаем вывод, что данные выборки, характеризующие число рабочих дней без простоя, не подчиняются нормальному закону распределения.

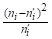
Проведём проверку близости эмпирического распределения к нормальному по критерию Романовского. Вычислим, согласно (32), величину. Так как, , то, т. е. расхождение между эмпирическим и теоретическим распределением несущественно, что позволяет утверждать, что данные выборки, характеризующие число рабочих дней без простоя по критерию Романовского подчиняются нормальному закону распределения. К такому же выводу мы приходим, применяя критерий Колмогорова.

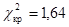
Наконец, проведём проверку близости рассматриваемой выборки к нормальному распределению по приближенному критерию, используя выборочные статистики: асимметрию, эксцесс и их средние квадратические отклонения. В лабораторной работе № 1 были найдены. Средние квадратические отклонения для асимметрии и эксцесса находим по формулам.

.

.

Так как.

и.

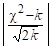
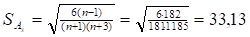
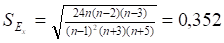
то делаем вывод, что данные выборки, характеризующие число рабочих дней без простоя, не подчиняются нормальному закону распределения.

Итак, для проверки согласованности эмпирического распределения с теоретическим нормальным мы применили 4 критерия, два из них подтвердили близость выборочной совокупности к нормальному распределению. Однако, учитывая, что критерий Колмогорова является более мощным, чем критерий 2 Пирсона, и подтверждает близость рассматриваемой выборки к нормальному распределению, окончательно заключаем, что за закон распределения признака Х — число рабочих дней без простоя — можно принять нормальное распределение.