Задание 6. Решение обыкновенных дифференциальных уравнений

Постановка задачи

• 1. Рассмотрите задачу, состоящую в поиске решения обыкновенного дифференциального уравнения для t от t₀ до t_k с шагом? t при начальном условии y (t₀)=y₀ (задачу Коши). Выясните возможность аналитического решения задачи.
• 2. Разработайте программу на С для решения поставленной задачи модифицированным методом Эйлераи методом Рунге-Куттыс фиксированным шагом? t (значение? t возьмите равным десятой доле интервала интегрирования).

Математическая постановка задачи

В инженерной практике довольно часто приходится встречаться с обыкновенными дифференциальными уравнениями при решении различных прикладных задач. Обыкновенным дифференциальным уравнением называется выражение вида.

F (X, Y, Y', Y",…, Y^n-1, Yⁿ) = 0, (1).

где Х — независимая переменная;

Y — искомая функция от Х;

Y', Y",…, Yⁿ -производные порядка 1,2,…, n.

Порядок старшей производной, входящей в уравнение (1), называется порядком дифференциального уравнения.

Простейшим обыкновенным дифференциальным уравнением является уравнение 1-го порядка.

y'= f (x, y) (2).

Основная задача, относящаяся к этому уравнению, есть задача Коши: найти решение дифференциального уравнения (2) в виде у=у (х), удовлетворяющее начальному условию Y (Xo)=Yo, т. е. требуется найти интегральную кривую у=у (х), проходящую через заданную точку М (Хо, Yo).

Для нахождения решения дифференциального уравнения (1) необходимо задать такое количество начальных условий, какое соответствует порядку старшей производной, а именно задать значения.

Yo=Y (Xo); Yo'=Y'(Xo),…, Y₀^n-1 = Y^n-1 (Xo) (3).

Уравнение (1) называется разрешенным относительно старшей производной, если оно имеет вид.

Y⁽ⁿ⁾ =f (X, Y, Y', Y",…, Y^n-1) (4).

Если дифференциальное уравнение (1) разрешимо относительно старшей производной, то его можно свести к системе обыкновенных дифференциальных уравнений 1-го порядка заменой на неизвестную функцию Р₁(х), у" на Р₂(х) и т. д.

Таким образом, имеем.

y'=P₁,.

P1'=P₂,.

P2'=P₃,.

P’n-1 = f (x, y, P₁, P₂,…, P_n-1), причем.

Y (Xo)=Yo.

P₁(Xo)=Yo'.

P₂(Xo)=Yo".

.. .. .. .. .

P _n-1(Xo)=Yo^n-1 .

При решении инженерных задач чаще всего приходится иметь дело с уравнениями, общее решение которых не выражается в аналитическом виде. Поэтому возникает необходимость применять те или иные методы, дающие приближенное решение задачи.

6.3 Описание методов решения

Метод Эйлера для расчета дифференциальных уравнений имеет небольшую точность расчета. Точность расчета у него зависит от размера шага линейно, зависимость точности от шага — первой степени. То есть, чтобы увеличить точность в 10 раз, надо уменьшить шаг в 10 раз. Этот метод является сравнительно грубым и применяется в основном для ориентировочных расчетов.

Метод численного решения дифференциального уравнения 1-го порядка y'= f (x, y) с начальным условием Y (Xo)=Yo основан на разложении решения в ряд Тейлора в h-окрестности точки Хо:

Y1 = Y (x+h) = Y (Xo) + h*Y'(Xo) + (h²/2)*Y"(Xo) +…

При отбрасывании всех членов ряда, содержащих производные 2-го и высших порядков, получим.

Y1 = Yo + h*f (Xo, Yo), где f (x, y) — правая часть уравнения y'= f (x, y) .

Пользуясь значением Y1 из разложения y (x) в hокрестности точки.

Х1=Хо+h, получим.

Y2=Y1+h*f (X1,Y1),.

аналогично продолжая для следующей Х i+1 точки, получим.

Y _i+1 = Y_i+h*f (Xi, Yi).

Если дано уравнение 2-го порядка Y'=f (x, y, y') c начальными условиями Y (Xo)=Yo и Y'(Xo)=Yo', то такое уравнение можно свести к системе двух уравнений 1-го порядка.

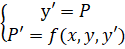
причем.

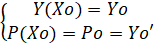
Тогда приближенные значения функций у и Р в точке можно вычислить.

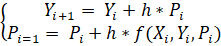
где f (X_i, Y_i, P_i) — правая часть уравнения Y'=f (x, y, y').

При достаточно малой величине шага h метод Эйлера дает решение с большой точностью, т.к. погрешность решения близка к h².

Модифицированный метод Эйлера имеет точность второго порядка. В методе Эйлера производная берется в начале шага и по ней прогнозируется движение системы на конец шага, считая, что во время шага производная неизменна. То есть в течение всего шага производная считается той, какой она была в самом начале шага. Это основной источник неточности.

Улучшение метода Эйлера состоит в том, что берется производная не в начале шага, а как промежуточное или среднее на разных участках одного шага. В разных вариантах метода вычисляют несколько производных в разных частях шага и усредняют их. Конечно, в этом случае число вычислений увеличивается, — но не в десятки раз, — а вот точность возрастает на порядок, в этом и состоит выигрыш.

Модифицированный метод Эйлера второго порядка реализуется следующими рекуррентными формулами:

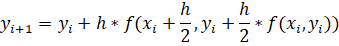
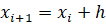
Данная схема называется еще методом предиктор — корректор (предсказывающее — исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.

Метод дает погрешность порядка h³ и имеет меньшее время вычислений, поскольку вместо нескольких итераций производится вычисление только одного значения.

.

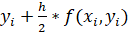
Метод Рунге-Кутта четвертого порядка для численного решения дифференциальных уравнений первого порядка По сравнению с описанным выше методом Эйлера метод Рунге-Кутта имеет более высокую точность. Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. В методе Рунге-Кутта четвертого порядка вычисления производятся по формулам:

K₁=h*F (X_i, Y_i);

K₂=h*F (X_i+h/2,Y_i+K₁/2);

K₃=h*F (X_i+h/2,Y_i+K₂/2);

K₄=h*F (X_i+h, Y_i+K₃);

Y_i+1 = Y_i + (K₁+2*K₂+2*K₃+K₄) / 6.

Метод Рунге-Кутта применим также для приближенного решения систем ОДУ, применяя формулы для каждого уравнения в отдельности. При этом погрешность интегрирования есть величина порядка h⁵.

В данном задании необходимо задать: шаг h и начальные условия (t₀, t_k, y₀).

Выходными данными являються: количество итераций, решение ДУ на каждом шаге итераций, решение ДУ.