Движение заряженной частицы в квазиплоской электромагнитной волне

О различных способах представления неплоской волны

Известно, что хорошо заданный вопрос содержит половину ответа. В этом нередко можно убедиться в различных задачах математической физики, когда заранее предполагается форма решения дифференциального уравнения, и лишь затем по ней отыскивается ответ. В каждом ответе к задаче можно увидеть влияние стартовых величин. Это относится и к задаче о движении частицы во внешних полях. Например, в представлении поля пользуются разложением по малому безразмерному параметру и вводят безразмерные параметры [60]-[61].

Попробуем ввести векторный потенциал электромагнитного поля, зависящий от некоторых безразмерных (в пределах п. 3.2.1) пространственных координат и и координаты как ряд Тейлора:

(3.23).

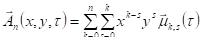
(3.24).

где — остаточный член в форме Лагранжа, и частные производные от некоторой функции.

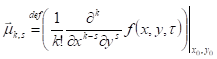
(3.25).

Из (3.24) с учетом (2.2) и (2.4) электрическое и магнитное поля равны:

.

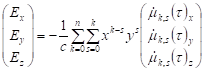
(3.26).

где () обозначает соответствующую j-ую компоненту. Легко увидеть, что формально.

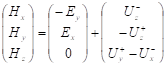
(3.27).

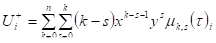
где остатки и равны друг другу только в первом приближении n=1. Уже при n=2:

.

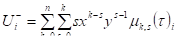
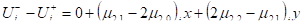
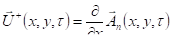
Между прочим, можно заметить, что, .

Минимальный учет пространственной неоднородности по и возможен при n=1:

.

.

.

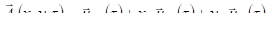
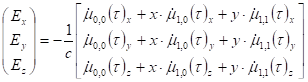
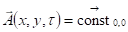
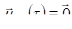
Логично предположить, что при осевой симметрии (относительно z). Видеть, чем сложен случай неплоской электромагнитной волны, можно хотя бы по тому, что для плоской электромагнитной волны все компоненты, обведённые сейчас серой пунктирной рамкой, были тогда равны нулю. Из (3.26) и (3.24) следует, что электрическое поле в пространстве отсутствует тогда, когда векторное поле стационарно по величине, т. е. не меняется как по времени, так и по координате, а отсутствие магнитного поля (вихрь векторного поля (3.24) тождественно равен нулю) автоматически требует обнуления всех частных производных по и, начиная с первых и. Следовательно, нулевому полю отвечает вектор констант. Согласно (3.26) постоянному электрическому полю, направленному вдоль оси, должно отвечать векторное поле с, , ().

Векторное поле (3.24) можно переписать в матричной форме, расцепив x и y,.

.

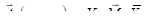
где матрица над полем 3-компонентных векторов равна.

, , ,.

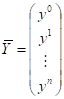
т.е. все элементы под побочной диагональю матрицы равны. Разложение векторного поля в ряд Тейлора не по двум переменным (3.24), а по трём должно приводить уже не к матричной, а тензорной записи с тензором третьего ранга над полем 3-компонентных векторов .

Введём теперь векторное поле с явным осциллирующим множителем:

Электрическое и магнитное поля равны.

.

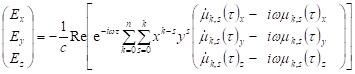
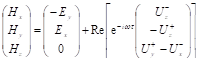
. (3.29).

Формально запись (3.28) отличается от (3.24) только умножением на экспоненту и взятием действительной части, но в действительности эти два дополнительных действия приводят к появлению новых слагаемых в электрическом поле, обведённых синей пунктирной рамкой.

При n=1 из (3.28) и (2.2), с учетом (2.4), получаем.

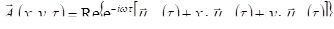
(3.30).

.

.

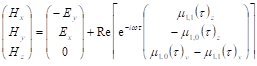
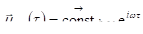
Из (3.29) можно вычислить значения частных производных, при которых электрическое поле равно нулю,. Чтобы магнитное поле также равнялось нулю, требуется, как и ранее, ().

Если не зависят от, то из (3.30).

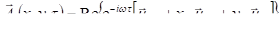
(3.31).

и параксиальное приближение (3.31) дает выражения для частных производных:

, ().

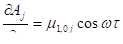
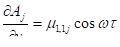
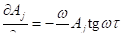
Для электромагнитной волны можно задавать напрямую выражения напряжённостей электрического и магнитного поля, минуя векторный потенциал. Будем следовать в этом работе [52]. При этом теперь будем полагать, и размерными:

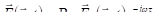
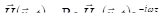
. (3.33).

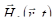
Если и постоянны, то (3.33) задаёт монохроматическую плоскую волну, бегущую вдоль оси z. В немонохроматической волне и меняются во времени и пространстве. Пусть ф_b и l_b — такие время и длина, на которых функции и существенно изменяются, но при и меняются всё же медленно в сравнении с комплексной экспонентой. Аналогично (2.47) можно ввести параметры, которые удовлетворяют сильным неравенствам:

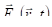
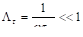
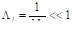
, (3.34).

где. Поле (3.33) при выполнении (3.34) называется квазимонохроматической квазиплоской электромагнитной волной. Когда, электромагнитную волну на интервале удобно считать монохроматической квазиплоской волной. Когда, её удобно считать плоской квазимонохроматической волной в области с поперечными размерами к направлению распространения.

Подстановка (3.33) в уравнения Максвелла с вычислениями в первом порядке по малым параметрам (3.34) даёт выражения для компонент и :

,.

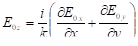
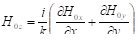
, (3.35).

где произвольные и меняются медленно, так что их старшие производные высших порядков пренебрежимо малы. Учитывая (3.33):

.

.

.

(3.36).

где, ,, .

Видно, что между (3.33) и (3.29) существует глубокая связь, особенно если пренебречь суммами и .