Основные понятия относящиеся к механическим колебаниям и волнам

Многообразные движения тел в окружающем нас мире можно разделить на два класса в зависимости от того, остается ли тело в процессе движения вблизи некоторого среднего положения или такого положения нет. Мы обратимся к первому классу. Отличительной чертой многих движений рассматриваемого класса является их периодичность, т. е. повторяемость через определенные интервалы времени.

Движения, которые точно или приблизительно повторяются через одинаковые промежутки времени, называются механическими колебаниями.

Колебания бывают разные. Одни колебания, как, например, в швейной машине, способны совершаться только тогда, когда на тело действуют периодически изменяющиеся внешние силы, которые и вынуждают тело совершать колебательное движение. Такие колебания называют вынужденными. Другие же колебания обусловлены действием внутренних сил и потому способны происходить сами по себе. Таковы, например, колебания грузика на пружине, возникающие после того, как грузик сместили из положения равновесия и отпустили.

Колебания, происходящие под действием внутренних сил и возникающие в системе после того, как система была выведена из состояния равновесия и предоставлена самой себе, называются свободными.

К свободным колебаниям относятся: колебания груза на пружине, а также груза на нити (маятника). Отличительной особенностью систем, в которых происходят свободные колебания, является наличие у них положения устойчивого равновесия. Именно около этих положений и совершаются свободные колебания.

Для того чтобы в той или иной системе возникли свободные колебания, необходимо выполнение следующих условий:

• 1. Системе должна быть сообщена избыточная энергия. Эту энергию можно сообщить системе либо в виде потенциальной энергии, либо в виде кинетической энергии, либо в виде и той и другой.
• 2. Избыточная энергия, сообщенная системе, не должна в процессе возникшего движения полностью тратиться на преодоление трения.

Эти два условия являются необходимыми, но не достаточными для существования свободных колебаний. Система, помимо этого, должна обладать еще некоторыми определенными свойствами, которые могут послужить причиной возникновения в системе колебаний.

Основные кинематические характеристики колебаний:

• 1) амплитуда колебаний (А) — это максимальное расстояние, на которое удаляется колеблющееся тело от своего положения равновесия. Амплитуда свободных колебаний определяется начальными условиями, измеряется амплитуда в метрах;
• 2) период колебания (Т) — это минимальный промежуток времени, по истечении которого система возвращается в прежнее состояние; иначе говоря, период колебания — это время, за которое совершается одно полное колебание;
• 3) частота колебаний (х) — это число колебаний, совершаемых за 1 с, измеряется в герцах (Гц);
• 4) циклическая частота (w) — это величина, в 2р раз большая частоты.

Физический смысл циклической частоты заключается в том, что она показывает, какое число колебаний совершается за 2р секунд. Измеряется циклическая частота в, или с-1.

Для периода, частоты и циклической частоты справедлива формулы:

;; ,.

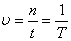
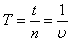
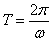
где п — число колебаний, а t — время, за которое произошло п колебаний.

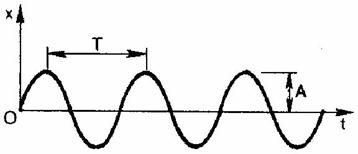
В процессе свободных колебаний положение колеблющегося тела непрерывно изменяется. Если трение настолько мало, что им можно пренебречь, то графиком зависимости координаты колеблющегося тела (материальной точки) от времени является синусоидальная кривая, или, кратко, синусоида.

График зависимости координаты колеблющегося тела от времени называют графиком колебаний. По графику колебаний легко определяются все кинематические характеристики колебательного движения.

Колебания, при которых координата колеблющегося тела меняется с течением времени по закону синуса (или косинуса), называются гармоническими.

Если момент начала отсчета времени колебаний совпадает с моментом максимального отклонения маятника от положения равновесия, уравнение колебаний будет:

или ,.

т. е. колебания будут синусоидальными и происходить без начальной фазы б0. х — смещение маятника.

Если момент начала отсчета времени колебаний не совпадает ни с моментом максимального отклонения от положения равновесия, ни с моментом прохождения им положения равновесия, то колебания происходят с начальной фазой и уравнение таких колебаний имеет вид:

или .

Фаза колебаний б — это величина, которая позволяет определить, какая доля периода прошла с момента начала колебаний и наиболее полно характеризует колебательный процесс:

.

Задачи механических колебаний можно условно разделить на четыре группы: задачи на уравнения гармонических колебаний, задачи о колебаниях пружинного маятника, задачи о колебаниях математического маятника и задачи о колебаниях физического маятника — маятника произвольной формы, к колебаниям которого нельзя применять формулы, применимые к колебаниям пружинного или математического маятников.

Пружинный маятник Колебательная система в этом случае представляет собой совокупность некоторого тела и прикрепленной к нему пружины. Пружина может располагаться либо вертикально (вертикальный пружинный маятник), либо горизонтально (горизонтальный пружинный маятник).

.

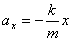
где ах — ускорение, т — масса, х — смещение пружины, k — жесткость пружины.

Это уравнение называют уравнением свободных колебаний пружинного маятника.

Оно правильно описывает рассматриваемые колебания лишь тогда, когда выполнены следующие предположения:

• 1)силы трения, действующие на тело, пренебрежимо малы и поэтому их можно не учитывать;
• 2) деформации пружины в процессе колебаний тела невелики, так что можно их считать упругими и в соответствии с этим пользоваться законом Гука.

Свободные колебания пружинного маятника имеют следующие причины.

• 1. Действие на тело силы упругости, пропорциональной смещению тела х от положения равновесия и направленной всегда к этому положению.
• 2. Инертность колеблющегося тела, благодаря которой оно не останавливается в положении равновесия (когда сила упругости обращается в нуль), а продолжает двигаться в прежнем направлении.

Выражение для циклической частоты имеет вид:

.

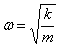
где w — циклическая частота, k — жесткость пружины, т — масса.

Эта формула показывает, что частота свободных колебаний не зависит от начальных условий и полностью определяется собственными характеристиками самой колебательной системы — в данном случае жесткостью k и массой т.

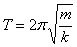
Это выражение определяет период свободных колебаний пружинного маятника.

Математический маятник Математический маятник — это материальная точка, подвешенная на невесомой и нерастяжимой нити, находящейся в поле тяжести Земли. Математический маятник — это идеализированная модель, правильно описывающая реальный маятник лишь при определенных условиях. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.

Колебательную систему в данном случае образуют нить, присоединенное к ней тело и Земля, без которой эта система не могла бы служить маятником.

.

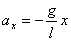
где ах — ускорение, g — ускорение свободного падения, х — смещение, l — длина нити маятника.

Это уравнение называется уравнением свободных колебаний математического маятника. Оно правильно описывает рассматриваемые колебания лишь тогда, когда выполнены следующие предположения:

• 1) будем считать, что силы трения, действующие на тело, пренебрежимо малы и потому, их можно не учитывать;
• 2) рассматриваются лишь малые колебания маятника с небольшим углом размаха.

Свободные колебания любых систем во всех случаях описываются аналогичными уравнениями.

Причинами свободных колебаний математического маятника являются:

• 1. Действие на маятник силы натяжения и силы тяжести, препятствующей его смещению из положения равновесия и заставляющей его снова опускаться.
• 2. Инертность маятника, благодаря которой он, сохраняя свою скорость, не останавливается в положении равновесия, а проходит через него дальше.

Период свободных колебаний математического маятника.

.

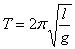
Период свободных колебаний математического маятника не зависит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.

Превращение энергии при гармонических колебаниях При гармонических колебаниях пружинного маятника происходят превращения потенциальной энергии упруго деформированного тела.

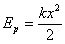
в его кинетическую энергию.

.

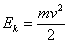
где k — коэффициент упругости, х — модуль смещения маятника из положения равновесия, m — масса маятника, v — его скорость. В соответствии с уравнением гармонических колебаний:

.

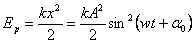
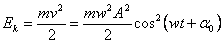
Полная энергия пружинного маятника:

.

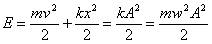
Полная энергия для математического маятника:

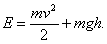
В случае математического маятника.

Превращения энергии при колебаниях пружинного маятника происходи в соответствии с законом сохранения механической энергии.

.

При движении маятника вниз или вверх от положения равновесия его потенциальная энергия увеличивается, а кинетическая — уменьшается. Когда маятник проходит положение равновесия (х = 0), его потенциальная энергия равна нулю и кинетическая энергия маятника имеет наибольшее значение, равное его полной энергии.

Таким образом, в процессе свободных колебаний маятника его потенциальная энергия превращается в кинетическую, кинетическая в потенциальную, потенциальная затем снова в кинетическую и т. д. Но полная механическая энергия при этом остается неизменной.

Вынужденные колебания. Резонанс.

Колебания, происходящие под действием внешней периодической силы, называются вынужденными колебаниями. Внешняя периодическая сила, называемая вынуждающей, сообщает колебательной системе дополнительную энергию, которая идет на восполнение энергетических потерь, происходящих из-за трения. Если вынуждающая сила изменяется во времени по закону синуса или косинуса, то вынужденные колебания будут гармоническими и незатухающими.

В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из состояния равновесия), в случае вынужденных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на преодоление трения, и потому полная энергия колебательной системы no-прежнему остается неизменной.

Частота вынужденных колебаний равна частоте вынуждающей силы. В случае, когда частота вынуждающей силы х совпадает с собственной частотой колебательной системы х0, происходит резкое возрастание амплитуды вынужденных колебаний — резонанс. Резонанс возникает из-за того, что при х = х0 внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. График зависимости амплитуды вынужденных колебаний Ат от частоты вынуждающей силы х представлен на рисунке, этот график называется резонансной кривой:

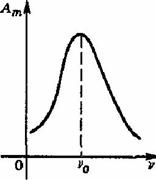
Явление резонанса играет большую роль в ряде природных, научных и производственных процессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены.

Механические волны.

Еще одним видом движения являются волны. Отличительной особенностью этого движения, делающей его уникальным, является то, что в волне распространяются не сами частицы вещества, а изменения в их состоянии (возмущения).

Среда называется упругой, если между ее частицами существуют взаимодействия, препятствующие какой-либо деформации этой среды.

Если какое-либо тело совершает колебания в упругой среде, то оно воздействует на частицы среды, прилегающие к телу, и заставляет их совершать вынужденные колебания. Среда вблизи колеблющегося тела деформируется и в ней возникают упругие силы. Эти силы действуют на все более удаленные от тела частицы среды, выводя их из положения равновесия. Постепенно все частицы среды вовлекаются в колебательное движение.

Волнами называются всякие возмущения состояния вещества или поля, распространяющиеся в пространстве с течением времени.

Упругими волнами называются механические возмущения (деформации), которые распространяются в упругой среде. Тела, вызывающие эти возмущения в среде, называются источниками волн. Упругие волны называются звуковыми или акустическими, если соответствующие им механические деформации среды имеют малые амплитуды.

Отличие упругих волн в среде от любого другого упорядоченного движения ее частиц состоит в том, что распространение волн не связано с переносом вещества среды из одного места в другое на большие расстояния.

Волновой поверхностью (фронтом волны) называется совокупность точек среды, колеблющихся в одинаковых фазах. На волновой поверхности фазы колебаний различных точек в рассматриваемый момент времени имеют одно и то же значение.

Лучом называется линия, касательная к которой в каждой точке совпадает с направлением распространения волны. В однородной изотропной среде луч является прямой, перпендикулярной к фронту волны, и совпадает с направлением переноса энергии волны.

В плоской волне волновыми поверхностями являются плоскости, перпендикулярные к направлению распространения волны. Лучами являются параллельные прямые, совпадающие с направлением скорости распространения волны. Такие волны могут быть получены на поверхности воды с помощью колебаний плоского стержня.

Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны.

Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.

В газах и жидкостях, которые не обладают упругостью формы, распространение поперечных волн невозможно. В твердых телах возможно распространение как продольных, так и поперечных волн, связанных с наличием упругости формы.

Каждая волна распространяется с некоторой скоростью. Под скоростью волны понимают скорость распространения возмущения.

Скорость волны определяется свойствами среды, в которой эта волна распространяется. В твердых телах скорость продольных волн больше скорости поперечных. Это обстоятельство учитывается для определения местоположения очагов землетрясения.

Землетрясения являются источниками так называемых сейсмических волн, распространяющихся в земной коре в виде как продольных, так и поперечных волн. Первыми на регистрирующую станцию приходят продольные волны, затем поперечные.

Одной из важнейших характеристик любой волны является длина волны.

Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебания в ее источнике. Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне.

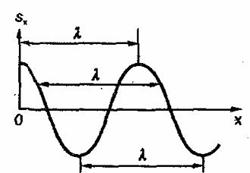
Длина волны обозначается греческой буквой л (ламбда). Единицей измерения является метр. Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, длина волны.

.

Длина волны совпадает с расстоянием между двумя ближайшими гребнями (или впадинами) волны и зависит как от свойств среды (через скорость v), так и от свойств источника волны (через период его колебания Т).

Связь скорости волны с ее частотой:

.

здесь — частота колебаний.

При переходе волны из одной среды в другую изменяются скорость и длина волны, а циклическая частота, период и частота при этом не изменяются.

Если частицы среды совершают гармонические колебания, то в этой среде распространяется гармоническая волна. Уравнение бегущей гармонической волны.

или ,.

а отраженной.

и .

Здесь х — смещение частиц среды, А — амплитуда их колебаний, щ — циклическая частота колебаний частиц, t — время колебаний частиц, равное времени распространения волнового процесса в среде, k — волновое число, у — координата фронта волны, б0, -начальная фаза колебаний частиц, б — фаза колебаний.

Циклическую частоту щ и волновое число k можно определить так:

, .

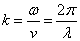
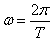
Звук.

Звуковые волны с частотами от 16 до 20 000 Гц воздействуют на органы слуха человека, вызывают слуховые ощущения и называются слышимыми звуками. Звуковые волны с частотами менее 16 Гц называются инфразвуками, а с частотами более 20 000 Гц — ультразвуками.

Шумами называются звуки, образующие набор частот, непрерывно заполняющих некоторый интервал.

Музыкальные звуки обладают линейчатым спектром частот; им соответствуют периодические или почти периодические колебания. Каждая синусоидальная звуковая волна называется тоном. Высота тона зависит от частоты: чем больше частота, тем выше тон.

Громкость звука зависит от интенсивности звука, т. е. определяется амплитудой колебаний в звуковой волне. Наибольшей чувствительностью органы слуха обладают к звукам с частотами от 700 до 6000 Гц.

Порогом слышимости называется наименьшая интенсивность звуковой волны, которая может быть воспринята органами слуха. Стандартный порог слышимости принимается равным 10−12Вт/м2 при частоте l кГц.

Как и всякая волна, звуковая волна характеризуется скоростью распространения колебаний в ней. С длиной волны л, и частотой колебаний х скорость v связана формулой:

.

Скорость звука различна в различных средах.