Осцилляция решений нелинейного дифференциально-разностного уравнения с конечными разностями p-произвольного нечетного порядков с эллиптическим оператором

Быков Я.В. изучил осцилляционные свойства решений различных классов линейных, нелинейных, интегро-разностных и интегро-дифференциально-разностных уравнений с конечными разностями первого порядка. С Я. В. Быковым и Б. К. Темировым ранее были установлены достаточные условия осциллируемости решений операторно-разностных уравнений с конечными разностями второго, четвертого и произвольного m-четного порядков.

Вопрос осцилляции решений уравнений нелинейных дифференциально-разностных уравнений с конечными разностями m-нечетного порядков с с эллиптическим оператором ранее не изучался.

В данной статье устанавливается достаточное условие осцилляции решений нелинейного дифференциально-разностного уравнения с конечными разностями pпроизвольного нечетного порядков с эллиптическим оператором. Рассмотрим уравнения вида.

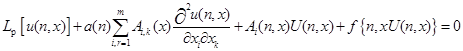
(1).

где: p — произвольное нечетное число.

Введем обозначения:

.

В уравнении (1) рассмотрена когда как заданные функции. В дальнейшем будем исходить из определений данной в работе [1].

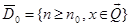
Определение 1. Всякую функцию, определенную в области называют правильной.

Определение 2. Правильную функцию называют положительной {отрицательной}, еслитакое, что Определение 3. Правильную функцию называют С — неосциллирующей, если она либо не положительна, либо не отрицательно. В противном случае ее называют С — осциллирующей.

Всюду предполагается: 1) — открытая ограниченная область с кусочно-гладкой границей; 2) n-натуральное число; 3); 4) непрерывные функции подля каждого фиксированного натурального числа; 5) заданная функция натурального аргумента. 6).

— эллиптический оператор и предполагается, что а) для любого набора вещественных чисел .

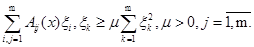
б).

достаточно гладкие функции (т. е. достаточно предполагать, чтобы эти функции имели частные производные второго порядка, удовлетворяющие в замкнутой области некоторому условию Гельдера).

7).

Осцилляция решений нелинейного дифференциально-разностного уравнения с конечными разностями различного порядка исследованы: 1го порядка в [1], 2го, 4го и произвольного четного порядков в [3] и 3го, 5го порядков в [5; 6]. c эллиптическими операторами. Известно [4], что все собственные значения краевой задачи.

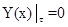
(2).

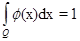
положительны, наименьшему собственному значению соответствует единственная нормированная собственная функция, (Нормированная в смысле). Если область параллелепипед, то.

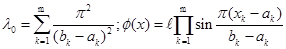
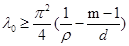
Если Q — выпуклая область, то где pрадиус наибольшего шара, вписанного в область Q. d- диаметр область Q: m — размерность область Q. Приведем следствие формулы Грина.

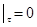
Следствие 1. Для всякой дважды непрерывно дифференцируемой функции (Символ означает, что) выполняется осцилляционный уравнение линейный.

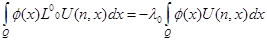
Следствие 2. Для всякой не отрицательной дважды непрерывно дифференцируемой функции.

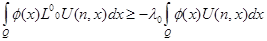
Теорема Иенсена. Пусть 1) f (z) — непрерывная выпуклая на (0, ?) функция (дважды дифференцируемая на (0, ?)), функция f (x) является выпуклой на этом интервале тогда и только тогда, когда 1) 2) Ф (х) непрерывная положительная функция, непрерывная по переменным группы х. Тогда имеет место неравенство.

Это соотношение называют неравенство Иенсена. Доказательство теоремы приведены в работе [2].

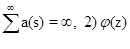
Лемма 1. Пусть 1) — неубывающая функция.

3) p-четное число. Тогда неравенство н.

(3).

не имеет положительного решения.

Доказательство. Допустим, что неравенство (3) имеет положительное решение, Тогда, поэтому -незрастающая функция. Следовательно, логически возможны только следующие допущения: 1) либо такое, что; 2) либо. Рассмотрим первый случай. Докажем, что это предположение противоречит неравенству. Отсюда.

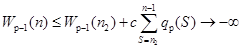
при.

Отсюда следует, что. Продолжая рассуждать аналогично почти также как и выше получим, что, что.

.

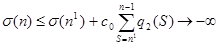
Далее суммируя это неравенство от получили при. Это соотношение противоречить неравенству .

Поэтому, первое предположение несостоятельны. Рассмотрим, второй случай.

• -неубывающая функция. Тогда логически возможны только следующие допущения:
  • 1. либо такое, что
  • 2. либо

Рассмотрим первый случай либо.

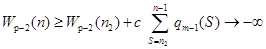
при Следовательно,. Продолжая такие же рассуждения, получим, чтотакие, что Тогда. С учетом этого неравенства из (3) имеем.

.

Учитывая следующее неравенство получим, что последнее неравенство противоречит условию леммы, поэтому, верно предположение.

• 1. противоречит условиям леммы. Поэтому, верно предположение
• 2. что

.

— невозрастающая функция. Логически возможны только следующие предположения: 1) либо такое, что.

2) либо. Первое предположение противоречит неравенству, что. Следовательно,. Производя аналогичные рассуждения получим, что. Отсюда вытекает, что с учетом этого неравенства из неравенств (2) имеем c=?

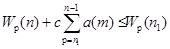
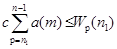
Суммируя неравенство от до получим. Так как, то усиливая неравенство получим, которое противоречит условию 1) леммы.

Замечание 1. Если выполнены условия 2), 3) леммы 1, а условия 1) не выполнены, то неравенство (3) может иметь положительное решение.

Замечание 2. Если 1) выполнены условия 1), 3) леммы 1; 2) p-нечетное число, то неравенство (3) может иметь положительное решение.

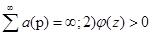
Лемма 2. Если 1) непрерывная неубывающая функция;

3) p — нечетное число, то для положительного решения неравенства (3) имеет место равенство.

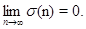
Доказательство. Предположим, что неравенство (3) имеет положительное решение.

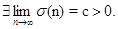
. Рассуждая почти также, как и при доказательстве леммы 1, показывается, что, 1) невозрастающая функция2) Допустим, что с?0. ТогдаС учетом этого, из неравенства (3) имеем. Так както это неравенство противоречит условию 1) леммы 2. Следовательно, предположение с?0 приводит к противоречию. Поэтому.

Скажем, что выполнено 1) условие если.

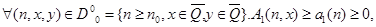
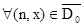
2) условие еслии.

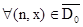
3) условиееслии.

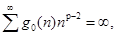
Теорема 1. Пусть 1) выполнены условия ,; 2) тогда каждое решение уравнения (1) либо осциллирует, либо.

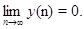
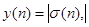
Доказательство. Допустим, что уравнение (1) имеет снеосциллирующее решение. Тогда неравенство имеет положительное решениечто противоречит теореме 1 из [5] и леммы 2. Следовательно, предположение существования Снеосциллирующего решения уравнения (1) приводят к противоречию. Поэтому либо решение С-осциллирует, либо.

Теорема 2. Пусть 1) выполнены условия ,.

2) ѓ.

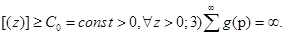
Тогда каждое решение уравнения (1) либо сосциллирует, либо.

Доказательство. Предположим, что уравнение (1) имеет снеосциллирующее решение. Тогда неравенство имеет положительное решение y (n).

Это утверждение противоречит условию 3) теоремы 2. Следовательно, предположение существования с — неосциллирующего решения уравнения (1) приводит к противоречию, поэтому решение либо с — осциллирует, либо.

Теорема 3. Пусть а) выполнены все условия теоремы 2) a (n)?0 Тогда все правильные решения уравнения (1) либо с — осциллирует, либо.

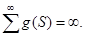
Теорема 4. Пусть 1) выполнены условия ,; 2) ц (z) — возрастающая непрерывная выпуклая на (0,?) функция; 3). Тогда каждое решение уравнения (1) либо с-осциллирует, либо Доказательство приводится аналогично к доказательству теоремы 3.

Теорема 5. Если а) выполнены все условия теоремы 4. b) a (n)?0, то все решения уравнения (1) либо осциллирует, либо.

• 1. Быков Я. В. Осцилляция решений операторно-разностных уравнений с конечными разностями первого порядка. — Фрунзе: Илим, 1985 — 263 с.
• 2. Быков Я. В., Темиров Б. К. Осцилляция решений операторно-разностных уравнений с конечными разностями второго, четвертого и произвольного четного порядков. — Фрунзе: Илим, 1990, — 124 с.
• 3. Быков Я. В., Мерзлякова Г. Д., Шевцов Е. И. Об осцилляторности решений нелинейных разностных уравнений // Дифференциальные уравнения. — 1975. — Т. 2, № 8. — C. 1460−1473.
• 4. Красносельский М. А. Положительные решения операторных уравнений. — М.: ГИФМЛ, 1962.
• 5. Темиров Б. К. Осцилляция решений нелинейного интегро-разностного уравнения с конечными разностями третьего порядка // Труды межд. конференции «Программные системы: теория и приложения» института программных систем РАН г. Переелавль-Залесский. 2006. С. 379−387.
• 6. Шарифова Т. О колеблемости решений некоторых разностных уравнений // Вопросы вычислительной и прикладной математики. — Ташкент, 1974. — Вып. 23. — С. 35−43.