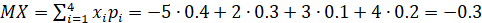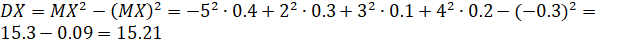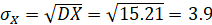Задание 3. Теория вероятностей

На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: п₁ с первого завода, n₂ со второго, n₃c третьего (табл. 3). Вероятность качественного изготовления изделий на первом заводе p₁на втором р₂, на третьем р₃. Какова вероятность того, что взятое случайным образом изделие будет качественным?

Решение.

n1= 25, n2=35, n3=40.

p1=0.9, p2=0.8, p3=0.7.

Задача на применение формулы полной вероятности.

Обозначим:

Н₁ — это событие, состоящее в том, что наугад взятое комплектующее изготовлено на первом заводе;

Н₂ — это событие, состоящее в том, что наугад взятое комплектующее изготовлено на втором заводе;

Н₃ — это событие, состоящее в том, что наугад взятое комплектующее изготовлено на третьем заводе.

Н₁, Н₂ и Н₃ — гипотезы; образуют полную группу событий.

По условию задачи априорные вероятности гипотез:

P (H₁)= 25/(25+35+40) = 0,25.

P (H₂)= 35/(25+35+40) = 0,35.

P (H₃)= 40/(25+35+40) = 0,40.

Обозначим, А — событие, состоящее в том, что взятое случайным образом изделие качественное.

Условные вероятности:

P (A|H₁)=0,9.

P (A|H₂)=0,8.

P (A|H₃)=0,7.

Тогда, используя формулу полной вероятности, получаем.

P (A) = P (H₁) · P (A|H₁) + P (H₂) · P (A|H₂) + P (H₃) · P (A|H₃) == 0,25 · 0,9 + 0,35 · 0,8 + 0,4 · 0,7 = 0,815.

Ответ: 0,815.

Задание 4.

.

Дано распределение дискретной случайной величины X (табл.4). Найти математическое ожидание и среднее квадратичное отклонение.

Решение Математическое ожидание дискретной случайной величины находится по формуле.

Для нахождения дисперсии воспользуемся формулой:

Тогда среднеквадратическое отклонение равно.

Ответ: -0.3; 3.9.