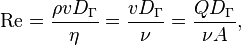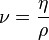Определение критерия подобия Рейнольдса

Число, или, правильнее, критерий Рейномльдса (), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса определяется следующим соотношением:

где.

— плотность среды, кг/м3;

— характерная скорость, м/с;

— гидравлический диаметр, м;

— динамическая вязкость среды, Па· с или кг/(м· с);

— кинематическая вязкость среды, м2/с ();

— объёмная скорость потока;

— площадь сечения трубы.

Для каждого вида течения существует критическое число Рейнольдса,, которое, как принято считать, определяет переход от ламинарного течения ктурбулентному. При течение происходит в ламинарном режиме, при возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, такими как изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Например, для течения (точнее, для стабилизированного изотермического потока) жидкости в прямой круглой[источник не указан 1362 дня] трубе с очень гладкими стенками. Для движения плёнки жидкости с относительно гладкой поверхностью раздела с газом при двухфазном потоке .

Значения Re выше критического и до определённого предела относятся к переходному (смешанному) режиму течения жидкости, когда турбулентное течение более вероятно, но ламинарное иногда тоже наблюдается — то есть неустойчивая турбулентность. Числу Reкр 2300 соответствует интервал 2300—10 000; для упомянутого примера с тонкими плёнками это 20−120 — 1600.

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, в водохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение. Напротив, возмущения потока могут значительно снижать величину .

Стоит отметить, что для газов Reкр достигается при значительно бомльших скоростях, чем у жидкостей, поскольку у первых куда больше кинематическая вязкость (в 10−15 раз).