Практика применения гамма-распределения в теории надежности технических систем

Для описания отказов системы могут быть предложены модели, предназначенные для решения различных задач надежности и по-разному учитывающие комплекс факторов, присущих характеру отказов.

Случайный характер возникновения отказов в процессе эксплуатации технических систем и их элементов позволяет применять в их описании вероятностно-статистические методы. Наиболее распространенными являются модели отказов, основанные на распределении соответствующих случайных величин — наработок до отказа невосстанавливаемых объектов и наработок между отказами восстанавливаемых объектов.

В качестве основных видов распределения наработок изделий до отказа следует выделить [1]:

• · экспоненциальное;
• · Вейбулла-Гнеденко;
• · гамма;
• · логарифмически-нормальное;
• · нормальное.

В результате обзора литературы в области надежности технических систем дана оценка практического применения гамма-распределения при исследовании различных технических объектов. На основе проведенного анализа можно подобрать подходящее априорное распределение соответствующего критерия или показателя надежности.

Гамма-распределение имеет двухпараметрическую плотность с параметром формы и параметром масштаба :

.

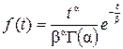
Вероятность безотказной работы определяется по формуле:

.

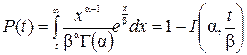
где — гамма-функция:

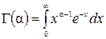
неполная гамма-функция:

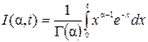
Математическое ожидание (среднее время безотказной работы) и среднее квадратическое отклонение для гамма-распределения равны:

;

.

Формула для интенсивности отказов следующая:

.

Гамма-распределение служит для описания износовых отказов; отказов вследствие накопления повреждений; описания наработки сложной технической системы с резервными элементами; распределения времени восстановления [2; 7−9]; а также может быть использовано при рассмотрении долговечности (ресурса) некоторых технических объектов [4].

Гамма-распределение обладает рядом полезных свойств:

• 1. При — интенсивность отказов монотонно убывает, что соответствует быстрому «выгоранию» ненадежных элементов.
• 2. При — интенсивность отказов возрастает, происходит постепенное изнашивание, старение элементов.
• 3. При — гамма-распределение совпадает с экспоненциальным и может быть использовано при описании вероятности появления отказов во время нормальной работы технической системы [5].

На основании вышесказанного можно сделать вывод, что гамма-распределение допустимо использовать на всех участках жизненного цикла: приработки (), нормальной эксплуатации () и старения () [10].

• 4. При — практически совпадает с нормальным распределением, поэтому может быть использовано при описании вероятности появления отказов стареющих узлов, механизмов и других элементов [2; 5]. Также при гамма-распределение сближается с нормальным законом распределения, по этой причине им часто приближают те одновершинные, но несимметричные распределения, которые плохо приближаются нормальным распределением [3; 6].
• 5. Если — целое положительное число, то в [8; 9] гамма-распределение также называется распределением Эрланга.

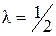
6. Если и кратно, то гамма-распределение совпадает с хи-квадрат распределением [8; 9].

Исходя из [7], в задачах, которые решаются в терминах преобразования Лапласа, гамма-распределением удобно аппроксимировать реальные распределения.

В [6] приводится следующее определение: гамма-распределение — характеристика времени возникновения отказов в сложных электромеханических системах в тех случаях, когда имеют место мгновенные отказы элементов на начальной стадии эксплуатации или в процессе отладки системы, то есть является удобной характеристикой времени возникновения отказов аппаратуры в процессе ее приработки.

Для сложных технических систем, состоящих из элементов, у которых вероятность безотказной работы имеет показательное распределение, вероятность безотказной работы системы в целом будет иметь гамма-распределение.

Распределение времени возникновения отказов сложной технической системы с резервом замещением (при условии, что потоки отказов основной системы и всех резервных простейшие) также может быть описано гамма-распределением [6]. Аналогичным образом в случае ненагруженного или смешанного резервирования вероятность безотказной работы системы подчиняется обобщенному гамма-распределению.

В заключение необходимо отметить, что при решении отдельных задач также применяют специальные виды (их несколько десятков), а также дискретные распределения, которые в рамках данной статьи не рассматривались. При этом между распределениями существуют различные взаимные переходы и связи. Несмотря на существующие критерии согласия выбранного теоретического и эмпирического распределения, они все дают ответ на вопрос: есть или нет достаточно серьезных оснований отвергнуть гипотезу о выбранном распределении? Авторами замечено, что любые данные можно подогнать под многопараметрический закон, даже если он не будет соответствовать реальным физическим явлениям [9]. Таким образом, при выборе вида распределения и его параметров необходимо прежде всего учитывать физическую сущность происходящих процессов и событий.

• 1. ГОСТ Р.27.001−2009. Надежность в технике. Модели отказов. — М.: Стандартинформ, 2010. — 16 с.
• 2. Герцбах И. Б., Кордонский Х. Б. Модели отказов / под ред. Б. В. Гнеденко. — М.: Советское радио, 1966. — 166 с.
• 3. Гнеденко Б. В. Вопросы математической теории надежности. — М.: Радио и связь, 1983. — 376 с.
• 4. Каштанов В. Н., Медведев А. И. Теория надежности сложных систем: уч. пособие — М.: ФИЗМАТЛИТ, 2010. — 609 с.
• 5. Литвиненко Р. С. Имитационная модель процесса функционирования электротехнического комплекса с учетом надежности его элементов // Журнал «Надежность». — 2016. — № 1 (56) — С. 46−54.
• 6. Литвиненко Р. С., Идиятуллин Р. Г., Киснеева Л. Н. Оценка надежности гибридного транспортного средства на этапе разработки // Журнал «Транспорт: наука, техника, управление». — 2016. — № 2 — С. 34−40.
• 7. Машиностроение: энциклопедия в 40 т. Т. IV-3: Надежность машин / В. В. Клюев, В. В. Болотин, Ф. Р. Соснин и др.; под общ. ред. В. В. Клюева. — М.: Машиностроение, 2003. — 592 с.
• 8. Труханов В. М. Надежность технических систем типа подвижных установок на этапе проектирования и испытания опытных образцов: научное издание — М.: Машиностроение, 2003. — 320 с.
• 9. Хазов Б. Ф., Дидусев Б. А. Справочник по расчету надежности машин на стадии проектирования. — М.: Машиностроение, 1986. — 224 с.
• 10. Черкесов Г. Н. Надежность аппаратно-программных комплексов: учеб. пособие. — СПб.: Питер, 2005. — 479 с.