Корреляционный анализ. 
Элементы высшей математики

Рассмотрим наиболее простой случай, когда фактор Х влияет на признак Y.

По данным парных экспериментальных замеров получаем корреляционную таблицу:

Для количественной оценки тесноты связи между Х и Y используют коэффициент корреляции:

Коэффициент R_xy принимает значения от -1 до +1.

Принято считать, что если.

|R_xy | < 0,3, то корреляционная связь слабая,.

|R_Xy| = 0,3 0,7 — средняя,.

0,7 < R_xy < 1, то корреляционная связь сильная.

При коэффициенте корреляции R_xy > 0 возрастание Х приводит к росту и Y и, наоборот, уменьшение значений Х приводит к снижению значений и Y.

Если же R_Xy < 0, то изменение Х в одну сторону приводит к противоположному изменению Y.

Если на признак Y действует несколько факторов, то рассматривают тесноту связи между изменениями всех факторов Х_ЬХ₂,…, Х_п и изменениями Y.

Регрессионный анализ

Регрессионный анализ предназначен для представления влияния факторов X1, Х2,., Х_п на признак Y в виде уравнения регрессии:

У = f (x_b x2,…, xn). (5.35).

В случае парной корреляции, т. е. влияния одного фактора Х на признак Y, уравнение регрессии выбирают в виде:

у = а₀ + a₁x, или у = а₀ + a₁x + a₂ x, или (5.36).

у = а₀ * EXP (a₁x).

В случае множественной линейной регрессии в качестве модели выбирают уравнение вида:

у = а0 + arx! + a2² +… + an^. (5.37).

Для определения неизвестных коэффициентов а0 или ai применяют метод наименьших квадратов (МНК).

Согласно этому методу, коэффициенты а₀ и a_i должны быть выбраны такими, чтобы обеспечить наименьшее значение суммы квадратов отклонений теоретических значений уравнения регрессии от экспериментальных, выбранных из корреляционной таблицы. То есть требуется выполнение условия:

I[f (xi, a0, a₁)-yj = mm. (5.38).

Графически отклонения теоретических значений признака от его замеров в случае линейной модели регрессии можно представить следующим образом (рис. 5.7).

Обозначим через.

h_i = [ f (x_i, a₀, a₁) — y_i ].

Тогда условие (5.38) запишем в виде:

h₁² + h₂² +… + h_n ² = min. (5.39).

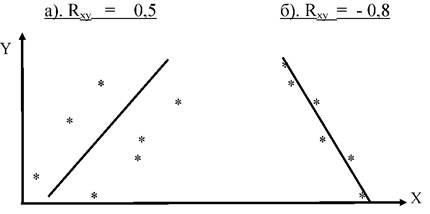
Рис. 5.7 Геометрическая интерпретация МНК

Рассмотрим применение МНК для определения неизвестных коэффициентов а₀ и a₁ в случае выбора линейной модели уравнения регрессии: у = а₀ + ai-x.

Запишем функционал (5.38) для случая линейной модели:

F (ao, a,) = ^ (ao + a,-Xi — Yi) = min (5.40).

Для определения минимального значения функционала F (a₀, a₁) необходимо приравнять его частные производные по переменным а₀ и а₁ к нулю.

В результате получаем:

Отсюда получаем систему линейных уравнений для определения неизвестных коэффициентов а₀ и a₁:

Замечание Если R_xy > 0 (или R_xy < 0), то в случае построения линейного регрессионного уравнения у = а + Ьх его график может иметь вид.

ПРИМЕР 1.

Выработка бригады (Y) зависит от ее численности (X) согласно следующей таблице:

Определить коэффициент корреляции R^ между этими случайными величинами и построить линейное уравнение регрессии.

Решение.

По формулам (5.30), (5.31) находим: х = 4,5; у = 22,6;

Окончательно, R ху = ^ ₅ ⁼ °,⁸⁸.

Cледовательно, между Х и Y — сильная корреляционная связь.

Далее для определения коэффициентов, а и b в выбранном линейном регрессионном уравнении:

у=а+ bx воспользуемся формулами (5.42).

В результате получаем:

8 а + 36 b =181 36 а + 204 b = 1024.

В результате решения этой системы находим, а «0, b В результате регрессионное уравнение примет вид: у = 5-х.

ПРИМЕР 2.

Характеризовать степень влияния СВ Х на СВ Y, если коэффициент корреляции между ними равен:

а). = 0,5 б). = - 0,8.

Изобразить графически линейные уравнения связи y=f (x) и примерное расположение экспериментальных точек для обоих случаев.

Решение.

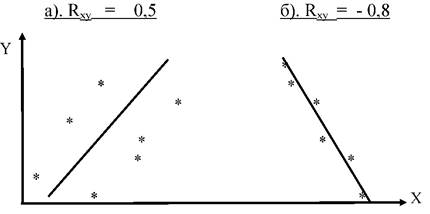
ПРИМЕР 3.

Бригада из N тракторов за некоторое время Т вспахивает поле. Оценить коэффициент корреляции R_NT.

Решение Заметим, что при увеличении числа N тракторов время Т выполнения работы будет снижаться, т. е. R_NT < 0.

Если тракторы одинаковой марки и работники одинаковой квалификации, то R_NT = - 0,8 ^ (- 0,9).

Если тракторы разных марок, то возможен разброс в производительности труда трактористов, нарушается пропорциональность их вклада в общий объем работы и R_NT = - 0,7 ^ (- 0,8).

ПРИМЕР 4.

Автосалон за первые 8 месяцев года (Т= 1,2,3,4,5,6,7,8) продал соответственно N = 54, 56, 57, 59, 62, 64, 66, 68 машин. Оценить (не считая) коэффициент корреляции RTN.

Решение Если бы прирост продаж машин был бы строго пропорциональным (т.е. увеличивался каждый месяц ровно на 2 машины), то RTN = 1.

Однако в марте (Т=3) и в мае (Т = 5) произошло изменение этой строгой пропорциональности (прирост составил 1 и 3 машины).

Вследствие незначительного нарушения этой пропорциональности можно предположить, что коэффициент корреляции составит R_tn = 0,85 — 0,95.

Больший разброс в числах реализации машин по месяцам приводит к снижению (по абсолютной величине) коэффициента корреляции RTN.

ЗАДАНИЕ.

1). На метеорологической станции проводились замеры температуры Т за некоторый период времени прошлого года:

Определить вероятность Р, что в этом году в этот же период времени Т будет находиться в пределах 18 < T < 21 C.

2). На полигоне проводились замеры скорости V новой модели трактора:

Определить вероятность Р, что на основных испытаниях этот трактор покажет скорость в пределах 48 < V < 54 км/ч.

3). В результате статистических исследований производительности труда n = 36 рабочих цеха установлено, что один рабочий в среднем выпускает в смену р = 50 деталей.

Разброс числа выпускаемых деталей одним рабочим характеризуется дисперсией а² = 64 (дет.)². Найти с вероятностью да = 0,95 доверительный интервал для математического ожидания М (р) производительности труда рабочих цеха.

4). Определить коэффициент корреляции R_xy и построить уравнение регрессии между случайными величинами Х и Y, заданными таблицей:

• 5). Грузовой машине требуется за несколько рейсов доставить груз со склада на станцию. Оценить (не считая) коэффициенты корреляции: а). R_rN между грузоподъемностью машины Г и количества необходимых рейсов N; b). RLN между Г и длиной L маршрута от склада до станции.
• 6).Характеризовать степень влияния случайной величины Х на случайную величину Y, если коэффициенты корреляции между ними: а). R_xy = - 0,5 b) R_xy = 0,9.

Представить графически линейные уравнения регрессии y = a + bx для обоих случаев а) и b) и примерное расположение точек экспериментальных замеров на графике.

• 7). Характеризовать степень влияния случайной величины Х на случайную величину Y, если коэффициенты корреляции между ними:
  • а). R_xy = - 0,9 b) R_xy = 0,5.

Представить графически уравнения регрессии (параболы).

y = a + bx для обоих случаев а) и b) и примерное расположение точек экспериментальных замеров на графике.

8). Утеряны некоторые результаты замеров зависимости случайной величины Y от случайной величины Х.

Восстановить (примерно) значения y₂, y₃, y₄, y₅, y₆: если коэффициент корреляции между Х и Y равен: а). Rxy = 0,6 b) Rxy = - 0,9.

8). Утеряны некоторые результаты замеров зависимости случайной величины Y от случайной величины Х.

Восстановить (примерно) значения y2, y3, y4, y5, y6: если коэффициент корреляции между Х и Y равен: а). Rxy = 0,9 b) Rxy = - 0,6.